В наших работах [2, 6] изучено явление распада мультикритической точки для случая термодинамического потенциала, инвариантного относительно группы преобразований 3m (C3v). Это явление впервые было теоретически исследовано в [3]. Термодинамический потенциал с такой симметрией описывает структурные фазовые превращения в некоторых интерметаллидах, пероксидах, шпинелях, гранатах и т.д.
Симметрия потенциала, представляемого в виде разложения шестой степени по компонентам параметра порядка η:
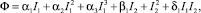(1)
где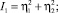 
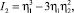обуславливает существование на фазовой диаграмме нескольких симметрийно неэквивалентных типов фаз: высокосимметричная фаза I (η1, η2 = 0), однопараметрические фазы II (η1 < 0, η2 = 0) и III (η1 > 0, η2 = 0), двухпараметрическая фаза IV (η1, η2 ≠ 0) [3].
Целью работы является исследование возможности существования на фазовой диаграмме для данного типа потенциала изосимметрийных модификаций однопараметрических фаз.
Условия существования изоструктурных фаз
Рассмотрим уравнение состояния однопараметрических фаз:
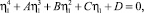(2)
где
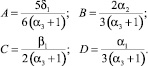
Нас интересуют только те из корней уравнения (2), которые удовлетворяют двум условиям термодинамической устойчивости, т.е. достаточным условиям минимума потенциала (1):
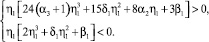
Уравнение состояния (2) может иметь два или четыре действительных корня или не иметь их вовсе. Для существования нескольких изосимметрийных однопараметрических модификаций уравнение (2) должно иметь несколько корней одного знака. Если, однако, оно имеет только два корня одного знака, то эти корни не могут одновременно отвечать устойчивым модификациям, ибо в этом случае один из корней соответствует максимуму, а не минимуму термодинамического потенциала (1). Для существования двух устойчивых (согласно первому условию устойчивости) модификаций одной и той же однопараметрической фазы нужно, чтобы уравнение (2) имело не менее трёх корней одного знака, а общее число его корней должно быть равно четырём. Однако и этих условий оказывается недостаточно. Можно показать, что если имеется только три корня одного знака, то для выполнения первого условия устойчивости для двух из них нужно потребовать выполнения условия α1 < 0.
Итак, необходимыми условиями существования изосимметрийных однопараметрических фаз являются следующие требования:
1) уравнение (2) должно иметь четыре действительных корня;
2) не менее трёх корней из них должны иметь одинаковый знак;
3) если имеется только три корня одного знака, то должно быть также α1 < 0.
Эти условия не являются достаточными, ибо не учитывают второе условие устойчивости, которое, как показали компьютерные расчеты, в ряде случаев вносит лишь незначительные коррективы в форму искомых областей.
Используя три перечисленных выше условия и теорему Штурма, можно показать, что область сосуществования двух удовлетворяющих первому условию устойчивости модификаций фазы типа II возникает, если
E, H, J > 0, N = 0
или
E, H, J > 0, N = 1, α1 < 0.
Аналогично для фазы III:
E, H, J > 0, N = 4
или
E, H, J > 0, N = 3, α1 < 0.
Здесь N – число перемен знака в ряду величин D, C, G, I, J, и
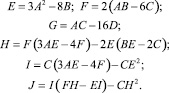
Примеры расчётных фазовых диаграмм с изоструктурными модификациями
Приведём несколько примеров. На рис. 1 показана фазовая диаграмма (построенная в координатах коэффициентов модельного потенциала α1 и β1, являющихся в теории Ландау линейными функциями обычных интенсивных термодинамических параметров), где сплошными линиями обозначены границы областей устойчивости фаз, а мелким пунктиром – линии фазовых переходов первого рода. Крупным пунктиром обозначена граница области одновременной устойчивости двух модификаций фазы II. В этой области уравнение (2) имеет три отрицательных корня и один положительный. Двум «сериям» отрицательных корней, удовлетворяющим условиям устойчивости, можно поставить в соответствие различные модификации фазы II: меньший по модулю корень можно условиться относить к модификации IIa, а больший – к модификации IIb. Прямая линия в этой области, проведённая мелким пунктиром, обозначает равновесие между двумя модификациями. Например, при β1 = 0 равновесие достигается при α1,eq = –2,0645. Если α1 < α1,eq, то более устойчивой (т.е. отвечающей наиболее глубокому минимуму потенциала) является фаза IIb, если же α1 > α1,eq, то наиболее устойчива фаза IIa. В сечении η2 = 0 при «равновесном» значении α1 = α1,eq два минимума потенциала Φ = f(η1), соответствующие двум модификациям фазы II, имеют одинаковую глубину, а при других значениях α1 один из минимумов – более глубокий и соответствует более устойчивой модификации.
Изменив коэффициент δ1, получим другую диаграмму (рис. 2). Здесь также имеется область, где фаза II может быть в виде двух модификаций, но теперь она частично принадлежит области «II + III», в которой пунктиром проведена линия равновесия между фазой III и наиболее устойчивой модификацией фазы II. Эта линия совпадает с линией равновесия между двумя модификациями фазы II, так что здесь мы имеем дело с трёхфазным равновесием: на этой линии совпадают термодинамические потенциалы фаз IIa, IIb и III.
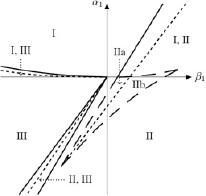
Рис. 1. Возникновение областей сосуществования нескольких модификаций фазы II. Случай α2 = 8, α3 = 1, δ1 = 7,7
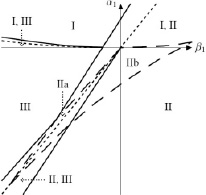
Рис. 2. Возникновение областей сосуществования нескольких модификаций фазы II. Случай α2 = 8, α3 = 1, δ1 = 8
Вопрос об изоструктурных фазовых переходах для рассматриваемого модельного потенциала (1) ранее затрагивался в работе [1], где, однако, не было указано на возможность существования описанной нами непрерывной линии трёхфазного равновесия.
Заключение
В заключение отметим, что фазовые диаграммы с областями сосуществования изосимметрийных однопараметрических фаз могут быть экспериментально получены для различных классов кристаллов. В случае кристаллов со структурой шпинели (пространственная группа Fd3m) структуры однопараметрических фаз имеют тетрагональную симметрию (пространственная группа I41/amd) [4, 5, 7]. В работе [8] экспериментально доказано существование прогнозируемых изосимметрийных тетрагональных модификаций шпинелей.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.
Рецензенты:
Денисов В.В., д.т.н., профессор, зав. кафедрой ЭТЭПиР Южно-Российского государственного технического университета, г. Новочеркасск;
Зубехин А.П., д.т.н., профессор кафедры ТКСиВВ Южно-Российского государственного технического университета, г. Новочеркасск.
Работа поступила в редакцию 08.05.2013.