Выяснение природы формирования термодинамических свойств кристаллической решетки трансурановых металлов имеет принципиально важное научное и практическое значение. При этом имеющаяся экспериментальная информация об этих свойствах явно недостаточна. Так, экспериментальные данные о коэффициенте теплового расширения (КТР) и модуле всестороннего сжатия америция (МВС) ограничены по значениям температуры и известны только для изотопа 243Am [5, 9, 7]. Та же ситуации наблюдается и для нептуния [6, 8, 10], для которого известны значения модуля всестороннего сжатия при T = 77 K (129,4 ГПа) и T = 289 K (112,0 ГПа) [8], а объёмный коэффициент теплового расширения был определен в интервале температур от 100 до 500 K [3]. Более разнообразны и обширны данные по α- и δ-плутонию. В литературе представлены теплофизические параметры этих веществ в широком интервале температур (от гелиевых температур до температур плавления) [4]. Кюрий также является малоизученным металлом, для которого экспериментальных значений по МВС практически нет, а данные по КТР ограничены двумя значениями для T = 195 K (3,58∙10–6 K–1) и T = 300 K [11].
В связи с этим представляет интерес моделирование теплофизических свойств трансурановых актинидов, которое позволяет прогнозировать оценочные значения рассматриваемых свойств исследуемых металлов, а также определять возможную роль в формировании теплофизических свойств их фононной подсистемы.
При построении термодинамической модели для описания решеточных составляющих свойств трансурановых актинидов следует учитывать возможное влияние на них фононного ангармонизма. Ангармонизм фононов существенным образом влияет на температурные зависимости термодинамических функций, особенно в области повышенных температур, и может привести к ряду эффектов, не находящих объяснения в рамках теории Дебая−Грюнайзена.
Молярный термодинамический потенциал (ТДП) Гиббса в рамках рассматриваемой модели представляется в виде суммы Φ = Φ0 + Φph + Φel, здесь Ф0 – «постоянная» часть потенциала, не зависящая от температуры; Фрh = Фрh(θ,T) – фононная часть ТДП, описываемая выражением [12]:
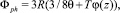(1)
в котором T – температура, θ – температура Дебая, z = θ/T, φ(z) = ln(1 – e–z) – D(z)/3, а D(z) – стандартная функция Дебая; Фel = Фel(T) – составляющая ТДП, связанная с электронной подсистемой.
Кроме того, в соответствии с (1) имеем следующее выражение для решеточной составляющей теплоемкости:
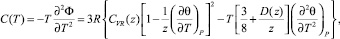(2)
где CVR(z) – стандартная дебаевская теплоемкость, нормированная на 3R, D(z) – функция Дебая, а температура Дебая, вообще говоря, зависит от внешней температуры.
Выражения для линейного коэффициента α теплового расширения (ЛКТР) и модуля K всестороннего сжатия (МВС), получаемые в таком подходе на основе фононного вклада ТДП (1), имеют вид:
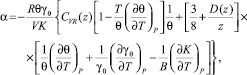(3)
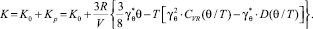(4)
Входящие в (3) и (4) параметры γq и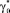 
представляют собой обобщенные параметры Грюнайзена, а температура Дебая рассчитывается по формуле:
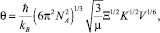(5)
где m – молярная масса; K – модуль всестороннего сжатия (МВС); V – молярный объем; ħ, kB, NA – постоянные Планка, Больцмана и Авогадро, а Ξ – вспомогательная функция, зависящая от коэффициента Пуассона σ, который характеризует отношение модуля сдвига G к модулю всестороннего сжатия K.
Для устранения принципиальных внутренних противоречий дебаевской модели в ее традиционной интерпретации эффективной является самосогласованная итерационная схема расчета термодинамических характеристик, которая может быть реализована численно методом последовательных приближений. Учет не идеальности фононного спектра выражается через значение θ(T) в рамках обобщенной модели Дебая [2].
Этапы вычисления состоят из ряда приближений: затравочного, нулевого, первого и последующих. Для проведения затравочных расчетов задаются начальные значения термодинамических параметров, которые впоследствии будут варьироваться: V0, K0, γq,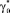 
. Строго говоря, ни один из параметров не является свободным, так как они могут быть измерены. Это позволяет вычислить затравочные значения усредненной и парциальных температур Дебая θ0, θ01, θ0t, плотности ρ0, усредненных значений обобщенных γθ0 – параметров Грюнайзена.
В нулевом приближении (n = 0) вычисленные затравочные значения указанных выше параметров позволяют провести полноценное вычисление в приближении постоянства температуры Дебая θ = θ(T), температурных зависимостей V(T), K(Т), ρ(Т) в выбранном узком интервале температур вблизи комнатной температуры. Исходя из этого, становится возможным вычисление температурных зависимостей θ(T), θl(T), θt(T), а также соответствующих температурных производных. Затем вычисляются усредненные значения γq – параметров Грюнайзена, откуда определяются оставшиеся термодинамические параметры С(Т) и α(Т) в данном приближении.
В первом и последующих приближениях (n = 1, 2,...) расчеты организуются таким же образом, как и в нулевом приближении, с той лишь разницей, что счет ведется с учетом зависимости θ(T). Итерационный самосогласующийся процесс может быть прерван по некоторому произвольно заданному условию, например, после того, как разница в величине θ в двух последовательных приближениях становится менее 0,01 K. Как показывают расчеты, для этого достаточно первых трех-пяти приближений [1].
Организовав описанным выше образом итерационный процесс, программно варьируя затравочные параметры и добиваясь наименьшего среднеквадратичного отклонения между имеющимися экспериментальными данными и соответствующими расчетными значениями термодинамических параметров, можно получить взаимосогласованные значения всего комплекса физических величин, определяющих термодинамику исследуемого твердого тела. Важно отметить, что ввиду самосогласованности выполняемых расчетов может использоваться весь имеющийся набор точек.
В таблице приведены значения фононной составляющей теплоёмкости, линейного коэффициента теплового расширения (ЛКТР), модуля всестороннего сжатия (МВС), плотности и обобщённого параметра Грюнайзена при T = 300 K, в скобках указано экспериментальное значение для данных трансурановых актинидов для той же температуры. Необходимо отметить, что обобщенный параметр Грюнайзена первого порядка для температуры Дебая gθ с точностью до знака совпадает с известным параметром Грюнайзена твердого тела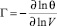 
, характеризующего степень ангармоничности решеточных колебаний.
|
C300, Дж∙К–1∙моль–1 |
α300∙10–6, К–1 |
K300, ГПа |
ρ300, кг∙м–3 |
Γ300 |
Γ300∙α300∙10–6, К–1 |
|
|
Ph (Exp) |
Ph (Exp) |
Ph (Exp) |
Ph (Exp) |
|||
|
Np |
27,04 (29,67) |
20,52 (21,31) |
118,27 (112,00) |
20380 (20378) |
2,77 |
56,66 |
|
α-Pu |
31,73 (33,86) |
65,98 (52,51) |
53,00 (53,96) |
19475 (19704) |
5,22 |
344,42 |
|
δ-Pu |
26,69 (30,63) |
10,28 (7,44) |
33,78 (31,19) |
15572 (15590) |
0,67 |
6,47 |
|
Am |
25,11 (25,50) |
6,67 (7,27) |
35,99 (36,10) |
13667 (13671) |
0,51 |
3,40 |
|
Cm |
25,02 (28,60) |
9,35 (10,07) |
34,19 (34,20) |
13584 (13460) |
0,71 |
6,64 |
Роль ангармонизма в теплоёмкости очень существенна, что можно проследить на примере α-плутония. Фононная составляющая без учёта ангармонизма составляет 24,58 Дж∙моль–1∙K–1. Считая обобщённый параметр Γ300∙α300 обобщённой мерой ангармонизма, можно видеть, что в случае α-плутония данный параметр достигает максимального значения, равного 344,42∙10–6 K–1.
С ангармонизмом решетки и особенностями упругих свойств δ-плутония тесно связана его решеточная теплоемкость. Однако ранее для выделения решеточных вкладов в теплоемкость в основном использовались либо классическая модель Дебая, например, либо квазигармоническое приближение с учетом данных по неупругому рассеянию нейтронов и измерению скорости звука в случае сплавов Pu0.95Al0.05 [4]. Фононный ангармонизм здесь также обусловливает повышенное значение коэффициента теплового расширения и модуля всестороннего сжатия нептуния [3], что видно из таблицы.
Согласно проведенным оценкам температурных зависимостей ЛКТР и МВС, для америция характерен относительно слабый (по сравнению с нептунием и плутонием) решеточный ангармонизм. Это согласуется с наблюдаемым вкладом фононного ангармонизма в теплоемкость и подтверждается достаточно низким значением решеточного параметра Грюнайзена америция, который, согласно выполненным расчетам при температуре T = 300 K, не превышает 0,51. Тот же вывод можно сделать и для кюрия, хотя параметра Грюнайзена при T = 300 K здесь составляет 0,71.
Таким образом, в настоящей работе выполнен самосогласованный анализ термодинамических свойств трансурановых элементов на примере Np, α-Pu, δ-Pu, Am, Cm с учетом решеточного ангармонизма. Одной из важных причин формирования ангармонизма являются дефекты кристаллической решетки, возникающие вследствие радиоактивного распада трансурановых элементов. Отдельной важной задачей также является исследование электронных вкладов в теплофизические свойства рассматриваемых веществ, особенно в области низких (по сравнению с температурой Дебая) температур.
Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.А18.21.0737.
Рецензенты:
Чикова О.А., д.ф.-м.н., профессор, зав. кафедрой технологии, ФГБОУ ВПО «Уральский государственный педагогический университет», г. Екатеринбург;
Сидоренко Ф.А., д.ф.-м.н., профессор кафедры физики, ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 18.06.2013.