В современных условиях назрела необходимость формирования качественно новых методических подходов оценки эффективности инвестиций, учитывающих риски, а также неполноту и/или неточность исходной информации.
В настоящее время существуют различные подходы к оценке рисков. Особый интерес представляет теория нечеткой логики (fuzzy logic), определяющая современный подход к описанию бизнес-процессов, в которых присутствуют неопределенность и неточность исходной информации. Процесс принятия решений в этом случае имеет многоаспектный и чрезвычайно сложный характер и требует привлечения современного программного обеспечения.
В данной работе предлагается двухэтапный метод оценки эффективности инвестиций. На первом этапе характеристики инвестиционного проекта оцениваются с помощью программного обеспечения для разработки бизнес-планов, например, Project Expert [6]. Затем полученные характеристики рассматриваются как входные данные оценки эффективности на основе нечеткой логики [2]. В качестве алгоритма нечеткой логики выбран алгоритм Мамдани [1].
В качестве конкретного проекта выбран проект внедрения передвижных отделений почтовой связи в Козельском районе Калужской области [5].
Характеристики нечетких множеств и функций принадлежности
В основе формализма нечеткой логики [7] лежат понятия нечетких множеств, нечетких высказываний и т.п. Для анализа нечетких высказываний разработана нечеткая логика, методы которой относятся к так называемым мягким вычислениям, основанным на вероятностном подходе.
В нечеткой логике также существует понятие нечеткой функции и разработана концепция построения нечетких регрессионных моделей. В рамках такого подхода было введено понятие нечеткой лингвистической переменной, значения которой могут быть выражены в терминах типа «низкая», «умеренная», «большая», «очень высокая» и т.п.
Множество значений нечеткой переменной образуют так называемое терм-множество. Например, переменная «Уровень фактора» при осуществлении комплексной оценки риска банкротства предприятия может обладать терм-множеством значений {«Очень низкий», «Низкий», «Средний», «Высокий», «Очень высокий»}.
В случае четкой (обычной) логики и четких множеств, определенных на некотором универсальном множестве U, о каждом элементе универсального множества можно сказать, принадлежит ли он рассматриваемому четкому множеству Х. Таким образом, можно определить функцию принадлежности множеству Х, которая принимает значение 1, если элемент принадлежит множеству, и ноль – в противном случае. В случае нечеткой логики функция принадлежности принимает значения на отрезке [0; 1] и задает вероятность события, что элементы универсального множества принадлежат заданному нечеткому множеству А.
В данной работе мы рассматривали следующие нечеткие переменные. В качестве входных использовались чистая текущая стоимость (NPV), внутренняя норма рентабельности (IRR), срок окупаемости проекта (РВ), учетная норма рентабельности (ARR), индекс рентабельности инвестиций (PI). Значение выходной переменной определяло вероятность принятия проекта.
Одной из основных проблем применения нечеткой логики является выбор функций принадлежности нечетких переменных. Основными видами функций принадлежности являются треугольные, трапециевидные, кусочно-линейные, гауссовы, сигмоидные и другие функции. Переменные NPV и ARR характеризовались терм-множеством значений {«низкое» (low), «среднее» (mid) и «высокое» (high)} и описывались трапециевидными функциями принадлежности. Для переменной PI было выбрано терм-множество значений {«низкое» (low) и «высокое» (high)} с гауссовыми функциями принадлежности (рис. 1). Переменные PB и ARR для проектов со сроком окупаемости менее пяти лет или нормой рентабельности более 20 % имели логическое значение «да» (yes), в противном случае ‒ логическое значение «нет» (no).
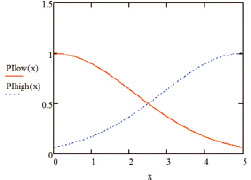
Рис. 1. Функции принадлежности выходной переменной
Переменные PB и ARR для проектов со сроком окупаемости менее пяти лет или нормой рентабельности более 20 % имели логическое значение «да» (yes), в противном случае – логическое значение «нет» (no).
Алгоритм нечеткого вывода
Говоря о нечеткой логике, чаще всего имеют в виду системы нечеткого вывода, которые лежат в основе различных экспертных и управляющих систем
Остановимся на основных этапах нечеткого вывода.
1. Фазификация (определение значений) входных переменных.
Задаются четкие значения входных переменных.
2. Агрегирование (композиция). На этом этапе строятся усеченные функции принадлежности переменной вывода, которые объединяются, чтобы формировать одно нечеткое множество. Пример построения усеченных функций принадлежности для четкого значения одной из переменных показан на рис. 2. Функция принадлежности входной переменной обозначена как f1(x). Четкое значение входной переменной равно шести. Подобное построение проводится для каждой входной переменной.
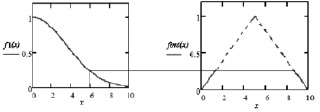
Рис. 2. Построение усеченной функции принадлежности
Затем строится итоговое нечеткое множество для выходной переменной. В алгоритме Мамдани объединение усеченных функций принадлежности переменной вывода производится с использованием операции МАКСИМУМ, если соответствующее правило соответствует логическому ИЛИ, и с использованием операции МИНИМУМ, если соответствующее правило соответствует логическому И.
3. Формирование базы правил (базы знаний).
В нашей работе мы рассмотрели два варианта задания базы правил. В первом варианте считались допустимыми все проекты с положительным значением чистой приведенной стоимости:
• если NPV или IR низкий, то результат низкий;
• если NPV средний, IRR средний, PB = «yes», AR = «yes» и PI – высокий, то результат средний;
• отвергаются проекты со сроком окупаемости более трех лет или учетной нормой рентабельности менее 20 %. Здесь возможны два варианта:
1) данные проекты отвергаются в процессе предварительного анализа и не обрабатываются на основе нечеткой логики;
2) для переменных РВ и ARR задаются «ступенчатые» функции принадлежности, которые равны нулю на соответствующих интервалах;
• если PB и ARR имеют логическое значение «да» и PI – высокий, то результат высокий.
Во втором варианте последнее правило имело вид:
• если NPV высокий, а PB и ARR имеют значение «да» и PI – высокий, то результат высокий.
Очевидно, что первый вариант является более «мягким», а второй – более «жестким».
4. Дефазификация. На этом этапе нечеткий набор выводов преобразуется в четкое число, например с применением центроидного метода, когда результат является х-координатой центра тяжести фигуры, полученной на этапе 3.
Примеры вычислений
Средой реализации нечетких вычислений по алгоритму Мамдани был выбран пакет прикладных программ Mathcad. Достоинством пакета является его простота, доступность, множество вариантов лицензирования [3], а также возможность реализации решения задач в виде облачных вычислений [4].
В качестве входных параметров возьмем данные, соответствующие оценке проекта внедрения передвижных отделений почтовой связи в Козельском районе, полученные как выходные данные программы ProjectExpert[5]: NPV = 2200 тыс. руб., IRR = 15; PB = 1,5; ARR = 37; PI = 1,12.
Пример вычислений по алгоритму Мамдани показан на рис. 3. В данном случае очевидно, что вероятность эффективной реализации проекта достаточно высока (~76 % по «жесткому» и ~78 % по «мягкому» варианту).
При оценке результата проекта необходимо учитывать различные варианты развития событий, т.е. проводить разработку сценариев реализации проектов в наиболее вероятных или наиболее «опасных» для каких-либо участников условиях и давать оценку финансовых последствий осуществления таких сценариев. Для оценки эффективности инновационного проекта внедрения ПОПС в качестве одного из вариантов рассматривался «пессимистический» вариант развития, когда доходная часть бюджета остается неизменной, а расходная часть изменяется в зависимости от внешних и внутренних факторов. Наши расчеты показывают, что в этом случае для того, чтобы ожидаемая вероятность эффективности проекта превысила 50 %, значение NPV должно быть не ниже 1400 тыс. руб.
Выводы
В работе предложен двухэтапный метод оценки эффективности инвестиционных проектов, основанный на применении соответствующего программного обеспечения (Project Expert) и формализма нечеткой логики. На первом этапе вычисляются характеристики проекта (чистая приведенная стоимость NPV, внутренняя норма рентабельности IRR, срок окупаемости PB, учетная норма рентабельности ARR, индекс рентабельности инвестиций PI). На втором этапе эти значения используются как входные переменные программы оценки эффективности инвестиций методами нечеткой логики. В качестве алгоритма нечеткой логики использовался алгоритм Мамдани.
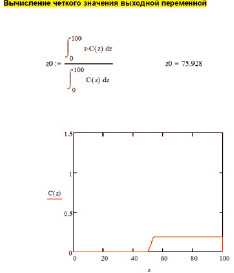
Рис. 3. Пример вычислений по алгоритму Мамдани
Разработанная методика была применена к оценке эффективности проекта внедрения передвижных отделений почтовой связи и показана высокая эффективность проекта в рассмотренных ранее вариантах задания базы правил.
Данная работа в области разработки методов оценки эффективности инвестиций поддержана РГНФ и администрацией Калужской области (грант № 13-12-40013).
Рецензенты:
Черняев С.И., д.т.н., профессор кафедры «Менеджмент и маркетинг» Калужского филиала ГОУ ВПО «Финансовый университет при правительстве Российской Федерации», г. Калуга;
Круглов В.Н., д.э.н., профессор кафедры «Экономика и финансы» Калужского филиала ГОУ ВПО «Финансовый университет при правительстве Российской Федерации», г. Калуга.
Работа поступила в редакцию 18.06.2013.



