Использование в высокоскоростных роторных системах подшипников на газовой смазке связано с необходимостью практической реализации прорывных технологий, например, в ситуациях, когда применение газовых опор является единственно возможным решением, обеспечивающим нормальную работу узлов трения. Известно успешное применение газовых подшипников в станкостроении [1, 4, 5, 7], криогенной и авиакосмической технике, метрологическом оборудовании, гироскопических устройствах, газотурбинных установках, в атомной энергетике и т.д. При этом следует указать на достаточно ограниченную информацию о реальном внедрении газовых опор в различные механизмы, что связано с коммерческой и оборонной секретностью.
К настоящему времени заложены хорошие основы расчета эксплуатационных характеристик газовых подшипников, которые в целом говорят о надежных результатах, получаемых с применением численных методов [3, 6, 10]. Между тем результаты исследования, представленные в работах [8, 9], показывают на вполне удовлетворительное согласование опытных и теоретических результатов, полученных на основе аналитической методики расчета с использованием разложением по малому параметру, в качестве которого принято число сжимаемости. Однако с ростом числа сжимаемости (больше 0,4) наблюдается заметное рассогласование теоретических и экспериментальных данных.
С целью расширения сведений о характеристиках подшипников, работающих в широком диапазоне изменения числа сжимаемости, в КнАГТУ разработана аналитическая методика расчета, в основе которой лежит метод разложения по малому параметру, в качестве которого принят относительный эксцентриситет. Эта методика и излагается в настоящей работе.
Пусть газ из камеры нагнетания под давлением Ps поступает через пористые вставки в смазочный слой цилиндрического подшипника. Пористые вставки расположены равномерно по окружности в два ряда. Форма пористых вставок цилиндрическая. На вал действует внешняя радиальная нагрузка F (рис. 1).
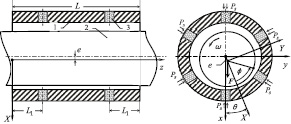
Рис. 1. Газовый статический подшипник с двумя рядами пористых вставок:1 – непроницаемая часть вкладыша подшипника; 2 – вал; 3 – пористая вставка
Используя общепринятые допущения [2], получим уравнения для определения поля давления в зазоре: в непроницаемой части вкладыша подшипника
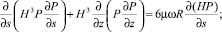(1)
в пористой среде
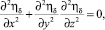(2)
где s = φR – длина дуги в смазочном слое; R – радиус вала; φ – полярный угол, отмеряемый от линии действия нагрузки (сечение с максимальным давлением); H – толщина смазочного слоя, H = c(1 – εcos φ); с – средний радиальный зазор, ε = e/c – относительный эксцентриситет; e – эксцентриситет; P = P(s, z) – абсолютное давление в смазочном слое подшипника,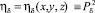 
– квадрат давления в пористой среде (здесь и далее индекс δ означает характеристики пористой среды); μ – коэффициент вязкости; ω – угловая скорость вращения вала; L = 2L0 – длина подшипника.
При работе подшипника в режиме подвеса (ω = 0, θ = 0) ряды пористых вставок в первом приближении заменим эквивалентными им по площади пористыми кольцевыми втулками шириной Δ (метод непрерывных линий наддува). В работе [8] найдено приближенное решение системы уравнений (1), (2) и определены наибольший и наименьший квадрат давления в области пористых вставок:
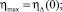
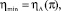
где
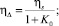
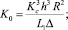
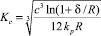
– конструктивный параметр, h = H/c, h = 1 – εcos φ – относительная толщина смазочного слоя.
Переходя в уравнении (1) к безразмерным переменным, получаем
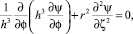(3)
где ζ = z/L0;, ζ ∈ [0, 1], ψ = η/Δη – относительный квадрат давления, Δη = ηmax – ηmin, r = R/L0 – относительный радиус вала.
Решение уравнения (3) найдем в виде ψ(φ, ζ) = X(φ)Z(ζ). Подставляя эту функцию в уравнение и разделяя переменные, получим систему уравнений:
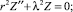(4)
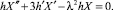(5)
Из уравнения (4) находим:
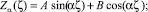
α = λ/r; λ ≠ 0; (6)
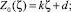λ = 0. (7)
Решения уравнения (5), соответствующие (6) и (7), обозначим: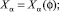 
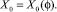Таким образом, решение уравнение (3) представляется в виде
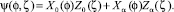(8)
Решение уравнения (5) при λ ≠ 0 было найдено в работе [9] в виде ряда по степеням τ = cos φ, но этот ряд медленно сходится и распределение давления в сечениях ζ = const существенно зависит от числа слагаемых в приближенном решении.
В связи с этим зависимость h = h(φ) заменим линейной
h0 = h0 (φ),
где
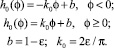
В полученное решение подставим h = h(φ), что равносильно замене производной h′ в уравнении (5) ее средним значением ⟨h′⟩.
В этом случае при λ = 0 нормированное решение, удовлетворяющее условиям: X0(0) = 1, X0(π) = 0, будет иметь
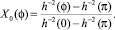
При λ ≠ 0 после перехода к новой независимой переменной
τ = (1 + cos φ)/2, τ ∈ [0, 1],
h = (1 + ε)(1 – k1τ), k1 = 2ε/(1 + ε),
получим:
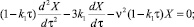
ν = πλ. (9)
Решение последнего уравнения будем искать в виде ряда
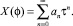
Подставляя X(φ) в уравнение (9) и приравнивая коэффициенты при одинаковых степенях τ, получим рекуррентные формулы для вычисления коэффициентов an:
a0 = 0; a1 = 1;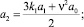 
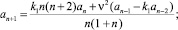
n = 1, 2, ...
Полагаем
.
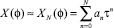Ряд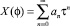 
быстро сходится при всех значениях φ, так как при n >> 1 и максимальном значении τ(0) = 1 его остаток эквивалентен ряду из членов бесконечно убывающей геометрической прогрессии со знаменателем q = k1.
Таким образом, нормированное решение уравнения (5)
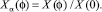
Неизвестные постоянные в (6) и (7) определяются из граничных условий и условий непрерывности и гладкости решений.
В непроницаемой части подшипника, расположенной между линией наддува и торцом подшипника, решения будем искать в виде:
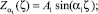
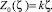
В осевом сечении с максимальным давлением (φ = 0):
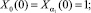
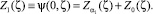
Коэффициенты A1 и α1 определятся из условия максимума давления в сечении ζ = ζ1, где ζ1 = L1/L – относительная координата линии наддува, т.е. из условий: Z1(ζ1) = 1,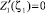 
, что эквивалентно системе уравнений
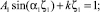
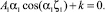
Откуда находим
,
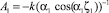где α1 – корень уравнения
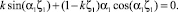
Аналогично в непроницаемой части подшипника, расположенной между линиями наддува:
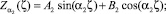
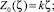
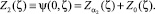
Из условий максимума давления в сечении ζ = ζ1 и отсутствия перетекания смазки в сечении ζ = 1: Z2(ζ1) = 1;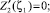 
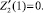
Последние равенства эквивалентны системе уравнений:
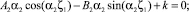
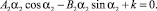
Откуда находим:
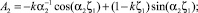
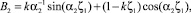
где α2 – корень уравнения
.
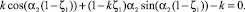Подставляя найденные решения в (8), получим:
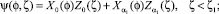
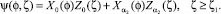
Таким образом, квадрат давления определяется по формулам:
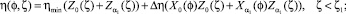
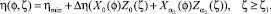
Работа подшипника в гибридном режиме вращение вала в отличие от случая работы в режиме подвеса приводит к асимметричному распределению давления газа в зазоре подшипника [4, 5, 7, 10]. Вследствие этого вал смещается от равновесного положения в направлении своего вращения и образует отличный от нуля угол ориентации нагрузки θ.
Дифференциальное уравнение для поля давления в этом случае принимает вид
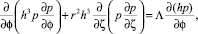(10)
где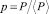 
– относительное давление; ⟨P⟩ – среднее давление в зазоре подшипника, работающего в режиме подвеса, 
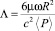– число сжимаемости.
Будем считать, что в гибридном режиме работы поле давления в зазоре подшипника формируется двумя независимыми составляющими: давления внешнего наддува газа, найденного выше, и давления pω = pω(φ), обусловленного эффектом смазочного клина. Тогда уравнение (10) для pω = pω(φ) принимает вид
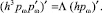
Первым интегралом этого уравнения является
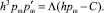(11)
Разложим относительное давление в ряд по степеням ε:
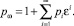(12)
Постоянная интегрирования C в уравнении (11) также зависит от ε, поэтому: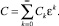 
. Подставляя эти разложения в уравнение (11), получим
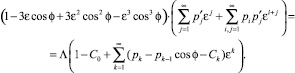(13)
Отсюда сразу находим C0 = 1. Приравнивая коэффициенты при одинаковых степенях ε, получим, что (13) – бесконечная система линейных обыкновенных дифференциальных уравнений. Решения уравнений системы (13) содержат постоянные интегрирования, которые определяются из условия [2]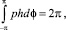 
, откуда получим
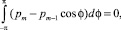m = 1, 2, .... (14)
Первое уравнение системы (13) имеет вид
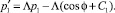
Его решение
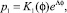
где
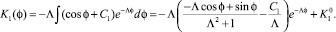
Таким образом,
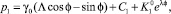
где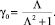 
Постоянная интегрирования 
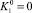из условия периодичности функции p1 (p1(–π) = p1(π)), а постоянная C0 = 0 из первого равенства системы (14) (m = 1).
Окончательно:
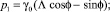
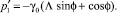
Второе уравнение системы (13) примет вид
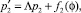
где
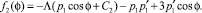
Подставляя в эти уравнения найденные p1 и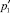 
и используя формулы тригонометрии, находим:
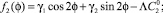
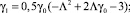
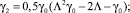
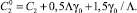
Решением второго уравнения является функция
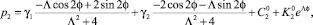
при этом из условия периодичности функции p2 получим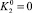 
, а из системы (13) при m = 2 находим 
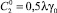. Таким образом,
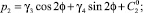
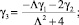
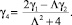
Третье уравнение системы (13)
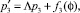
где
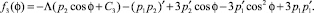
Функция f3(φ) выражается через синусы и косинусы одинарного и тройного углов:
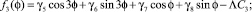
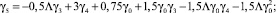
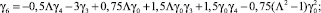
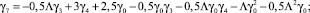
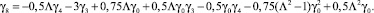
Интегрируя третье уравнение системы (13) с использованием третьего равенства системы (14), получим:
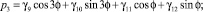
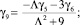
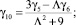
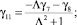
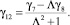
При интегрировании уравнений системы (13) коэффициенты γi прямо пропорционально зависят от малых величин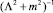 
и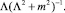 
В связи с этим при m ≥ 4 слагаемыми 
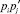можно пренебречь.
Таким образом, при m ≥ 4 уравнения имеют вид
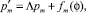
где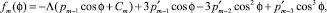 
которые легко интегрируются.
В результате получим приближенное решение уравнения (11) с точностью o(ε5):
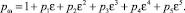
Квадрат давления находится по формулам
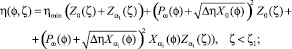
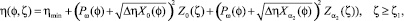
где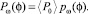 
Сравнение теоретических результатов расчета с экспериментальными данными проводилось по коэффициенту несущей способности CQ.
Зависимости коэффициента несущей способности подшипника CQ от относительного эксцентриситета ε при Kc = 0,266, r = 0,833 и ζ1 = 0,5 показаны на рис. 2.
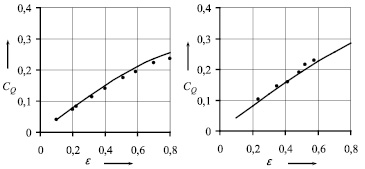
Рис. 2. Зависимости коэффициента несущей способности CQ от относительного эксцентриситета ε: а – неподвижный вал (Λ = 0; ps = 0,167), б – вращающийся вал (Λ = 0,126;ps = 0,362) – теория; • – эксперимент
Сравнение расчетных и опытных данных показывает их вполне удовлетворительную для инженерной практики точность. Относительная погрешность при определении CQ не превосходит 8 %.
Работа выполнена в рамках гранта Российского фонда фундаментальных исследований (код проекта 11-08-00049-а).
Рецензенты:
Феоктистов С.И., д.т.н., профессор, зав. кафедрой «Технология самолетостроения», ФГБОУ ВПО «Комсомольский-на-Амуре государственный технический университет», г. Комсомольск-на-Амуре;
Биленко С.В., д.т.н., доцент, зав. кафедрой «Технология машиностроения», ФГБОУ ВПО «Комсомольский-на-Амуре государственный технический университет», г. Комсомольск-на-Амуре.
Работа поступила в редакцию 18.06.2013.