Постановка задачи. Допущения. Пластическое формование керамической массы в вакуумных шнековых прессах [7] является основным технологическим процессом в производстве керамических камней, так как дефекты, приобретенные на данном этапе, не могут быть исправлены на последующих стадиях изготовления кирпичей. Адекватное управление процессом требует знания математической модели «течения» [7] керамической массы в формующем звене. При разработке математической модели исследуемого технологического процесса введен ряд упрощений и допущений.
1. Считаем, что предварительная обработка глины (до поступления в формующее звено) обеспечивает удаление из нее пузырьков воздуха, поэтому пренебрегаем сжимаемостью керамической массы.
2. Принимаем, что для производства керамических камней используется однородное сырье, поэтому плотность глинистых частиц остается неизменной по всему объему пресса и формующего звена.
3. Допускаем, что применяемый для увлажнения пар и/или вода имеют постоянную температуру, а поэтому формование керамических камней в прессе представляет собой изотермический процесс.
Математическая модель «течения» керамической массы в формующем звене
Вводимые в рассмотрение упрощения и допущения позволяют рассматривать формование керамических камней в формующем звене, выполненном в виде воронки с прямоугольным выходным сечением, как изотермический процесс «течения» неньютоновской жидкости [7] с неизменными физико-химическими свойствами под действием усилия, создаваемого шнеком. Поэтому для описания технологического процесса формования как объекта управления (в котором в качестве выходной координаты принимаем на основании работы [1] скорость сдвиговых деформаций в рабочем объеме формующеего звена, управляющими воздействиями являются угловая скорость шнека и влажность сырца, основное возмущение – изменение физико-химических свойств керамической массы) используем систему дифференциальных уравнений Навье‒Стокса, которая описывает динамику вязкой несжимаемой жидкости в изотермических условиях, и уравнение неразрывности потока керамической массы:
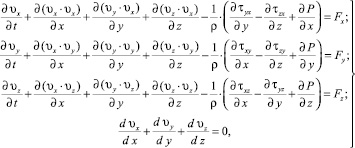(1)
где υx, υy, υz – проекции вектора скорости на оси x, y, z; τxy = τyx, τyz = τzy, τzx = τxz – касательные напряжения; Р – давление керамической массы в рассматриваемой точке; ρ – плотность керамической массы; Fx, Fy, Fz – проекции внешней силы, отнесенной к единице массы; t – время.
Тензор вязких сдвиговых напряжений [2, 6, 7, 10]:
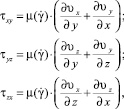
где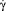 
– скорость сдвиговых деформаций,
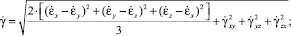
здесь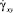 
, 
, 
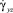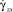– компоненты этой скорости,
, 
, 
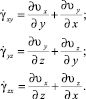
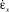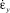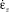– скорости линейных деформаций, с учетом несжимаемости керамической массы
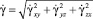
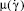– эффективная вязкость, 
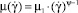, здесь μ1 – коэффициент консистенции, μ1 = f(w) , w и ψ – влажность и индекс течения керамической массы.
Система дифференциальных уравнений (1) дополнена граничными и начальными условиями. Граничные условия (ГУ) формующего звена сформулированы на основании общепринятых допущений, характерных для описания процесса движения керамической массы и практики эксплуатации вакуумных шнековых прессов:
ГУ1 – скорости частиц формуемой массы на стенках
υст = 0; (2)
ГУ2 – функция распределения скоростей керамической массы на входном торце получена по результатам моделирования скоростей течения неньютоновской жидкости через кольцевое сечение (которым представляется пространство, образованное корпусом пресса и ступицей шнекового вала), выполненное с использованием материалов, представленных в работах [3, 5]:
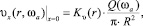(3)
где r – текущее значения радиуса входного цилиндра воронки, r ∈ 0, ..., R, R – радиус цилиндра, ωа – угловая скорость шнека, Q(ωа) – расход керамической массы; Kυ(r) – коэффициент, зависящий от текущего значения радиуса;
ГУ3 – давление керамической массы на выходном торце (при x = L, L – длина формующего звена)
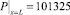Па (4)
принято на основании результатов исследований [9, 11] шнекового пресса.
Под начальными условиями понимается режим работы пресса, когда формующее звено заполнено керамической массой, а скорость шнека ωa = 0. В этом случае:
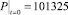Па, (5)
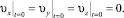(6)
Пример моделирования поля скоростей сдвиговых деформаций. На примере шнекового вакуум-пресса Händle PZG 60b/50 [6], оборудованного формующим звеном для выпуска полнотелых кирпичей 250×120×65 ГОСТ 530-2007, в программной среде Solid Works на основании уравнений (1) с учетом краевых условий (2)–(6) создана вычислительная модель поля скоростей сдвиговых деформаций керамической массы в формующем звене.
Модель представляет собой состояние многомерного технологического объекта с распределенными параметрами. Здесь в качестве выходной координаты выбрана скорость сдвиговых деформаций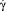 
в рабочем объеме формующего звена и линейная скорость υx на выходном торце. Величина 
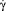определяется двумя управляющими воздействиями – угловой скоростью шнека ωa и влажностью w. Основным возмущением является индекс течения ψ.
Методика постановки вычислительных экспериментов заключалась в оценке характеристик поля скоростей сдвиговых деформаций в квазистатическом режиме при постоянных дискретных значениях влажности wi керамической массы, которым соответствует коэффициент консистенции
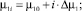i = 0, 1, ..., 4;
μ10 = 10000 Па·с; Δμ1 = 30000 Па·с;
дискретных постоянных значениях индекса течения керамической массы
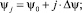j = 0 , 1, 2;
ψ0 = 0,1; Δψ = 0,1
и скачкообразном изменении скорости шнека
,
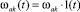где
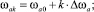k = 0, 1, ..., 5;
ωa0 = 0,5 рад/с; Δωa = 0,5 рад/с.
Материалы расчета на вычислительной модели содержат в себе и переходную составляющую, и установившийся режим. В данной статье приводятся результаты исследования установившегося режима.
Из анализа материалов моделирования можно сделать следующие выводы:
1. Результаты расчета координаты υx были использованы для их сравнения с экспериментальными значениями скорости движения керамической массы на выходе формующего звена, полученными в работе [4]. Сравнение распределения скорости υx на выходном торце формующего звена, полученного на модели (кривая 1, рис. 1), с экспериментально полученным в [4] распределением скорости на подобном прессе (кривая 2) показало, что отклонение не превышает 5 %. Здесь по оси абсцисс отложено относительное значение ширины выходного сечения, по оси ординат ‒ относительное значение скорости, за базовое значение скорости принята ее максимальная величина. Поэтому считаем, что разработанная математическая модель адекватно описывает исследуемый технологический процесс как объект управления.
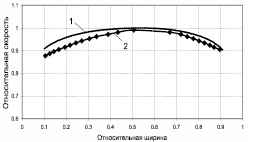
Рис. 1. Оценка адекватности модели:1 – скорость υx на выходном торце формующего звена, полученная на модели; 2 – экспериментально полученная скорость υx
2. Поле скоростей сдвиговых деформаций керамической массы в формующем звене вакуумного шнекового пресса в исследуемом диапазоне изменения влажности практически не зависит от w, но существенно зависит от индекса течения ψ (рис. 2).
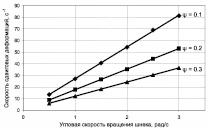
Рис. 2. Зависимость скорости сдвиговых деформаций от частоты вращения шнека (при различных индексах течения керамической массы)
3. Анализ поля распределения скорости сдвиговых деформаций по объему формующего звена показал, что максимальная ее величина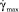 
наблюдается на горизонтальных стенках выходного сечения.
4. Установлена линейная зависимость (рис. 2) максимальной скорости сдвиговых деформаций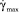 
от скорости вращения ωa шнека.
Рецензенты:
Лысов В.Е., д.т.н., профессор кафедры «Электропривод и промышленная автоматика» Самарского государственного технического университета, г. Самара;
Данилушкин А.И., д.т.н., профессор кафедры «Электроснабжение промышленных предприятий» Самарского государственного технического университета, г. Самара.
Работа поступила в редакцию 17.05.2013.