Обзор работ, касающихся вопросов уплотнения, консолидации и разрушения некомпактных и пористых материалов, приведен в работе [4]. Прикладная теория пластичности пористых тел изложена в работе [1]. Показано, что в процессе пластического деформирования некомпактные и пористые материалы испытывают значительную необратимую деформацию изменения объёма, что принципиально отличает их от несжимаемых тел. При этом для моделирования процессов уплотнения таких материалов используют два основных подхода: феноменологический [1, 5] и структурно-феноменологический [2, 3]. Феноменологический подход не позволяет учесть влияние формы пор, геометрических параметров пор и их распределение по объему на процессы пластического формоизменения деформируемых пористых тел. Для структурно-феноменологического подхода характерно использование связи геометрической структуры пористого тела и физико-механических свойств зернистого каркаса со свойствами сопротивления сжимаемых сред необратимому формоизменению. При этом используются континуальные представления о деформируемой среде, реологические характеристики которой получают в результате анализа элементов структуры. В настоящее время существует значительный ряд работ, в которых рассмотрены и обобщены основные положения, используемые при решении задач механики структурно-неоднородных материалов, построены замкнутые системы уравнений движения гетерогенных смесей при заданных физико-химических свойствах структурных составляющих. Однако проблема количественного описания многообразия процессов деформирования рассматриваемых сред не может считаться окончательно решенной.
Целью работы является решение задач технологической механики для совершенствования процессов уплотнения некомпактных и пористых материалов с использованием методов компьютерного моделирования; теоретическое обобщение исследований процессов формования металлических заготовок из порошкообразного сырья и создание научно-обоснованных предпосылок для разработки новых технологических процессов прессования и выдавливания высокоплотных заготовок.
Для решения поставленных задач приняли допущение, что уже незначительное приращение сжимающей нагрузки вызывает уменьшение объема уплотняемого материала. Это дает основание считать, что упругая деформация такого материала несущественно влияет на его уплотнение. Скорости пластической деформации пропорциональны напряжениям в текущий момент; напряженное состояние определяет мгновенные приращения компонент пластической деформации. Для определения приращений пластической деформации dεij используется функция Φ(σij), называемая пластическим потенциалом. Вид этой функции задается таким образом, чтобы уравнения пластического течения можно было представить в виде
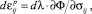
где dλ ≥ 0 – некоторый неопределенный малый скалярный множитель. Для теории пластичности важен случай, когда функция пластичности и пластический потенциал совпадают, т.е. f = Φ. При этом относительно легко устанавливаются принципы экстремальности и теорема единственности, что сообщает теории законченность. В этом случае выполняется ассоциированный закон пластического течения.
Для изотропных пластически деформируемых сжимаемых материалов имеем
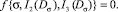(1)
Тогда в соответствии с ассоциированным законом пластического течения
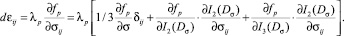(2)
В современных расчетных комплексах, основанных на методе конечных элементов, для моделирования процессов пластического деформирования некомпактных (пористых) материалов используют модели Cam-Clay Plasticity, Porous metal plasticity и др. Одной из таких моделей является так называемая модифицированная модель текучести Друкера‒Прагера (Modified Drucker-Prager cap), также известная как DPC-модель [6]. На рис. 1 приведена трехмерная интерпретация DPC-модели.
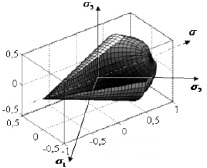
Рис. 1. Вид замкнутой поверхности текучести Друкера‒Прагера (3/4 модели) σ1, σ2, σ3, σ – главные напряжения и гидростатическое давление, представленные в безразмерном виде
Для DPC-модели предельная поверхность в плоскости σ–τ (первого и второго инвариантов тензора напряжений соответственно) представляет собой прямую, а поверхность текучести – дугу эллипса. Протяженность вдоль гидростатической оси со стороны отрицательных значений среднего напряжения определяется пределом текучести на всестороннее сжатие. В отличие от эллиптического на коническом участке действует неассоциированный закон течения. Вектор скоростей деформаций ортогонален только к эллиптической поверхности, а его направление в случае, когда поверхность нагружения совпадает с поверхностью текучести, зависит от значения среднего нормального напряжения. Обычно принимают, что коническая составляющая поверхности в процессе деформации остается неизменной эволюции подвергается только эллиптический участок.
Для определения предельной поверхности DPC-модели достаточно провести испытания на радиальное и осевое сжатие цилиндрических образцов. Для определения эллиптического участка необходимо реализовать гидростатическое сжатие и прессование в закрытой пресс-форме. Так как для испытаний на гиростатическое сжатие высокопрочных металлических порошков, например, сплава титана ВТ-22 требуется сложное и дорогостоящее оборудование, возникает необходимость заменить натурные испытания имитационным моделированием. Чтобы сравнить результаты экспериментальных исследований с результатами имитационного моделирования в качестве модельного материала выбрали хорошо изученные порошки меди.
Во многих случаях при исследовании процессов деформирования структурно-неоднородных материалов могут быть использованы модели микронеоднородных сред с регулярной структурой, в которой можно выделить представительные элементы – ячейки. На рис. 2 показана объемная модель представительной ячейки деформируемого материала. Для осуществления имитационного моделирования (рис. 3) процессов гидростатического сжатия, компактирования в закрытой пресс-форме, а также сдвига ячейки представительного объёма уплотняемого тела применили пакет конечно-элементного анализа ABAQUS (студенческая версия). На рис. 4 приведена зависимость пластических модулей psи τs при гидростатическом сжатии и чистом сдвиге от относительной пористости.
Рис. 2. Модель представительной ячейки пористой меди
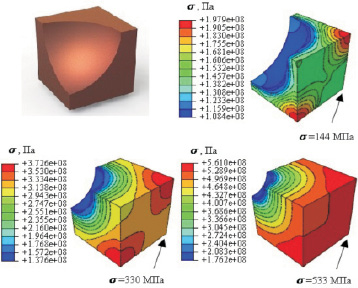
а
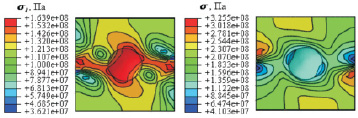
б в
Рис. 3. Результаты имитационного моделирования процессов гидростатического сжатия (а) и сдвига (б, в) ячейки представительного объёма пористого тела:а – поле среднего нормального напряжения (гидростатическое сжатие); б – поле интенсивности напряжений (сдвиг); в – поле среднего нормального напряжения (сдвиг)
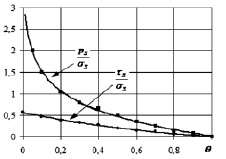
Рис. 4. Зависимость пластических модулей ps и τs при гидростатическом сжатии и сдвиге ячейки представительного объёма от пористости (σs – предел текучести меди при нулевой пористости)
Результаты исследования процессов уплотнения некомпактного материала из меди при гидростатическом сжатии и сдвиге на 3D-моделях показали хорошую сходимость расчётных и экспериментальных данных, приведенных в работах [1, 4, 5], что позволило использовать имитационное моделирование для идентификации определяющих уравнений и решения задач пластической деформации сжимаемых сред на основе порошков из высокопрочного сплава титана ВТ-22.
Выполненные исследования позволили разработать имитационные модели достаточно сложных задач технологической механики пористых тел: полунепрерывное выдавливание заготовки и формование детали сложной формы из металлического порошкообразного сырья.
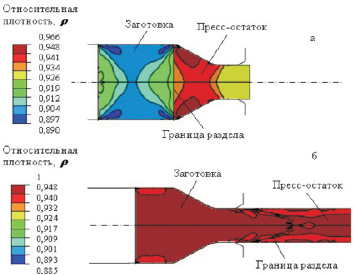
Рис. 5. Распределение относительной плотности ρ по сечению выдавливаемой заготовки:а – распрессовка заготовки; б – выход границы раздела заготовок из калибрующего пояска матрицы
На рис. 5 показано распределение относительной плотности по сечению заготовки для случая начальной пористости ρз = 0,89 при угле матрицы 2α = 60° и вытяжке μ = 4,94 на различных стадиях процесса выдавливания. Видно (рис. 5, а), что относительная плотность материала брикета, деформированного в непосредственной близости от пуансона, приближается к плотности пресс-остатка. Далее материал брикета проходит через коническую часть матрицы с малым изменением плотности, что объясняется недостаточным уровнем средних нормальных напряжений, отвечающих за изменение объема. При этом наибольшая скорость истечения материала находится на оси симметрии заготовки (рис. 5, б). На выходе из калибрующего пояска матрицы вид напряженного состояния меняется: продольная компонента тензора напряжений переходит от сжатия к растяжению, вследствие чего наблюдается незначительное разуплотнение. Следует отметить, что в принятом диапазоне значений μ и α относительная плотность материала ρ на выходе из очага деформации несущественно зависит от начальной пористости заготовки ρз.
Результаты вычислительного эксперимента были обработаны с помощью регрессионного анализа в программном комплексе компьютерной математики MATLAB. Это позволило установить зависимости параметров процесса выдавливания, таких как пористость θ и давление выдавливания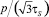 
от угла α и вытяжки μ:
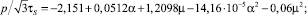(3)
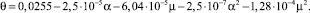(4)
Результаты натурного эксперимента показали пригодность разработанной имитационной модели для совершенствования технологии полунепрерывного выдавливания заготовок из порошкообразного металлического сырья.
Заключение
Разработан экспериментально-аналитический метод нахождения внутренних переменных в определяющих соотношениях уплотняемой среды. С этой целью строится объемная модель представительной ячейки и осуществляется имитационное моделирование процесса пластического течения пористой массы. Предложены простые методы для определения пределов текучести на всестороннее сжатие и сдвиг уплотняемых материалов. Осуществлено компьютерное моделирование процесса полунепрерывного выдавливания пористой заготовки, позволившее установить зависимости усилия выдавливания и пористости выдавленных заготовок от основных параметров процесса.
Рецензенты:
Поляков А.П., д.т.н., доцент, ведущий научный сотрудник лаборатории системного моделирования Института машиноведения УрО РАН, г. Екатеринбург;
Лехов О.С., д.т.н., профессор, заведующий кафедрой механики машиностроительного факультета, РГППУ, г. Екатеринбург.
Работа поступила в редакцию 18.06.2013