Описание предметной области
Решающим этапом в торгово-хозяйственной деятельности многих организаций является процесс производства и сбыта продукции. Важнейшая проблема этого этапа ‒ приведение темпа производства и темпов продаж продукции в соответствие с требованиями конечного потребителя-заказчика. Как показывает практический опыт, темпы производства часто изменяются в больших интервалах, чем фактические темпы потребительских покупок. Известно, что сбытовая система с цепью взаимосвязанных товарных запасов и определенным порядком выдачи заказов на их пополнение имеет тенденцию усиливать небольшие изменения, возникающие в розничной торговле. Мы излагаем структуру и образ действий многоуровневой сбытовой системы [1].
На рис. 1 показана организационная структура для производства и сбыта продукции. В рисунке объектом производства могут быть любые организации, производящие товаров по заказам потребителей. Далее готовая продукция хранится на складе. Продажа готовой продукции осуществляется в оптовой и розничной торговле с учетом заказов потребителей.
Процесс выполнения заказа потребителей можно рассматривать как иерархический (рис. 1).
Для поддержания высокой производительности торгово-хозяйственной деятельности предприятий необходимо контролировать и регулировать значения управляющих параметров. Для этого требуется предварительно разработать математическую модель процесса выполнения заказов, оценить ее параметры по экспериментальным данным, а также найти оптимальные значения управляющих параметров.
Математическая модель процесса выполнения заказов потребителей
Сначала рассмотрим различные модели выполнения заказов потребителей и далее показываем задачу идентификации в обобщенном виде.
1. Моделирование заказов потребителей с помощью логистической функции. Заказ на многие товары с течением времени возрастает: сначала медленно, затем быстро и, наконец, снова замедляется за счет насыщения. Это значит, что скорость увеличения заказа прямо пропорциональна обеспеченности и насыщению товаром. Для построения модели введем обозначения:
t – время;
y – обеспеченность товаром;
A – насыщенность товаров;
k – коэффициент пропорциональности.
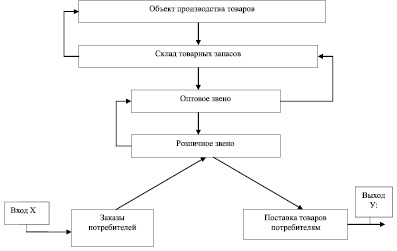
Рис. 1
Тогда зависимость обеспеченности от времени выражается дифференциальным уравнением
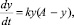
и получаем решение этого уравнения в виде логистической функции
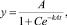
где параметры A и k определяются по методу наименьших квадратов. Для нахождения постоянной C можно потребовать, чтобы функция проходила через последнюю точку, то есть выполнялось условие
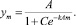
Решая последнее уравнение относительно C, получаем
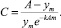
Окончательно получим формулу зависимости заказа от времени
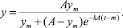
Прогноз заказов получают при подстановке в эту формулу значений t > m.
2. Моделирование заказов с помощью логарифмически нормального закона. В основе такой модели используется гипотеза о том, что обеспеченность товаром подчиняется интегральному логарифмически нормальному закону
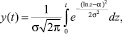
где y(t) – обеспеченность товаром к моменту времени t; α, σ – неопределенные параметры функции.
Очевидно, для этой гипотезы при всех t должны выполняться неравенства 0 ≤ y(t) ≤ 1. Чтобы пользоваться формулой интегрального логарифмически нормального закона, надо определить параметры α и σ. С этой целью делают замену переменных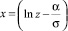 
, тогда получают
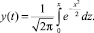
В этой формуле выражение справа является интегралом Гаусса, для которого составлены таблицы значений.
Для определения α и σ применяют формулу
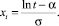
Зная значения y(t) за прошлые годы t = 1, 2, ..., m, из таблиц для интеграла Гаусса находят xt (t = 1, 2, ..., m). Обозначив,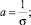 
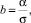получают xt = aln t – b.
Применяя метод наименьших квадратов, находят a и b, при которых
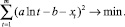
Затем находят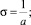 
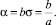
Тогда получают известную функцию, с помощью которой можно определить прогноз обеспеченности y(t) если t > m.
Можно также решать задачу определения номера года t1, в котором обеспеченность достигает заранее заданного значения. Для этого считается известным y(t1) = y1, затем по таблицам для интеграла Гаусса находят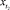 
и, наконец, находят t1, 
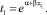Этот метод можно использовать и в том случае, когда обеспеченность y(t) > 1, но для этого надо знать предельное значение обеспеченности и в качестве y(t) рассматривать y(t)/A.
3. Определение заказов на основе анкетных опросов. Этот метод использует анкеты, содержащие сведения о желаемой очередности покупок определенного набора товаров, а также данные о реальной очередности покупок этих товаров в прошлом. На основании этих данных определяют вероятности Pij того, что i – товар будет куплен j-м по очередности, т.е. получают квадратную матрицу вероятностей P = (Pij). Затем определяют удельный вес покупателей si, имеющих в наличии i видов товаров (i = 1, 2, ..., n – 1). Назовем емкостью рынка набор вероятностей ri того, что покупатель, приобретая какой-либо товар, купим именно i-е товар. Обозначим
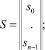
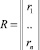
Тогда емкость рынка R = PS. Зная емкость рынка R, можно определить заказ на товары.
Рассмотрим следующий пример. Пусть на основе анкет определена матрица вероятностей очередностей покупок трех видов товаров: 1 – стиральные машины, 2 – холодильники, 3 – пылососы. Кроме того, имеются данные об удельном весе этих товаров, имеющихся у покупателей
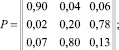
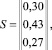
тогда емкость рынка будет
Итак, вероятность покупки стиральной машины равна 0,3; холодильника – 0,3; пылесоса – 0,4 при условии, что покупка будет совершена. Пусть известно, число покупателей на рынке равна Q. Если считать, что покупатель обязательно купит хотя бы один из этих товаров, то спрос составит: на стиральные машины 0,3Q, на холодильники 0,3Q, на пылесосы 0,4Q.
Надо отметить, что для прогнозирования заказов на товары длительного пользования используют и другие методы прогнозирования, среди которых особенно следует отметить методы, основанные на определении зависимостей заказа от величины факторов, влияющих на образование заказов. Основные положения этих методов состоят в определении главных факторов, влияющих на заказ, значений этих факторов, на прогнозируемый период и функции, выражающей зависимость заказа от главных факторов. Для выбора функции, выражающей зависимость заказа от факторов, можно применять многофакторные модели [5].
Определение научно обоснованного заказа на продукцию и особенно на товары народного потребления является сложной и очень важной задачей. Использование математических моделей и методов помогает решать эти задачей. Наиболее подходящими являются многофакторные модели. При использовании таких моделей необходимо, чтобы специалисты торговых предприятий очень тщательно отобрали основные факторы, влияющие на заказ, и получили значения этих факторов в прогнозируемом периоде. Это также является сложной задачей, но от ее решения зависит успех применения моделей. Следует отметить также, что имеются и другие подходы, методы и способы для определения заказа. Однако они имеют свои недостатки. Поэтому целесообразно выбирать метод прогнозирования с учетом специфических особенностей торговых предприятий и прогнозируемых показателей.
Идентификация математической модели обеспеченности товарами
Для практического использования вышеизложенных моделей необходимо решить задачу идентификации параметров системы обыкновенных дифференциальных уравнений (ОДУ) по временному ряду статистических данных [2, 3].
Пусть имеется система ОДУ
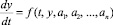(1)
с начальными условиями
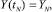
где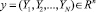 
– вектор фазовых переменных модели, объём товара i-го предприятия (i = N, ..., 1);
– вектор коэффициентов, неизвестные, которые принадлежат к идентификации;
f(t, y, a) ‒ вектор функции, с размерностью (n×m), описывающей закономерности развития торгового объекта и имеющая первые и вторые производные правой части по y.
Для идентификации вектора коэффициентов задачу (1) запишем в виде конечноразностных схем:
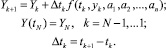(2)
Для определения коэффициентов a1, a2, ..., an к уравнению (2) применим метод наименьших квадратов:
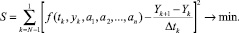(3)
Отсюда, получаем систему нормальных уравнений:
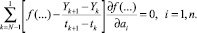(4)
Определив постоянные коэффициенты {ai, i = 1,n}, решив систему (4), произведем вычисления в режиме «адекватность-прогноз». Проверка адекватности модели осуществляется вычислением значении функции в точке:
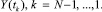
Прогнозные значения функции вычисляются в точке
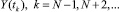
Для получения теоретических значений y(t) для системы (1) решается задача Коши с начальным условием Y(tN) = YN. Численное решение системы (1) осуществлялось методом Рунге‒Кутты 4-го порядка, обладающим хорошими показателями скорости сходимости при сравнительно низких вычислительных затратах. В качестве алгоритма минимизации целевой функции (3) выбран алгоритм с вещественным кодированием [4]. Этот алгоритм эффективно решает многоэкстремальные задачи и задачи высокой размерности. Программным обеспечением данной задачи являлись офисные программы Windows XP и пакет прикладных программ Maple [6].
Оценкой качества математической модели является корень из среднеквадратического отклонения теоретических и статистических значений:
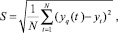
где yq(t)теоретическое значение показателя в t – момент, вычисленный по q-й функции на базе всех N – точек; yt – статистические данные по t-му году.
Результаты идентификации математической модели
Идентификация математической модели осуществлялась на примере заказа потребителей на пищевые продукты. В данном примере указана тенденция заказа на рисовые культуры. В качестве входных данных рассматривались ежегодные статистические данные по рису (табл. 1).
Таблица 1
|
Годы |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
|
Число (y) заказов на рис, тыс. тонн |
10 10 |
13 |
17 |
16 |
26 |
23 |
29 |
36 |
41 |
46 |
44 |
48 |
Значения параметров, используемых для идентификации модели, вычислены на основе анализа статистических данных для рассматриваемых видов сырья.
Пусть скорость обеспеченности заказа потребителей на рисовые продукты имеет линейный закон развития социально-экономических процессов предприятия торговли
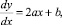
где a и b ‒ неизвестные параметры, которые необходимо определить по статистическим данным.
Используя вышеизложенные методики вычисления, по формулам (1)–(4) находим: a = 1,8549; b = 4,9696. Тогда конкретный вид модели имеет:
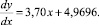
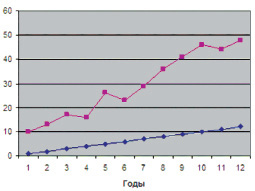
Рис. 2. Число заказов на рис (тыс. т)
Результаты моделирования на базовом периоде приведены на табл. 2, и графическая интерпретация динамики спроса на рис показана на рис. 2.
Таблица 2
|
Xi |
Число (y) заказов на рис тыс. тонн |
||
|
Модель |
Стат. |
Разница |
|
|
12 11 10 9 8 7 6 5 4 3 2 1 |
49,3696 44,7 41,9696 38,2696 34,5696 30,8696 27,1696 23,4696 19,7696 16,0696 12,3696 8,0696 |
48 44 46 41 36 29 23 26 16 17 13 10 |
1,3696 0,7 -4,0304 -2,7304 -1,4304 1,8696 4,1696 -2,5304 3,7696 -0,9304 -0,6304 -1,9304 |
Анализ представленных результатов показывает, что исследуемая математическая модель достаточно хорошо описывает эмпирические зависимости для периода 2001–2012 годы.
Выводы по работе
Предложена математическая модель, описывающая процесс выполнения заказов потребителей для получения товарной продукции. Проведена идентификация параметров данной модели на примере заказов потребителей на рисовую продукцию. В работе приведено сопоставление экспериментальных и расчетных данных. Их удовлетворительное соответствие показывает возможность применения предложенной модели для прогнозных расчетов. Теоретическое исследование процесса торговли, создание математических моделей позволяет, с одной стороны, производству получить максимальную прибыль, с другой стороны, выгодно и потребителю товаров. Организация процесса торговли в условиях новых хозяйственных форм и исследование поддержки принятия решений для самоорганизации социально-экономических систем предприятия торговли позволяет оптимально управлять выполнением заказов потребителей различных слоев общества.
Рецензенты:
Зольников В.К., д.т.н., профессор, заведующий кафедрой «Вычислительная техника и информационные системы», ВГЛТА,г. Воронеж;
Межов В.Е., д.т.н., профессор кафедры «Вычислительная техника и информационные системы», ВГЛТА, г. Воронеж.
Работа поступила в редакцию 07.06.2013