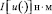Задачи оптимального управления динамическими объектами являются важными и актуальными. Дифференциальные уравнения движения для таких объектов, как правило, бывают нелинейными, что затрудняет применение известных методов оптимизации, например, принципа максимума Л.С. Понтрягина. В статье рассматривается задача о возвращении схвата двухзвенного манипулятора на базовую траекторию. Для ее решения уравнения движения схвата были линеаризированы в окрестности этой траектории, что позволило свести задачу управления к функциональной проблеме моментов и решить ее. Кроме того, удалось расширить задачу управления до игровой и построить наилучшую гарантирующую позиционную стратегию игрока – союзника, позволяющую преодолеть самые неблагоприятные действия неконтролируемой помехи. Управления, полученные в линеаризированной модели, были применены и для исходной модели. Численный эксперимент показал приемлемость такого подхода.
1. Математическая модель манипулятор
На горизонтальной плоскости рассмотрим двухзвенный механический манипулятор с двумя вращательными парами (рис. 1). Каждое звено манипулятора представляет собой абсолютно жесткий однородный стержень длины l. Первое звено соединено с неподвижным основанием вращательной парой O1, а со вторым звеном – вращательной парой O2. Принимается, что масса схвата равна m, а масса i-го звена – mi, i = 1, 2. В соединительных парах могут развиваться управляющие моменты wi, i = 1, 2. Трение в шарнирах отсутствует. В статьях [1], [5] были выведены дифференциальные уравнения движения данного манипулятора в форме уравнений Лагранжа второго рода, в которых в качестве обобщенных координат взяты углы φi, i = 1, 2. Вид этих уравнений приводится ниже
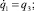
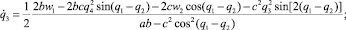(1.1)
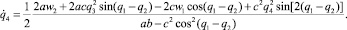
Здесь
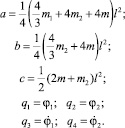
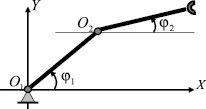
Рис. 1. Двухзвенный манипулятор
Связь между декартовыми координатами схвата и обобщенными координатами манипулятора осуществляется по формулам
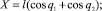
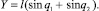(1.2)
Заданы: t0 = 0начальный и T – конечный моменты времени процесса, (X0, Y0)исходное и (XT, YT) конечное положение схвата, Y = f(X) уравнение траектории схвата,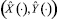 
– базовый закон изменения декартовых координат схвата в функции времени, обеспечивающий его переход из начального положения в конечное вдоль траектории Y = f(X) с нулевыми начальной и конечной скоростями. Для определения программных управлений 
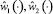, реализующих базовый закон движения схвата, следует обратить соотношения (1.2) и, подставив в полученные зависимости закон движения 
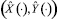, найти соответствующий ему закон изменения обобщенных координат 
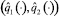. Управления 
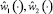легко определяются из соотношений (1.1), если положить в них
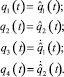
Таким образом, управления также считаем заданными.
2. Постановка задачи управления.
Пусть по какой-либо причине в начальный момент времени схват не находится строго на заданной траектории. Тогда управления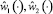 
не обеспечат для него базовый закон движения 
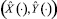и, в частности, движение вдоль траектории Y = f(X) с остановкой в конечный момент времени T. Допустим, что в каждой из вращательных пар могут развиваться дополнительные управляющие моменты u1, u2 соответственно. Тогда дифференциальные уравнения движения манипулятора запишутся в виде
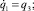
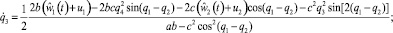(2.1)
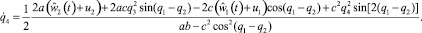
Требуется подобрать моменты u1, u2 в виде интегрируемых функций времени, возвращающие схват на заданный закон движения в момент времени ϑ ∈ [t0, T] и доставляющие минимум критерию качества
.
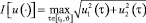По терминологии книги [2], этот критерий носит название «минимум силы».
Сформулируем проблему как задачу теории оптимального управления. Пусть (X0, Y0) – начальное положение схвата, не принадлежащее заданной траектории, (q10, q20) – отвечающие ему обобщенные координаты, и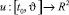 
– некоторая интегрируемая вектор-функция. Символом 
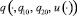обозначим соответствующее решение системы дифференциальных уравнений (2.1) с начальными условиями
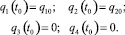
Задача 1. Среди интегрируемых вектор функций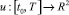 
, удовлетворяющих условию
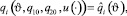i = 1, ..., 4,
найти ту, для которой величина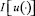 
достигает наименьшего значения.
Усложним модель. Предположим, что в соединительных парах могут развиваться неконтролируемые помехи в виде вращательных моментов v1, v2. Неконтролируемой помехе предписывается стремление максимально навредить в решении задачи перевода схвата на базовую траекторию. В данной модели конфликтно-управляемого динамического объекта на дополнительные управления u1, u2 и неконтролируемые помехи v1, v2 наложены геометрические ограничения в форме включений
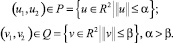
Рассматриваемую ситуацию будем трактовать как антагонистическую дифференциальную игру двух лиц, динамика которой описывается дифференциальными уравнениями
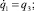
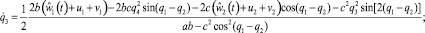
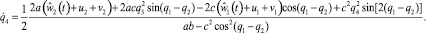
В этой игре «игрок-союзник» осуществляет управление объектом в классе позиционных стратегий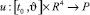 
, опираясь на информацию только о реализовавшемся в данный момент времени фазовом векторе игры. «Игрок – противник» может применять любые интегрируемые реализации вектора своих управляющих параметров 
.
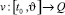3. Линеаризованные уравнения движения
Полагаем
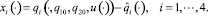(3.1)
Тогда условие возвращения схвата на базовый закон движения в момент времени ϑ принимает вид xi(ϑ) = 0, i = 1, ..., 4. Изменение во времени величин (3.1) в условиях задачи 1 приближенно описывается линейным векторным дифференциальным уравнением
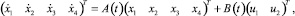(3.2)
а в условиях дифференциальной игры – уравнением
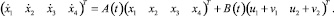(3.3)
Здесь
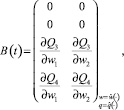
Q3, Q4 – правые части третьего и четвертого дифференциального уравнения в (1.1) соответственно. Аппроксимируем задачу 1.
Задача 2. Среди интегрируемых вектор функций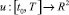 
, удовлетворяющих условию
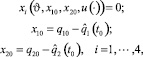
где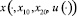 
– соответствующее решение системы (3.2) с начальными условиями (x10, x20, 0, 0), найти ту, для которой величина 
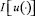достигает наименьшего значения.
Аналогично исходную дифференциальную игру аппроксимируем линейной антагонистической дифференциальной игрой двух лиц, динамика которой описывается уравнением (3.3), цель первого игрока-союзника – привести фазовый вектор игры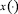 
в начало координат в момент времени ϑ, а второго игрока – максимально этому противодействовать.
4. Решение задачи 2
Решение задачи 2 осуществим методом сведения ее к функциональной проблеме моментов [2]. Пусть X[t, τ], t, τ ∈ [t0, ϑ] фундаментальная матрица Коши для однородного уравнения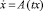 
. Полагаем H[ϑ, τ] = X[ϑ, τ]B(τ), τ ∈ [t0, ϑ], c = –X[ϑ, t0]x0, 
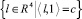. Символом 
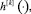k = 1, ..., 4 обозначим k-ю строку матрицы H[ϑ, τ]. Оптимальное управление 
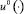, решающее задачу 2, вычисляется по формуле [2]
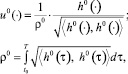
где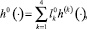 
, а вектор l0 – решение задачи математического программирования
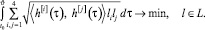
5. Решение дифференциальной игры
Аппроксимирующая дифференциальная игра является линейной дифференциальной игрой «наведения-уклонения в момент времени ϑ на целевое множество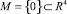 
», в которой выполнены условия однотипности. Тогда в этой игре существует [3] седловая точка в классе позиционных стратегий. Приведем основные моменты ее построения. Полагаем
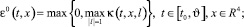(5.1)
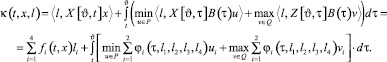
Обозначим через l0(t, x) вектор, на котором достигается максимум в (5.1). В силу однотипности объектов он единственен, если ε0(t, x) > 0. Пара позиционных стратегий ue, ve, реализующих седловую точку в игре, определяется формулами
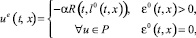
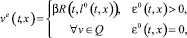(5.2)
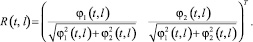(5.3)
Позиционные управления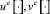 
не являются непрерывными, поэтому игру следует формализовать в классе конструктивных движений Н.Н. Красовского (пошаговые равномерные пределы ломаных Эйлера) [3], [4]. Позиционное управление 
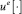«игрока-союзника» обеспечивает выход схвата манипулятора на базовый закон движения в момент времени ϑ при любых действиях помехи, если ε0(t0, x0) = 0. Опишем процедуру управления нелинейным объектом (2.2) на базе оптимальных стратегий, решающих аппроксимирующую линейную дифференциальную игру. Промежуток времени [t0, ϑ] разбиваем на полуинтервалы
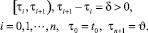
На каждом из полуинтервалов оптимальные управления игроков определяются из условия
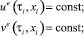
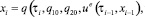
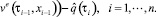
Результат управления зависит от величины δ > 0. Чем она меньше, тем ближе к теоретическому значению будет величина платы в игре.
6. Численный эксперимент
Зададимся следующими массово-геометрическими характеристиками манипулятора: m = m1 = m2 = 1 кг, l1 = l2 = 1 м. Принимаем, что t0 = 0, T = 1 с. При решении задачи 1 полагаем
(X0, Y0) = (1,5 м; 1,02 м), (XT, YT) = (0,25 м; 1,24 м),
.
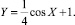Тогда
x1(0) = 10,21∙10–2 рад, x2(0) = 5,31∙10–2 рад, x3(0) = 0 рад/с; x4(0) = 0 рад/с.
Задача вывода схвата на исходную траекторию была решена для десяти значений момента времени ϑ ∈ [0,1; 1]. Оптимальное значение критерия «минимум силы» для каждого из этих моментов времени приведено в таблице.
Зависимость величины критерия от длины промежутка времени управления
|
ϑ, с |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
|
96,82 |
23,71 |
10,19 |
5,49 |
3,35 |
2,22 |
1,56 |
1,15 |
0,87 |
0,67 |
Из таблицы следует, что чем меньше времени дается на выход движения схвата на базовую траекторию, тем больше силовые затраты на управление. Эффективность найденного дополнительного программного управления проверяется путем подстановки его в исходные нелинейные дифференциальные уравнения движения и интегрирования их с выбранными смещенными начальными условиями. Численно показано, что в результате схват в момент времени ϑ выходит на базовую траекторию и продолжает движение вдоль нее после выключения дополнительных управлений. На рис. 2 приводится траектория движения схвата манипулятора для случая ϑ = 0,5.
В случае игровой задачи принимается, что
a = 10, β = 1, ϑ = 0,5, (X0, Y0) = (1,5 м; 0,38 м) (XT, YT) = (0,5 м; 1,38 м),
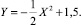
Тогда х1(0) = –0,21 рад х2(0) = –0,40 рад, х3(0) = 0 рад/с, х4(0) = 0 рад/с. Численный эксперимент показал, что для нелинейного объекта сохраняется аналог седловой точки, имеющей место в аппроксимирующей линейной игре. В частности, было установлено (с точностью до третьего знака, когда δ = 0,01) совпадение цены игры с величиной гипотетического рассогласования ε0, постоянство функции ε0 вдоль движения, порожденного оптимальными управлениями, ее монотонное убывание, если второй игрок единолично уклоняется от оптимального управления и монотонное возрастание, если единолично уклоняется первый игрок. Соответствующие графики приведены на рис. 3. Из равенства ε(t0, x0) = 0 следует, что даже при самой неблагоприятной реализации помехи схват можно вернуть на базовую траекторию в момент времени ϑ, если пользоваться оптимальной стратегией первого игрока. Показано также, что единоличное уклонение игрока от оптимальной стратегии приводит к ухудшению его результата в игре.
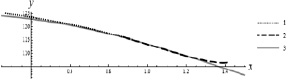
Рис. 2. Траектория движения схвата:1 – движение схвата после его возвращения на базовую траекторию; 2 – траектория схвата, отвечающая времени перевода ϑ = 0,5; 3 –базовая траектория движения схвата
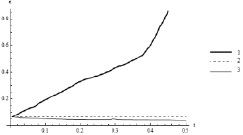
Рис. 3. График функции ε0(t): 1 – при единоличном уклонении первого игрока; 2 – при оптимальных управлениях; 3 – при единоличном уклонении второго игрока
Рецензенты:
Яковлев В.И., д.ф.-м.н., профессор, декан механико-математического факультета, зав. кафедрой процессов управления и информационной безопасности, Пермский национальный исследовательский университет, г. Пермь;
Галкин В.Д., д.т.н., профессор, декан инженерного факультета, Пермская государственная сельскохозяйственная академия им. академика Д.Н. Прянишникова, г. Пермь.
Работа поступила в редакцию 07.05.2013.