Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Эффективность работы торгово-закупочного предприятия во многом зависит от качества планирования закупок и продаж: с одной стороны, в условиях конкуренции необходимо иметь в наличии товары для удовлетворения запросов покупателей, с другой стороны, методика планирования должна быть оптимизирована с точки зрения минимизации остатка товаров на складе. Опыт показывает, что если вопросу планирования закупок и продаж не уделяется должного внимания, то неизбежно возникает избыток по одним товарам и дефицит по другим. Отсутствие необходимых товаров приводит к потере клиентов, а чрезмерное накопление товарных запасов – к перегрузке складских ёмкостей и лишним затратам. Выбор в пользу определенной методики планирования должен осуществляться в зависимости от стратегии, вида деятельности и масштабов предприятия. В частности, на решение этой задачи ориентированы известные технологии планирования MRP, MRP II и т.д. [1, 6].

В основу большинства существующих методик автоматизированного планирования положен ретроспективный анализ данных о продажах, который подразумевает сбор данных за прошедшие периоды и их экстраполяцию. Так, одним из наиболее распространенных способов планирования закупок и продаж является нахождение тренда за предшествующие периоды и принятие полученной величины в качестве опорного значения для необходимых закупок. Если на основе тренда дальнейшее планирование производится полностью автоматически, без участия менеджера (например, информационной системой), то такое планирование может приводить к неадекватному увеличению загрузки склада и значительному количеству отказов клиентам. С другой стороны, возложение задачи планирования большого количества номенклатурных позиций только на менеджеров, без автоматизации процесса, приводит к чрезмерной нагрузке на персонал.

Решение проблемы разделения функций человека и машины в задаче планирования возможно за счет учета стабильности продаж той или иной номенклатурной позиции. Продажи по стабильным номенклатурным позициям возможно с высокой достоверностью планировать автоматически. Те же позиции, по которым продажи нестабильны, требуют участия менеджера с его опытом и интуицией. Все это является побудительным мотивом разработки такой методики планирования, и, соответственно, модели информационной системы, которая бы позволяла автоматизированно выделять номенклатурные позиции, характеризующиеся той или иной достоверностью планирования. В частности, такая методика была описана в работах [4, 5], где рассматривается четырехуровневая модель экспертной оценки достоверности планирования с цветовой интерпретацией, которая позволяет проинформировать менеджера о том, для каких номенклатурных позиций автоматизированное планирование продаж достоверно, а для каких необходима «интуитивная», «ручная» корректировка полученных данных.

Настоящая работа посвящена исследованию методики планирования продаж [4, 5] на данных реального предприятия, анализу её эффективности и демонстрации границ применимости.

Модельные представления задачи

В работах [4, 5] рассматривается модель изменения значения объёма продаж X во времени, которая может быть выражена формулой:

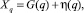
где G(q) – функция, выражающая детерминированный закон эволюции величины X (тренд) в зависимости от момента времени с номером q; η(q) – случайная величина, характеризующая отклонение фактического значения показателя от его тренда (здесь и далее будем считать, что η(q) – некоррелированная случайная величина с нулевым математическим ожиданием).

Функция G(q) может быть использована для экстраполяции значений показателя . Анализ свойств может быть положен в основу оценки достоверности планирования.

Для компаний, чья деятельность является устоявшейся, функцию тренда с большой вероятностью можно считать константой, то есть G(q) = p0. При этом значение планируемого показателя равно константе плюс случайная погрешность: Xi = p0 + ηi;

Оценки среднего значения и среднеквадратичного отклонения показателя X могут быть выражены следующим образом:

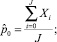
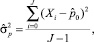
где J – количество моментов времени, участвующих в оценке.

Достоверность экстраполяции показателя X оценивается дискретным набором значений на основании истинности трёх условий.

Условие 1. Величины Xi лежат близко к своему среднему значению, то есть 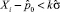для всех i, где k – заданный параметр ширины доверительного интервала.

На рис. 1, a приведен пример, когда условие 1 истинно, а на рис. 1, b условие 1 ложно. Здесь изображены данные о продажах за 7 периодов и границы доверительного интервала 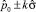(пунктирной линией). На рис. 1, a видно, что экстраполируемые значения не выходят за границы доверительного интервала; это означает, что продажи можно считать стабильными. На рис. 1, b линия графика, иллюстрирующая объем продаж, выходит за верхние границы доверительного интервала в двух точках (в седьмом и в третьем периоде); это говорит о том, что продажи нестабильные.

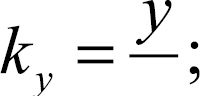
Рис. 1. Динамика продаж при: (а) истинности условия 1, (b) ложности условия 1

Условие 2. Экстраполируемые значения Xi с большой степенью достоверности не равны 0, то есть 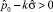, где k – заданный параметр ширины доверительного интервала.

На рис. 2, а приведен пример, где условие 2 истинно: нижняя граница доверительного интервала выше оси абсцисс. Это означает, что в планируемый период продажи по выбранной номенклатурной позиции будут иметь место. Рис. 2, b иллюстрирует иную ситуацию – нижняя граница доверительного интервала ниже оси абсцисс. Это означает, что данных для достоверного планирования недостаточно.

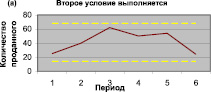
Рис. 2. Динамика продаж при: (а) истинности условия 2, (b) ложности условия 2

Условие 3. Xi > 0 для всех i, то есть среди Xi не встречаются нулевые значения.

Истинность этого условия означает, что периодичность анализа данных выбрана правильно. В частности, если продажи некоторой номенклатурной позиции имеют место лишь раз в месяц, то не имеет смысла принимать период для расчетов и прогнозирования равным неделю. В случае, если условие 3 ложно, то периодичность анализа данных следует увеличить.

Рис. 3, а иллюстрирует ситуацию, условие 3 истинно, то есть нулевых значений продаж нет. Линия графика расположена в пределах доверительного интервала и не пересекает ось абсцисс – периодичность задана корректно. На рис. 3, b объем продаж в двух периодах (втором и шестом) равен 0, это говорит о том, что некорректно выбрана периодичность анализа данных.

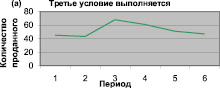
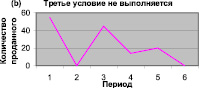
Рис. 3. Динамика продаж при: (а) истинности условия 3, (b) ложности условия 3

Данные условия проверяются для каждой позиции номенклатуры, а затем принимается решение о достоверности планирования по совокупности значений условий (табл. 1). Например, если для какой-либо номенклатурной позиции все три условия истинны, то автоматизированное планирование продаж по такой номенклатурной позиции будет достоверным («зеленый» уровень), и не требует ручной корректировки, а если условие 3 – ложно, то по такой номенклатурной позиции автоматизированное планирование будет недостоверным («красный» уровень) и требует вмешательства менеджера.

Таблица 1

Представление степени достоверности оценки планирования

Предложенная цветовая интерпретация представляется удобной для практики, когда нужно наглядно проинформировать менеджера о том, для каких номенклатурных позиций автоматизированное планирование продаж достоверно («зелёный» уровень), а для каких (возможно) необходима «интуитивная», «ручная» корректировка полученных данных.

Настройка предлагаемой системы оценки достоверности планирования состоит в задании значения параметра k. Он должен быть выбран таким образом, чтобы минимизировать функционал:

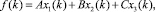(1)

где f(k) – суммарные затраты, складывающиеся из:

1. Недополученной выручки – Ax1(k), где A – сумма недополученной выручки на одну единицу отказов, x1(k) – количество отказов покупателям из-за отсутствия товара на складе, вычисляемое по формуле:

x1(k) = xf – xp,

где xf – фактические продажи; xp – планируемое значение продаж на указанный период.

2. Издержек на хранение складских остатков – Bx2(k), где B – стоимость хранения единицы товара, x2(k)– количество товаров, находящихся на складе, рассчитываемое по формуле:

x2(k) = xp – xf,

где xf – фактические продажи; xp – планируемое значение продаж на указанный период.

3. Затрат на ручное планирование тех позиций номенклатуры, которые не попали в группу автоматически планируемых показателей – Cx3(k), где C – затраты, возникающие в связи с планированием вручную для одной номенклатурной позиции, x3(k) – число планируемых вручную номенклатурных позиций, которое можно подсчитать по формуле:

x3(k) = N – m,

где N – общее число номенклатурных позиций; m – число номенклатурных позиций, для которых осуществляется автоматическое планирование (истинны все три условия).

Значения коэффициентов A, B и C в формуле (1) для разных торгово-закупочных предприятий различны. Поэтому настройка предлагаемой системы оценки достоверности планирования должна производиться для каждого предприятия индивидуально. Реализация такой настройки была рассмотрена на примере реальных данных о динамике продаж за полтора года по двум тысячам номенклатурных позиций в крупной компании, занимающейся торговлей автозапчастями.

Результаты математического моделирования

В процессе моделирования было спланировано количество продаж на период для каждой номенклатурной позиции и проведено сравнение спрогнозированных величин с реальными продажами.

В результате была численно выявлена зависимость (табл. 2) между значением параметра k, характеризующего ширину доверительного интервала и величинами доли отказов покупателям, доли товаров на хранении и доли номенклатурных позиций, планируемых вручную. Так, при k, равном 0,5, доля показателей, планируемых вручную составляет 47,3 %, а при значении k = 1,5 она уменьшается до 38,4 % (табл. 2). С увеличением значения k также снижается доля отказов покупателям и растет доля загрузки склада. При k, равном 0,5, доля отказов покупателям составила 16,54 %, а загрузка склада 8,54 %, а при k, равном 1,5, доля отказов снизилась в три раза и составила 5,55 %, а загрузка склада выросла до 25,13 % (табл. 2).

Таблица 2

Изменение показателей в зависимости от значения k

Тот факт, что функции x1(k), x2(k), x3(k) монотонны, и среди них есть как возрастающие, так и убывающие, означает, что существует минимум функционала (1). Следовательно, может быть выбрано оптимальное значение параметра k, различное для различных значений коэффициентов A, B и C, то есть учитывающее специфику конкретного предприятия.

Заключение

Предлагаемая методика планирования продаж была реализована и успешно внедрена на целом ряде предприятий в виде обработки платформы «1С: Предприятие 8» [3], предназначенной для использования с типовыми конфигурациями «Управление торговлей» и «Управление производственным предприятием». На рис. 4 показан внешний вид одного из вариантов интерфейса этой обработки. Пользователь может выбирать период и периодичность планирования, группу номенклатуры планируемых товаров. Достоверно планируемые продажи выделяются белым цветом. Те же номенклатурные позиции, которые требуют участия менеджера, выделяются желтым, оранжевым или красным цветом.

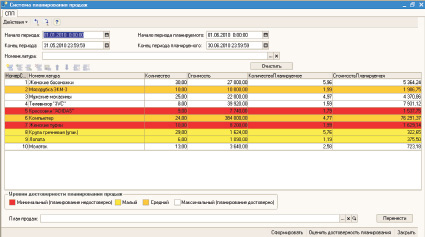
Рис. 4. Обработка платформы «1С: Предприятие 8», реализующая предложенную методику планирования

Несмотря на то, что описанная методика планирования ориентирована на стабильно продаваемые в течение года товары, она может быть распространена и на сезонные товары в том случае, если для них идентифицирована функция тренда G(q) [2].

Рецензенты:

Мазелис Л.С., д.э.н., директор Института информатики, инноваций и бизнес-систем Владивостокского государственного университета экономики и сервиса Минобразования РФ, г. Владивосток;

Кривошеев В.П., д.т.н., профессор кафедры информационных систем и прикладной информатики Владивостокского государственного университета экономики и сервиса Минобразования РФ, г. Владивосток.

Работа поступила в редакцию 07.05.2013.