При движении воды по трещинам пород, содержащих растворимые включения, происходит увеличение раскрытия трещин за счет растворения их стенок. Процесс выноса солей включает как диффузионный транспорт их от поверхности растворения, так и конвективный перенос фильтрующимся потоком. Рассмотрим процесс для наиболее простой схемы одиночной заполненной дисперсным материалом трещины длиной l и шириной 2h; скорость фильтрации считается постоянной и равной v (рисунок). Такого рода задача была исследована А.Н. Патрашевым [5] для условий стационарной диффузии и при пренебрежении диффузионным переносом в направлении конвекции. Считалось также, что коэффициент диффузии одинаков по всем направлениям. Следующее аналитическое решение, свободное от указанных допущений, приведено в работе [2].
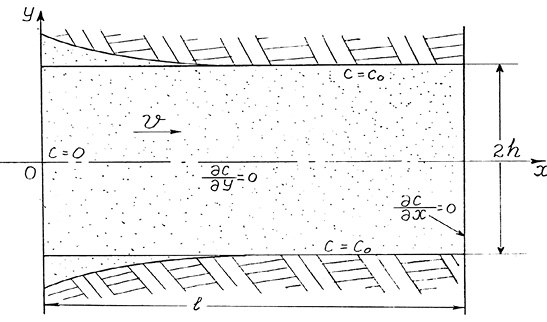
Расчетная схема растворения заполненной трещины
В связи с тем, что v = const, коэффициенты продольной и поперечной конвективной диффузии D1 и D2 также будут постоянными, но различными по величине. Процесс растворения и выноса солей из трещины в таких условиях будет описываться уравнением нестационарной конвективной диффузии в прямоугольной области 0 ≤ x ≤ l, 0 ≤ y ≤ 2h:
(1)
с краевыми условиями:
C(x,y,0) = C(x,0,t) = C0; (2)
(3)
. 
(4)
Применяя к (1) интегральное преобразование Лапласа по переменной t с учетом начального условия (2), получим
(5)
причем
,
где p – параметр преобразования.
Граничные условия (2)–(4) также могут быть представлены в форме изображений:
(6)
(7)
Дальнейшее упрощение хода решения задачи может быть достигнуто путем использования конечного синус-преобразования Фурье по переменной у в форме
.
При этом параметр преобразования может принимать ряд значений, определяемых из уравнения cosλnh = 0, т. е.
(8)
Определив изображения постоянной 
и второй производной 
, включающие граничные условия (6), получим следующее одномерное уравнение для u(x, λn, p):
(9)
Это уравнение должно решаться при граничных условиях
(10)
Представим общее решение (9) в виде
(11)
где
Подстановка (11) в условия (10) позволяет определить постоянные
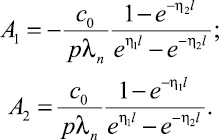
С учетом этих значений постоянных частное решение (9) записывается в виде
(12)
где 
Обратный переход к функции с осуществляется по формуле обращения
Имея в виду, что
получим
(13)
Переход к оригиналу в последнем выражении производится по теореме разложения, что дает окончательное выражение для распределения концентраций в сечении трещины. Опуская промежуточные выкладки, представим это выражение в таком виде:
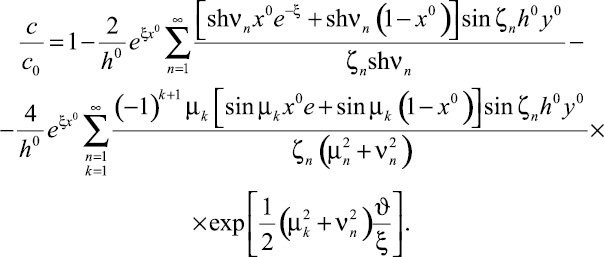(14)
Здесь
– критерий Пекле; 
– критерий Струхаля или кратность обмена жидкости в трещине.
В этих обозначениях перепишем уравнение (1) в следующем виде [1]
(15)
Умножая обе части уравнения (15) на l2/D1, получим
или
(16)
где 
C = C/C0.
Для получения стационарного распределения концентраций в трещине уравнение (16) решаем разностным методом, называемым продольно-поперечной разностной схемой. В этой схеме переход от слоя n к слою n + 1 осуществляется в два этапа. На первом этапе определяют промежуточные значения 
из системы уравнений
(17)
а на втором этапе, пользуясь найденными значениями Yij, находят 
из системы уравнений
(18)
Алгоритм решения уравнений (17) и (18). Перепишем уравнение (17) в виде
,
(19)
где
Уравнение (19) решается при каждом фиксированном j = 1, 2,..., N2 – 1 методом прогонки по переменному i. Чтобы применить прогонку, надо знать граничные значения 
В данном случае
, 
. После того как все 
найдены, решается уравнение (18). Переписывая это уравнение подробнее:
(20)
где
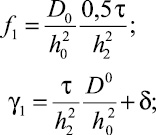
видим, что при каждом фиксированном i = 1, 2,...N1 – 1 его можно решить с помощью одномерной прогонки. Граничные условия в данной задаче 
, 
По приведенному алгоритму для определения распределения концентраций по трещине составлена и отлажена программа на языке ТPascal 7.1.
В таблице приведены численные результаты расчета распределений концентраций раствора в заполненной трещине по указанной программе в сопоставлении с численными результатами, полученными по методу А.С. Малышева.
Распределение концентраций раствора в заполненной трещине при h0 = 0,1, D0 = 0,1, x = 1
|
y0\x0 |
По методу А.С. Малышева |
По предлагаемому методу |
||||||||||
|
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
|||
|
0,0 0,2 0,4 0,6 |
0,0 0,0 0,0 0,0 |
1,0 0,896 0,658 0,591 |
1,0 0,935 0,857 0,805 |
1,0 0,927 0,869 0,810 |
1,0 0,831 0,695 0,603 |
0,0 0,0 0,0 0,0 |
1,0 0,795 0,646 0,614 |
1,0 0,943 0,866 0,794 |
1,0 0,891 0,786 0,715 |
1,0 0,827 0,712 0,660 |
||
Сравнительный анализ численных результатов показывает удовлетворительное соответствие между полученными численными результатами по приведенной программе и результатами, полученными по методу А.С. Малышева.
Стационарное распределение концентраций в трещине (при ϑ → ∞) определяется зависимостью (14) без последнего члена [2].
В тех случаях, когда скорость фильтрации v значительна, коэффициент конвективной диффузии может определяться из соотношения D1,2 = λ1,2v. Критерий Пекле, в свою очередь, может быть представлен в виде ξ = l/2λ1. Так как параметр λ1 по величине близок к среднему размеру зерен заполнителя трещины, представляет интерес получение зависимостей, пригодных при больших значениях критерия Пекле (x ≥ 10). Оценивая для этого аргумент гиперболических функций в (13), найдем, что в области 0,1 < х0 < 0,9 с незначительной погрешностью можно принимать shz = ez/2. Тогда (13) упрощается и имеет вид
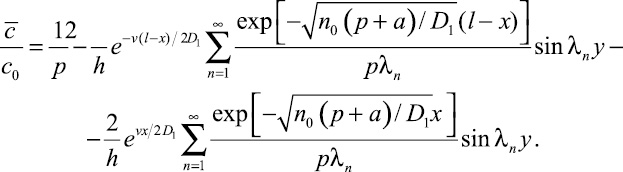(21)
Переход к оригиналу и введение принятых безразмерных величин дает следующую зависимость для распределения концентраций при больших значениях критерия Пекле (x ≥ 10).
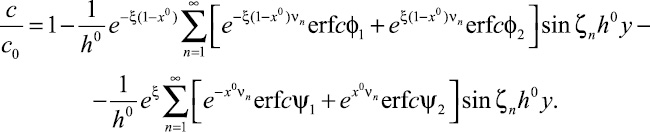(22)
Здесь
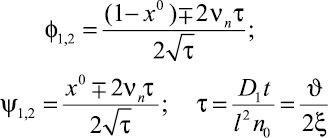
– диффузионный критерий Фурье.
Из выражений (14) и (22) можно определить диффузионный поток солей от растворяющейся стенки трещины и, следовательно, приращение раскрытия трещины 2d в любом ее сечении на некоторый момент времени t. Очевидно, что
(23)
Подставляя (14) в (23), получим после некоторых преобразований следующую зависимость для d:
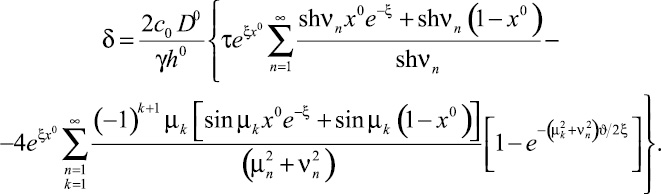(24)
Для оценки интенсивности раскрытия трещины при растворении ее стенок удобно рассматривать средние по длине трещины приращения раскрытия. Из (24) для этой цели может быть получено выражение
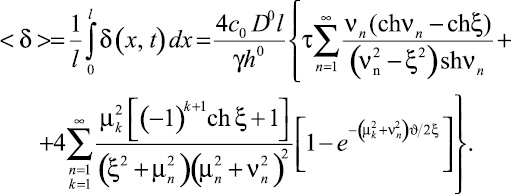(25)
Имея в виду, что при больших значениях ξ можно положить 
, а также заменяя гиперболические функции показательными 
, получим для стационарного режима растворения
(26)
Величина раскрытия трещины в процессе растворения
, (27)
определяемая по зависимости (24), не остается постоянной, а меняется как по длине трещины, так и во времени. Следовательно, задача, рассмотренная выше при h = const, дает достаточно точные результаты только при δ < 0,2h. Если это условие не соблюдается, расчет должен проводиться в две стадии. Сначала для заданного времени t по (25) или (26) определяется среднее раскрытие трещины <2h>, которое затем подставляется во все итоговые зависимости. Этот прием позволяет приближенно учесть изменение размеров трещины в процессе растворения.
Рецензенты:
Агаханов Э.К., д.т.н., профессор, зав. кафедрой «Автомобильные дороги, основания и фундаменты», ФГБОУ ВПО «Дагестанский государственный технический университет», г. Махачкала;
Баламирзоев А.Г., д.т.н., профессор кафедры прикладной математики Махачкалинского филиала МАДИ, г. Махачкала.
Работа поступила в редакцию 22.04.2013.