Обоснование безопасности атомных электрических станций (АЭС) осуществляется с помощью расчетных анализов режимов работы АЭС программными средствами (кодами). Важное место в этом процессе занимают коды, описывающие нестационарную теплогидравлику в контуре охлаждения реакторных установок (РУ). К настоящему моменту в России и за рубежом накоплен большой опыт разработки и валидации теплогидравлических расчетных кодов, используемых для моделирования течения водяного теплоносителя в контурах реакторных установок.
В настоящее время все основные современные теплогидравлические коды используют карты режимов течения двухфазного потока, выделяющие типичные структуры течения двухфазного потока в любой локальной области в зависимости от истинного объемного паросодержания и массовой скорости среды (пузырьковое течение, дисперсно-кольцевое течение и т.п.) На их основе осуществляется выбор корреляций, описывающих взаимодействия между фазами и каждой фазы со стенками каналов. При этом величина межфазной поверхности, необходимая для вычисления межфазного взаимодействия, определяется по текущим значениям характеристик фаз (скорости, объемном паросодержании и т.д.), исходя из которых рассчитываются размеры дисперсных включений (пузырьки, капли) по критериям типа критерия Вебера и площади межфазной поверхности.
Этот подход имеет следующие недостатки [7]: невозможность учета динамической смены режимов, эффектов, связанных с входным потоком или с формированием течения, искусственные разрывы значений параметров при смене режимов и т.д.
В связи с этим в последние годы появилось целое направление экспериментальных и теоретических работ по более точному определению площади межфазной поверхности [5, 6, 10]. В этих работах исследуются различные механизмы коалесценции или фрагментации дисперсных образований в двухфазных потоках и в соответствии с ними разрабатываются количественные соотношения, описывающие скорость изменения межфазной поверхности вследствие этих процессов. Полученные соотношения как источниковые (стоковые) члены вводятся в уравнение переноса межфазной поверхности, которое следует из уравнения, описывающего динамику распределения дисперсных образований по пространству и их размерам.
Уравнение переноса межфазной поверхности, учитывающее процессы коалесценции и фрагментации, а также фазового перехода и присоединенное к основной системе уравнений сохранения, позволяет непосредственно рассчитывать площадь межфазной поверхности в любой точке рассматриваемого течения в произвольный момент времени, не прибегая к карте режимов течения и критериальным соотношениям, что является ее несомненным преимуществом.
Цель работы: разработка теплогидравлического кода CATEQ, использующего уравнение переноса межфазной поверхности, и численное моделирование с помощью этого кода эксперимента по измерению межфазной поверхности.
Материал и методы исследования
Код CATEQ создан на базе кода STEG [1, 2, 3], предназначенного для трехмерных расчетов двухфазной пароводяной среды в областях сложной геометрии с учетом внутренних конструкций (например, в парогенераторах). Код CATEQ реализует двухскоростную двухтемпературную модель пароводяной среды. Настоящая версия кода CATEQ использует модели межфазного взаимодействия и взаимодействия со стенками, применяемые в коде STEG и подробно изложенные в [1].
Для возможности непосредственного моделирования водо-воздушных течений в код CATEQ (в отличие от кода STEG) в качестве газовой фазы наряду с водяным паром был внедрен неконденсирующийся газ с термодинамическими и теплофизическими свойствами воздуха.
Основной особенностью кода CATEQ является включение в состав системы определяющих уравнений уравнения переноса межфазной поверхности. Это уравнение, наиболее подробный вывод которого представлен в [7], имеет следующий вид:
![]()
где ai – концентрация площади межфазной поверхности, м–1; υi – скорость движения межфазной поверхности, м/с; υg – скорость движения паровой фазы, м/с; a – объемная доля воздуха (истинное объемное газосодержание). Параметр ϕj описывает изменение межфазной поверхности в ходе определенного (j-го) процесса взаимодействия газовых пузырьков. В (1) опущены члены, описывающие фазовый переход, поскольку далее в статье рассматриваются только водо-воздушные системы.
Уравнение (1) имеет вполне ясную физическую трактовку. Второй член левой части этого уравнения описывает изменение площади межфазной поверхности из-за ее переноса течением двухфазной среды. Первый член правой части (1) учитывает изменение площади межфазной поверхности вследствие изменения объемного газосодержания двухфазной среды из-за изменения давления по ходу течения. Значение второго члена правой части (1) объяснено выше. Первый член левой части уравнения (1) вычисляет суммарное изменение площади межфазной поверхности во времени вследствие всех рассматриваемых процессов.
В настоящее время выделяют три основных процесса взаимодействия газовых образований (пузырьков) в пузырьковом потоке, приводящих к изменению площади межфазной поверхности [9, 10]:
коалесценция пузырьков вследствие хаотичных (случайных) столкновений, вызванных турбулентными пульсациями в жидкой фазе;
слияние (коалесценция) с пузырьком – лидером пузырьков, ускоренно движущихся в его следе;
дробление пузырьков под воздействием турбулентных вихрей в жидкости.
Для описания этих процессов взаимодействия пузырьков в коде CATEQ были использованы их математические модели, представленные в [7].
В коде CATEQ уравнение переноса межфазной поверхности (1) аппроксимировалось явным образом. Было сделано достаточно естественное предположение [7], что скорость движения межфазной поверхности равна скорости газовой фазы.
Результаты исследования и их обсуждение
С помощью кода CATEQ было выполнено численное моделирование эксперимента 2–9 [8] (в [9] этому эксперименту был присвоен номер 2–5), проведенного в рамках экспериментальных исследований переноса межфазной поверхности в вертикальных подъемных адиабатных пузырьковых течениях водо-воздушной смеси. Использовались две круглые трубы с внутренними диаметрами 25,4 и 48,3 мм длиною около 3 м. Эксперименты проводились при атмосферном давлении, приведенные скорости воздуха менялись от 0,041 до 1,790 м/с, воды – от 0,262 до 5,1 м/с. С помощью кондуктометрических датчиков, установленных в трубе на трех высотных отметках, измерялись концентрация межфазной поверхности и объемная доля воздуха (истинное объемное газосодержание).
Эксперимент 2–9 был выбран потому, что в [8, 9] только для него приведена наиболее полная информация, минимизирующая неопределенности входных данных при его численном моделировании.
В качестве граничных условий задавались расходы фаз на входе в трубу (экспериментальные значения приведенных скоростей воздуха и воды равнялись 0,538 и 5,1 м/с, соответственно).
Численное моделирование этого эксперимента кодом CATEQ проводилось в одномерном приближении на расчетной сетке с использованием 34 ячеек по длине трубы. Шаг по времени составлял 0,02 с. Проведенные методические расчеты показали, что при таком разбиении получающееся численное решение не зависит от параметров пространственно-временной сетки.
Результаты расчета в сравнении с экспериментальными результатами приведены на рис. 1–3.
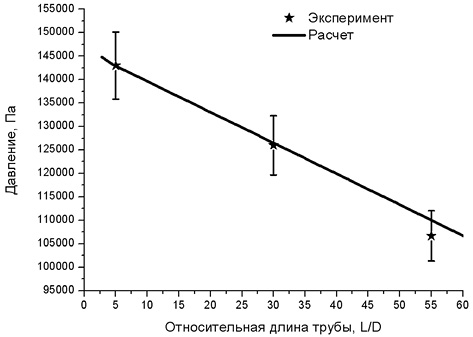
Рис. 1. Сопоставление экспериментальных данных по распределению давления вдоль трубы и результатов расчета кодом CATEQ. Вертикальные отрезки показывают погрешности эксперимента
Сравнение экспериментальных и расчетных данных по перепаду давления (рис. 1) показывает их достаточно хорошее совпадение. Расчетный перепад давления на длине трубы немного меньше экспериментального.
Распределение объемной доли воздуха по длине трубы представлено на рис. 2. Расчетная кривая расположена немного ниже экспериментальных точек, что, видимо, связано с заниженным расчетным перепадом давления на трубе, вследствие чего расширение воздуха в верхней части трубы воспроизводится кодом CATEQ не в полной мере.
Анализ экспериментальных данных по концентрации межфазной поверхности (см. рис. 3) показывает, что после нижней измерительной отметки эта величина в середине трубы (средняя отметка) возрастает примерно на 20 %. Согласно [7], для этих параметров пузырькового течения дробление пузырьков практически отсутствует. Следовательно, увеличение площади межфазной поверхности осуществляется вследствие расширения воздуха на отрезке между нижним и средним измерениями. Процессы коалесценции на этом отрезке течения потока также малы и не вносят заметный вклад в изменение площади межфазной поверхности. Однако при переходе к верхней измерительной отметке концентрация площади межфазной поверхности падает на 8 %, что можно объяснить существенной интенсификацией процессов коалесценции при параметрах пузырькового течения, реализующихся на отрезке между средним и верхним измерениями.
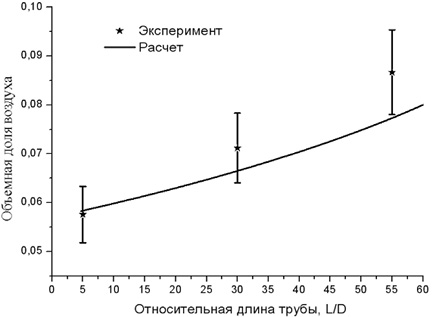
Рис. 2. Сопоставление экспериментальных данных по объемной доле воздуха и результатов расчета кодом CATEQ. Вертикальные отрезки показывают погрешности эксперимента
Результаты расчета кодом CATEQ концентрации площади межфазной поверхности (см. рис. 3) достаточно неплохо совпадают с опытными данными на крайних измерительных отметках, однако для средней отметки в расчете не был получен максимум этой величины – расчетная кривая монотонно возрастает. Это обстоятельство свидетельствует о занижении математическим моделями коалесценции пузырьков (2), (3) интенсивности коалесценции для данных условий пузырькового течения.
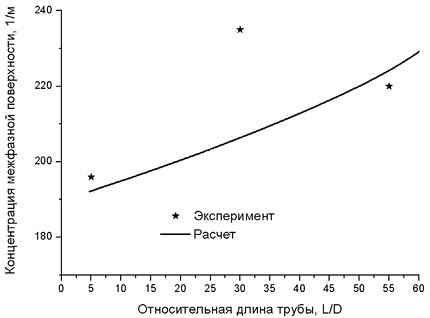
Рис. 3. Сопоставление экспериментальных данных по концентрации межфазной поверхности и результатов расчета кодом CATEQ. Вертикальные отрезки показывают погрешности эксперимента
Выводы
В данной работе было выполнено расчетно-экспериментальное исследование адиабатного пузырькового водо-воздушного потока в вертикальной трубе.
Расчет экспериментов выполнялся с помощью двухжидкостного теплогидравлического кода CATEQ с уравнением эволюции межфазной поверхности, имплементированным в математическую модель кода.
Результаты расчетов (рис. 1–3) показали, что код удовлетворительно воспроизводит распределение давления и объемной доли воздуха по высоте трубы. Расчетная величина концентрации межфазной поверхности хорошо совпадает с экспериментальными значениями, немного хуже – на средней высотной отметке. Усовершенствование кода CATEQ требует расширения спектра экспериментальных данных, используемых для его валидации.
Рецензенты:
Елкин И.В., д.т.н., ведущий научный сотрудник Национального исследовательского центра «Курчатовский институт», г. Москва;
Якуш С.Е., д.ф.-м.н., ведущий научный сотрудник лаборатории термогазодинамики и горения, ФГБУН «Институт проблем механики им. А.Ю. Ишлинского РАН», г. Москва.
Работа поступила в редакцию 08.04.2013.



