Нормальное распределение случайной величины имеет неограниченную область рассеяния. В то же время область значений случайных величин, анализ которых приходится проводить в естествознании, технике и экономике, оказывается конечной. Как следствие, распределения данных случайных величин отличаются от идеализированной модели с неограниченной областью рассеяния. В качестве примеров физических характеристик с ограниченной областью рассеяния можно привести плотность углей, изменяющейся в диапазоне от ρmin до некоторого максимального значения ρmax время безотказной работы группы однотипных приборов, изменяющегося в диапазоне от некоторого минимального значения Tmin до некоторого максимального Tmax и т.д.
Существует два альтернативных подхода к построению математических моделей обсуждаемых случайных величин. Первый подход основан на описании распределения случайной величины с помощью усеченных функций нормального распределения [1]:
![]() (1)
(1)
где 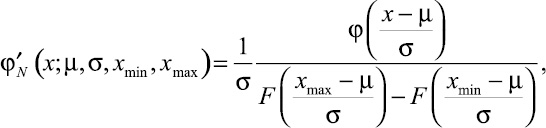
где φ(x) − плотность стандартного нормального распределения N(0, 1); ![]() − функция Лапласа; μ, σ − параметры исходного нормального распределения; xmin < xmax − точки усечения.
− функция Лапласа; μ, σ − параметры исходного нормального распределения; xmin < xmax − точки усечения.
Во втором подходе, базирующемся на работах А. Эйнштейна и М. Смолуховского по теории броуновского движения [7], модель статистического распределения случайной последовательности строится как распределение конечного состояния некоторого случайного процесса без последействия с ограниченной областью рассеяния [3]. Его плотность распределения, являющаяся линейной комбинацией плотностей распределений мнимых источников (рис. 1), описывается следующим выражением [4]:
![]() (2)
(2)
где х0 – положение центра рассеяния в системе координат с началом в центре отрезка [xmin, xmax]; s − СКО случайного процесса при отсутствии ограничения; l = xmax – xmin – размаха области рассеяния; А – нормировочный коэффициент, определяемый из условия
![]() (3)
(3)
![]()
![]()
![]()
где ![]() вычисляются по формулам:
вычисляются по формулам:
![]() (4)
(4)
соответственно функция распределения
![]() (5)
(5)
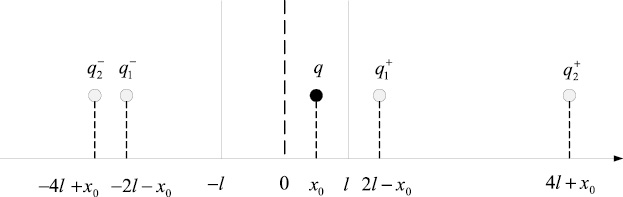
Рис. 1. К вычислению координат фиктивных источников
Результаты сравнительного анализа распределений (1), (2), проведенные в [4], показывают, что при использовании математической модели (1) для описания функции распределения случайной последовательности с ограниченной областью блуждания в зависимости от значений параметров математической модели ошибка может достигать 10 %. В этой связи для аппроксимации распределений случайных величин, область значений которых из физических соображений является ограниченной, следует использовать математическую модель (2), зависящую от следующих 4-х параметров: x0, σ, l = xmax – xmin. Кроме того, при практическом использовании (2) в список параметров модели с неизбежностью приходится вводить еще один параметр – количество мнимых источников Nf, используемых в (2), от которого также будет зависеть точность аппроксимации функции распределения. Таким образом, фактически математическая модель (2) является 5-ти параметрической.
Напомним, что существование решения задачи аппроксимации распределения случайной последовательности обеспечивается теоремой Гливенко [1], в соответствии с которой эмпирическая функция распределения FN(x)
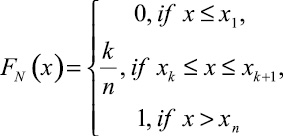
любой упорядоченной по возрастанию совокупности случайных величин ![]()
![]()
при N → ∞ сходится, вообще говоря, к неизвестной истиной интегральной функции распределения ![]()
![]() – вектор параметров. Для случайной величины с ограниченной областью рассеяния
– вектор параметров. Для случайной величины с ограниченной областью рассеяния
![]()
Традиционно вектор параметров находят как решение одной из следующих задач:
![]() (6)
(6)
![]() (7)
(7)
где Ф – тот или иной функционал, вид которого зависит от выбранного критерия близости функций ![]() и
и ![]() . Например, для решения задачи (6) можно использовать метод максимального правдоподобия, задачи (7) – метод наименьших квадратов и т.д.
. Например, для решения задачи (6) можно использовать метод максимального правдоподобия, задачи (7) – метод наименьших квадратов и т.д.
Отметим, что в подавляющем большинстве случаев решение задач (6), (7) сводится к решению некоторой, вообще говоря, нелинейной системы уравнений, которое может быть найдено только численно. При этом точность оценки вектора параметров ![]() оказывается напрямую зависящей от удачного выбора начального приближения
оказывается напрямую зависящей от удачного выбора начального приближения ![]() и области, в которой осуществляется поиск возможных значений координат вектора. В этой связи разработка научно обоснованных рекомендаций по выбору начального приближения и области поиска возможных значений параметров в задаче оценки параметров функции распределения случайной величины с ограниченной областью рассеяния является актуальной.
и области, в которой осуществляется поиск возможных значений координат вектора. В этой связи разработка научно обоснованных рекомендаций по выбору начального приближения и области поиска возможных значений параметров в задаче оценки параметров функции распределения случайной величины с ограниченной областью рассеяния является актуальной.
В статье обсуждаются результаты статистического моделирования методом Монте-Карло случайных блужданий броуновской частицы в ограниченной области рассеяния, позволяющие установить связь между размерами области случайных блужданий и параметрами функции распределения.
Свойства случайных блужданий с неограниченной областью рассеяния
Предваряя обсуждения особенностей случайных блужданий в ограниченной области, напомним, следуя [5], основные свойства случайных блужданий с неограниченной областью рассеяния. В данной одномерной модели случайных блужданий частицы предполагается, что частица в начальный момент времени расположена в точке с координатой x0 = 0. Далее на каждом шаге частица совершает перемещение на величину шага с вероятностью влево или с вероятностью q = 1 – p вправо. Тогда вероятность нахождения частицы через n шагов в точке с координатой x = m∙Pn(m), вычисляется по формуле
![]() (8)
(8)
где n + m n – m − число элементарных смещений (шагов) вправо и влево соответственно. (Здесь, если n – четно, то m тоже четно, и, наоборот, если n – нечетно, то m тоже нечетно). При ![]() (8) принимает следующий вид:
(8) принимает следующий вид:
![]() (9)
(9)
Соотношения (8), (9) с физической точки зрения могут быть истолкованы следующим образом [2]. Предположим, что в начальный момент времени в точке x = 0 имелось большое количество частиц (ансамбль частиц). Далее частицы начинают перемещаться под действием случайных толчков независимо друг от друга. Тогда (8), (9) есть доля частиц, оказавшихся на расстоянии m от начала отсчета.
При больших значениях n выражение (9) в соответствии с локальной теоремой Муавра–Лапласа аппроксимируется следующим выражением:
![]() (10)
(10)
где n – число шагов, совершенных частицей.
Из (10) видно, что при достаточно большом числе шагов распределение координат частицы, совершающей случайные блуждания, описывается нормальным законом распределения.
Зависимость координаты частицы, усредненной по ансамблю частиц, совершающих независимые перемещения, от номера шага перемещения n
![]()
где ![]() N – число частиц в ансамбле для случая x0 = 0 описывается выражением [6]
N – число частиц в ансамбле для случая x0 = 0 описывается выражением [6]
![]() (11)
(11)
для случая x0 ≠ 0 описывается выражением
![]() (12)
(12)
Зависимость квадрата смещения частицы, усредненной по ансамблю частиц, совершающих независимые перемещения, от номера шага перемещения n
![]()
где ![]() N – число частиц в ансамбле, для случая x0 = 0 описывается выражением [6]
N – число частиц в ансамбле, для случая x0 = 0 описывается выражением [6]
![]() (13)
(13)
для случая x0 ≠ 0 описывается выражением
![]() . (14)
. (14)
Если ![]() , выражения (11)–(14) соответственно принимают следующий вид:
, выражения (11)–(14) соответственно принимают следующий вид:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
Из (13), (14), (17), (18) видно, что дисперсия случайного блуждания зависит линейно от числа шагов частицы, совершающей случайные блуждания, что соответствует результату, полученному А. Эйнштейном для броуновского движения, который показал [7], что дисперсия линейно зависит от времени t, что в рассматриваемом случае эквивалентно числу случайных шагов n.
Типичные результаты статистического моделирования случайного блуждания с неограниченной областью рассеяния представлены на рис. 2, 3.
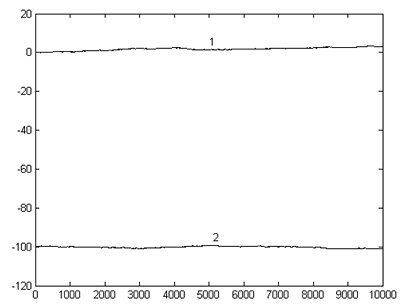
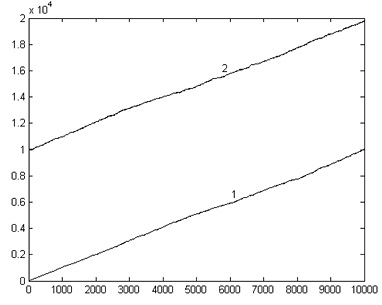
Рис. 2. Графики зависимостей ![]() (слева),
(слева), ![]() (справа) для случая
(справа) для случая ![]() N = 5∙103:1 – x0 = 0; 2 – x0 = –100
N = 5∙103:1 – x0 = 0; 2 – x0 = –100
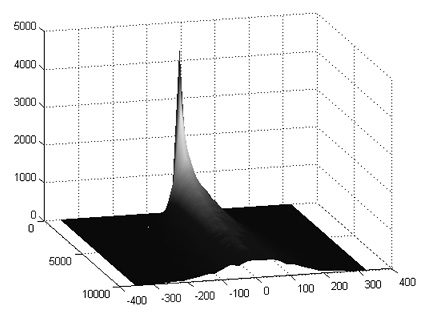
Рис. 3. Поверхность, задаваемая функцией N∙Pn(m)
Из рис. 2 видно, что результаты статистического моделирования согласуются с теоретическими зависимостями, так как для каждого из рассмотренных случаев ![]() а уравнения прямых, аппроксимирующих зависимости
а уравнения прямых, аппроксимирующих зависимости ![]() по методу наименьших квадратов зависимости имеют вид:
по методу наименьших квадратов зависимости имеют вид:
1 – ![]()
2 – ![]()
Полученные результаты, в свою очередь, свидетельствуют о достаточно высоком качестве использованного в статистическом моделировании генератора случайных чисел.
Из рис. 3 видно, что с течением времени происходит расплывание функции N∙Pn(m) в пространстве (по переменной m). При этом ее форма (зависимость от переменной m) не меняется.
Моделирование случайных блужданий частицы в ограниченной области
Блок-схема алгоритма моделирования случайных блужданий в ограниченной области рассеяния [xmin, xmax] представлена на рис. 4.
В данном алгоритме для каждой частицы ансамбля после каждого шага Монте-Карло проводится сравнение текущей координаты частицы xn с координатами левой и правой границ. Если координата точки на очередном шаге xn > xmax, то частицу следует упруго отразить от стенки, поместив ее на расстояние xn – xmax слева от точки xmax:
![]()
Если координата точки на очередном шаге xn < xmin, то частицу следует упруго отразить от стенки, поместив ее на расстояние xmin – xn справа от точки xmin:
![]()
После вычисления траектории блужданий каждой из частиц ансамбля, на каждом шаге Монте-Карло вычисляются ![]()
В соответствии с описанным выше алгоритмом были проведено статистическое моделирования случайных блужданий с ограниченной областью рассеяния, цель которых состояла в выявлении функциональных зависимостей между начальной координатой частицы x0, координатами левой и правой границ области рассеяния и зависимостями ![]() , а также их влияние на вид плотности распределения случайного блуждания.
, а также их влияние на вид плотности распределения случайного блуждания.
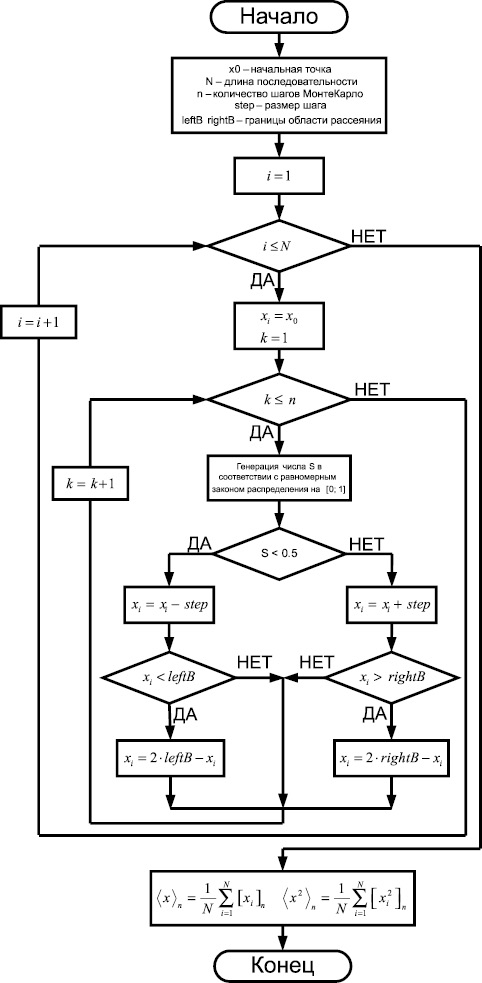
Рис. 4. Блок-схема случайного блуждания в ограниченной области
Рассмотрим результаты статистических исследований, представленные на рис. 5.
Из рис. 5 видно, что случайные блуждания в ограниченной области рассеяния имеют следующие свойства:
1. Для случая x0 = 0 и x2 = –x1 плотность распределения при n → ∞ стремится к равномерному закону распределения с центром в точке x0 = 0 и областью рассеяния 2l = x2 – x1 (рис. 5 а, б).
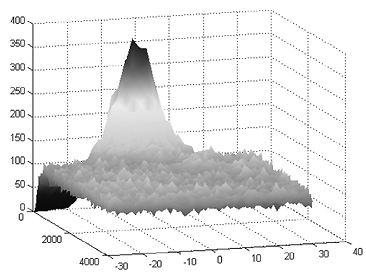
а) Поверхность, задаваемая функцией N∙Pn(m): x0 = 0 x1 = –30 x2 = 30 l = 30 N = 3000, n = 50, 60, ..., 4000
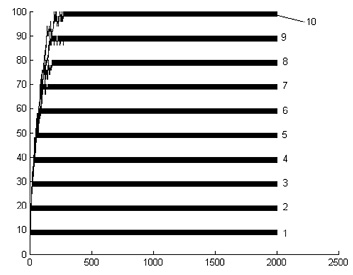
б) Зависимость размаха случайных блужданий от номера шага Монте-Карло: x0 = 0, x2 = –x1, ![]() N = 3000,
N = 3000, ![]()
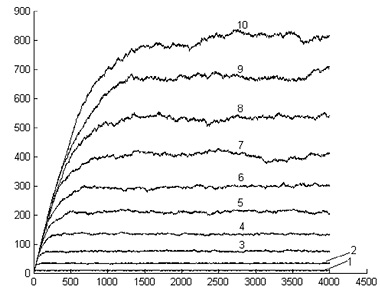
в) Зависимость ![]() : x0 = 0, x2 = –x1
: x0 = 0, x2 = –x1 ![]() N = 3000,
N = 3000, ![]()
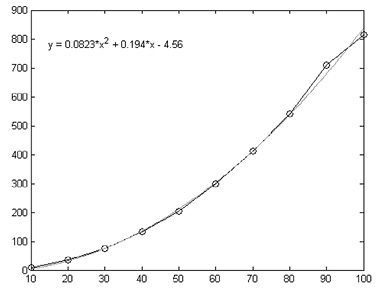
г) Зависимость ![]() от 2l2 x0 = 0 N = 3000
от 2l2 x0 = 0 N = 3000
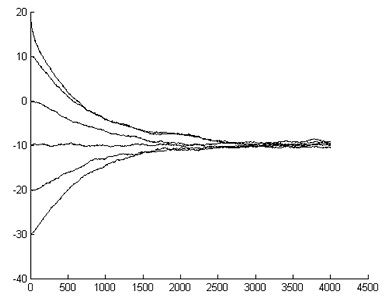
д) Зависимость ![]() : x0 = –30, –20, ..., 20 x1 = –40, x2 = 30, 2l = 70, N = 3000,
: x0 = –30, –20, ..., 20 x1 = –40, x2 = 30, 2l = 70, N = 3000, ![]()
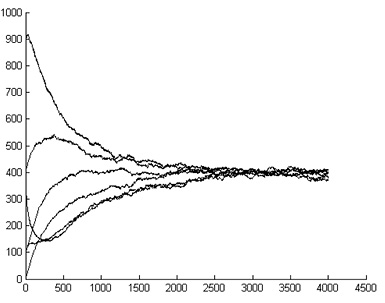
е) Зависимость ![]() : x0 = –30, –20, ..., 20 x1 = –40, x2 = 30, 2l = 70, N = 3000,
: x0 = –30, –20, ..., 20 x1 = –40, x2 = 30, 2l = 70, N = 3000, ![]()
Рис. 5. Результаты статистических исследований
2. Для случая x0 = 0 и x2 = –x1 зависимость ![]() при n → ∞ стремится к некоторому предельному значению, определяемому размером области рассеяния 2l (рис. 5 в, г).
при n → ∞ стремится к некоторому предельному значению, определяемому размером области рассеяния 2l (рис. 5 в, г).
3. Для случая ![]() плотность распределения при n → ∞ вне зависимости от координаты начальной точки x0 стремится к равномерному закону распределения с областью рассеяния 2l = x2 – x1 и средним значением
плотность распределения при n → ∞ вне зависимости от координаты начальной точки x0 стремится к равномерному закону распределения с областью рассеяния 2l = x2 – x1 и средним значением ![]() (рис. 5 д).
(рис. 5 д).
4. Для случая ![]() зависимость
зависимость ![]() при n → ∞ вне зависимости от координаты x0 стремится к некоторому предельному значению, определяемому размером области рассеяния 2l (рис. 5 е).
при n → ∞ вне зависимости от координаты x0 стремится к некоторому предельному значению, определяемому размером области рассеяния 2l (рис. 5 е).
Заключение
Существуют принципиальные отличия между случайными блужданиями с неограниченной областью рассеяния, у которых средний квадрат смещения броуновской частицы, линейно неограниченно увеличивается с течением времени, и ограниченной областями рассеяния, у которых данная величина стремится к некоторому предельному значению, зависящему от размера области случайных блужданий и независящему от точки x0.
Результаты проведенных исследований позволяют дать следующие рекомендации для использования на практике математической модели (5)в задаче аппроксимации распределения случайной последовательности xi, i = 1, M.
1. Нулевое приближении параметра x0 нужно выбирать из отрезка ![]() , где
, где ![]() – минимальное и максимальное значения случайной последовательности xi, i = 1, M.
– минимальное и максимальное значения случайной последовательности xi, i = 1, M.
2. Область поиска истинного значения параметра x0 следует ограничить отрезком ![]() .
.
3. Нулевое приближение ![]() параметра нужно оценивать по 1 экспериментальному значению области рассеяния
параметра нужно оценивать по 1 экспериментальному значению области рассеяния ![]() и зависимости
и зависимости ![]() , полученной на основе статистического моделирования (рис. 5 г).
, полученной на основе статистического моделирования (рис. 5 г).
4. Область поиска истинного значения параметра σ следует ограничить отрезком ![]()
Рецензенты:
Кубланов В.С., д.т.н., доцент, профессор кафедры радиоэлектроники информационных систем, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург;
Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой информационных технологий, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 11.04.2013.



