Анализ динамики современных сложных механических систем, таких как металлургические мостовые краны, представляет острую проблему в силу ее серьезного влияния на техногенную безопасность. Важным аспектом этой проблемы является конструкционная безопасность.
Обобщающее условие анализа и управления безопасностью можно представить в форме
(1) [1, 3].
Выявить отдельные элементы или участки механической системы, которые определяют параметр Р(t), выработать практические меры по исключению опасных резонансных зон – основная цель при совершенствовании и оптимизации параметров надежности конструкции.
Процесс перехода потенциальной энергии в кинетическую движущихся масс и обратно сопровождается возникновением колебаний в системе и динамических нагрузок на ее элементы [8]. Колебательное движение металлургического мостового крана можно описать дифференциальным уравнением в форме Лагранжа следующего вида:
(2)
где φi, 
– перемещение i-го элемента крана и первая производная; Qi – вынужденная внешняя нагрузка в виде изгибающей или какой-либо другой силы; Т – кинетическая энергия свободно колеблющейся системы. При свободных колебаниях принимается [8] нулевое значение правой части формулы (2) (Qi = 0).
(3)
где Ji – параметр инерционности элемента в виде момента инерции или величины массы; П – потенциальная энергия свободно колеблющейся системы:
(4)
где ci – параметр жесткости.
Подставив (4) и (3) в (2) и имея, что
получим
Тогда уравнение (2) примет вид
(5)
Для системы, имеющей n масс, количество уравнений (5) будет равно n. Полученная система дифференциальных уравнений решается известными методами [6]. Частное решение такой системы принимаем в виде
(6)
где Аi – амплитуда колебаний i-й системы; wci – частота свободных колебаний системы; ai – фаза колебаний системы.
Подставив решение в систему дифференциальных уравнений, получим систему однородных дифференциальных уравнений относительно неизвестных амплитуд колебаний. Решая его, получим частотное уравнение свободных колебаний системы относительно неизвестных частот w.
Для такой сложной механической системы, как металлургический кран, применяется матричный метод решения частотного уравнения. Для этого система дифференциальных уравнений n массовой системы записывается в операторном виде:
(7)
где J – диагональная матрица параметров масс элементов крана; С – симметричная матрица коэффициентов жесткости; φ – вектор-столбец перемещений элементов системы.
Анализ динамики сложных механических систем имеет серьезное значение при оценке параметров надежности и безопасности.
Расчетная динамическая схема системы должна удовлетворять двум главным требованиям: во-первых, она должна быть адекватна реальной системе и, насколько это возможно, отражать основные физические свойства исследуемой системы; во-вторых, она должна быть не очень сложной, чтобы решение динамической задачи оказалось не слишком трудоемким [9]. Основу мостового крана представляет металлоконструкция, состоящая из несущих и концевых балок, которые вместе образуют жесткую конструкцию, способную выдерживать приложенные нагрузки.
На следующем этапе анализа динамической расчетной схемы выявляются те участки несущих конструкций и элементов механизмов подъема металлургического мостового крана, которые будут определять динамику всей системы и ее нагруженность, для определения входных и выходных параметров системы.
При выполнении динамических расчетов рассматриваемой механической системы будем исследовать движение конструкции крана, испытывающей внешние механические силовые воздействия, которые возбуждают изгибные колебания в виде линейных перемещений элементов с возникновением перегрузок (амплитуд ускорений) и динамических воздействий на них.
Принятый метод анализа механической системы предполагает получение точного решения дифференциальных уравнений, описывающих ее движение с учетом упругих деформаций, а затем уточнение, разработку и применение вероятностных методов прогнозирующего расчета определяющего параметра P(t) на основании исследования случайного процесса изменения входных параметров.
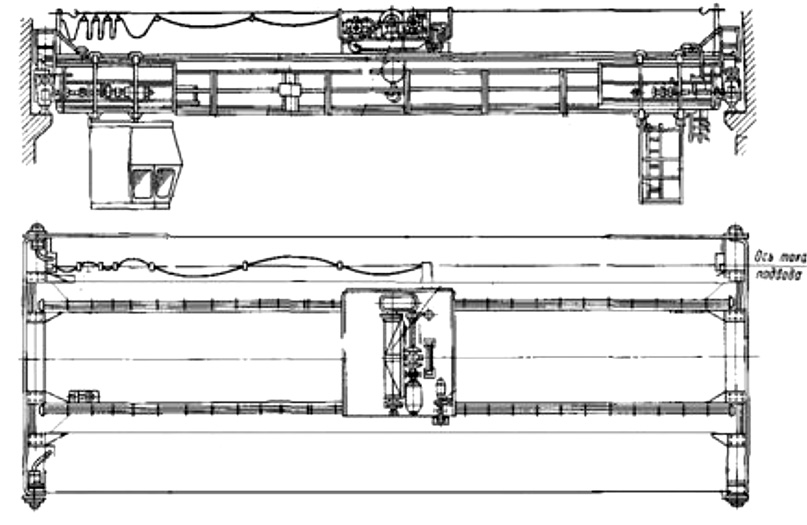
Рис. 1. Общий вид мостового крана
Балки испытывают нагрузки согласно следующей схеме:
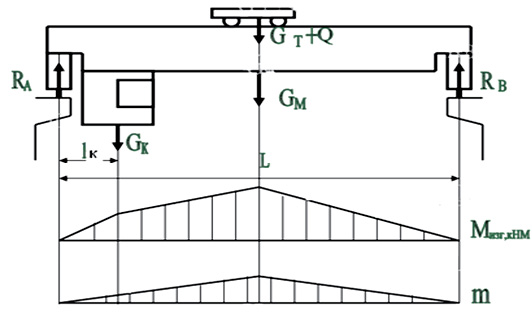
Рис. 2. К построению динамической модели мостового крана
Для достижения поставленной цели используем метод преобразования вероятностей [2, 3, 8]: определяется закон распределения выходных параметров по известному закону распределения вероятности входных параметров. Рассмотрим две случайные величины, связанные функциональной зависимостью: уровень пластической (упругой) деформации и величина действующей нагрузки; статистические характеристики случайной величины У определяются как функции случайного аргумента Х, если задан закон распределения Х. Можно записать:
p(x, t1)dx = p(y, t1)dy, (8)
откуда
(9)
уравнение (9) представляет большой интерес, так как позволяет преобразовать плотности вероятностей входного параметра системы в плотность вероятности выходного параметра.
Таким образом, приведенный анализ динамики и некоторые вопросы оптимизации такой группы объектов, как металлургические мостовые краны, позволяют сформулировать и аналитически оценить уровень пластической (упругой) деформации их основных несущих конструкций в зависимости от величины действующей нагрузки как определяющего параметра при управлении техногенной безопасностью и рисками.
Рецензенты:
Черчинцев В.Д., д.т.н., профессор, заведующий кафедрой промышленной экологии безопасности жизнедеятельности, МГТУ им. Г.И. Носова, г. Магнитогорск;
Корнилов С.Н., д.т.н., профессор, заведующий кафедрой промышленного транспорта, МГТУ им. Г.И. Носова, г. Магнитогорск.
Работа поступила в редакцию 11.04.2013.