Вызванные потенциалы являются ответом головного мозга, на какое-либо внешнее раздражение, проявляющееся в виде низкоамплитудных электрических сигналов на фоне электроэнцефалограммы (ЭЭГ). Наиболее распространёнными типами раздражений, применяемых в медицинской диагностике, являются: звуковые сигналы, световые вспышки и раздражение нервных окончаний конечностей электрическим током небольшой амплитуды. Получаемые при этом реализации вызванных потенциалов называются, соответственно, слуховые, зрительные и соматосенсорные вызванные потенциалы.
Основное отличие ВП от ЭЭГ в том, что амплитуда ЭЭГ в десятки раз превышает амплитуду ВП. Поэтому зарегистрировать ВП методами, применяемыми для регистрации ЭЭГ невозможно. Традиционным методом, применяемым для регистрации и выделения ВП, является когерентное усреднение, основанное на суммировании реализаций ВП при большом количестве подаваемых стимулов. Но данный метод имеет такие существенные недостатки, как большое время регистрации и подавление высокочастотных компонент ВП за счёт не идентичности реализаций.
Выделяемый сигнал, как и помехи, могут быть представлены случайными процессами. Исследования показали, что значения напряжения отсчётов реализаций распределены не строго по нормальному закону. При этом распределение помех, включающих в себя ЭЭГ, на фоне которой осуществляется регистрация ВП и шумы измерения, может быть приближённо описано как нормальное. Для уменьшения времени выделения и повышения достоверности обработки в работе предлагается использовать методы статистической радиотехники и теории смесевого представления сигналов и помех, позволяющие аппроксимировать физически реализуемые случайные процессы смесью гауссовских распределений с любой заданной наперёд точностью.
Для описания реализаций ВП в виде смеси необходимо провести классификация выделяемых сигналов. В первую очередь ВП можно классифицировать по типу подаваемого раздражения на зрительные (ЗВП), звуковые или слуховые (СВП) и соматосенсорные (ССВП) вызванные потенциалы. В полученных группах возможна классификация по половому признаку, возрасту. При патологиях также необходима классификация, но её провести намного сложнее, чем для нормы. Это является следствием того, что при патологии очень большая вариабельность формы колебаний ВП. В результате классификации всё множество реализаций будет разделено на подмножества, каждую из которых в дальнейшем будем называть вероятностной компонентой, принадлежащей к гауссовскому параметрическому семейству распределений. В этом случае можно записать полигауссовую многомерную плотность вероятности вектора дискретных значений напряжения ВП:
,
,
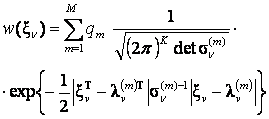где
- вектор измерения, 
- вектор математического ожидания, 
- ковариационная матрица, 
- вероятность появления компоненты с номером 
, 
- размерность вектора измерения.
Адекватное описание реализаций ВП можно представить в виде односвязного марковского процесса. В этом случае векторная модель будет определяться двумя уравнениями: уравнением сообщения и уравнением наблюдения, имеющие следующий вид:
,
,
,
,
где 
, 
,
, 
- номер отсчёта, 
- номер вероятностной компоненты, 
- вектор значений математического ожидания реализаций, 
- вектор отсчётов значений смещения математического ожидания между компонентами, 
- матрица коэффициентов, связывающих отсчёты на текущем шаге с отсчётами на предыдущем шаге размерностью (К ´ К) (К - количество каналов измерения), 
- вектор независимого векторного белого гауссовского шума с нулевым математическим ожиданием и корреляционной матрицей 
размерностью (К ´ К), 
- вектор независимого векторного белого гауссовского шума с нулевым математическим ожиданием и корреляционной матрицей 
размерность (К ´ К). Обозначим 
вероятность появления реализации, принадлежащей к той или иной компоненте под номером
. Тогда по условию нормировки 
. Диагональные элементы матрицы 
характеризуют величину влияния предыдущего отсчёта реализации на текущий отсчёт одного канала, а недиагональные - влияние предыдущего отсчёта на текущий отсчёт между разными каналами.
Для синтеза алгоритма выделения низкоамплитудных биопотенциалов на основе модели в виде вероятностной смеси воспользуемся теорией проверки статистических гипотез. При этом в выражении для условной плотности вероятности при выдвижении гипотезы о том, что на входе присутствует компонента с номером m , будет участвовать неизвестные истинные значения сообщения 
. Согласно литературе вместо неизвестных истинных значений сообщения используются их оценки. Их можно получить с помощью фильтров Калмана, настроенных на соответствующие компоненты. Тогда выражение для условной плотности вероятности будет иметь вид:
,
где 
- вектор оценки фильтра, настроенного на m компоненту, 
- ковариационная матрица вектора измерения, ковариационная матрица, определяющаяся по формуле: 
. 
- ковариационная матрица оценки фильтра.
Построив отношение правдоподобия и взяв его логарифм получим следующее выражение:
,
где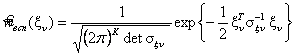 
- вспомогательная плотность распределения. Тогда правилом выбора гипотезы будет следующим:
, 
,
где 
- номер фильтра, настроенного на m-ую компоненту.
Структурная схема полигауссова алгоритма представлена на рис. 1.
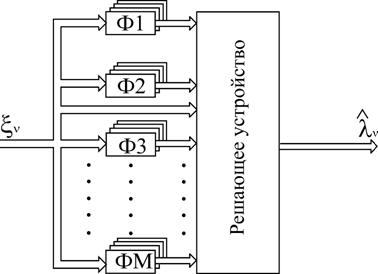
Рисунок 1.
Ф1 - ФМ - фильтры, настроенные каждый на свою компоненту. В решающем устройстве производится вычисление логарифмов отношений правдоподобия и принятие решения в соответствии с правилом выбора гипотез.
При анализе разработанного алгоритма выделения ВП было установлено уменьшение ошибки обработки в 1,3 раза по сравнению с алгоритмом, где используется один фильтр Калмана, моделью для которого является реализация ВП, являющаяся результатом усреднения по всем вероятностным компонентам. Решающее устройство в 75,2% случаях приняло правильные решения.