Современные наукоемкие технические процессы невозможно реализовать без дополнения их современными достижениями теории управления. Как известно, во многих линейных управляемых системах, управляющие параметры могут находиться как в правой части уравнения, так и в граничных условиях. Кроме того, многие важные в теории управления множества обладают свойствами инвариантности. Также известны необходимые и достаточные условия слабой инвариантности области выживания при различных ограничениях на управления [1, 4, 6].
Известно, что задача приведения фазовой точки на целевое множество G с дальнейшим удержанием на нем эквивалентна задаче приведения фазовой точки на ядро живучести области выживания G. При этом возникает следующий вопрос качественного характера, который рассматривается в данной работе: существует ли непустое подмножество множества G, слабо инвариантное относительно рассматриваемой управляемой системы [2].
Постановка задачи. Пусть дана линейная управляемая система
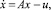(1)
где x ∈ R – фазовый вектор, A – d×d матрица, u ∈ P – параметр управления, который принимает значения из непустого выпуклого компактного подмножества пространства Rd.
Определение 1. Множество Y ⊂ Rd называется слабо инвариантным относительно системы (1), если для любой начальной точки x0 ∈ Y существует управление такое, что для всех t ≥ 0.
Определение 2. Множество Y ⊂ Rd называется сильно инвариантным относительно системы (1), если для любых x0 ∈ Y и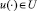 
, существует 
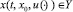при всех t ≥ 0.
Определение 3. Максимальное подмножество Y ⊂ Rd, слабо инвариантное относительно системы (1), называется ядром живучести множества Y относительно системы (1) и обозначается через core(1)Y.
Предположим, что G – непустое выпуклое замкнутое подмножество Rd. Ядро выпуклого множества G, которое обозначим через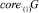 
, является выпуклым замкнутым подмножеством G [3].
Вектор a ∈ Rd называется асимптотическим направлением множества Y ⊂ Rd, если Y + λa ⊂ Y для всех λ ≥ 0. Совокупность всех асимптотических направлений множества Y обозначим через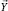 
, т.е.
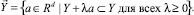
Согласно определению ядро множества Y ⊂ Rdотносительно однородной системы
(2)
определяется формулой
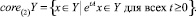
Положим
L = A–1P,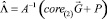 
,
где A–1Z – прообраз множества Z при отображении A.
Результаты. Лемма 1. Справедливы включения
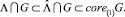
Доказательство. Первое включение вытекает из определений множеств L, 
, так как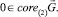 
Пусть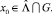 
По определению множества 
найдется u0 ∈ P такое, что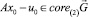 
и x0 ∈ G. Положив u(t) ≡ u0, рассмотрим соответствующую траекторию системы (1). Поскольку 
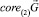сильно инвариантно относительно системы (2), то
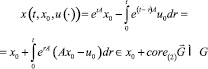
при всех t ≥ 0. Следовательно,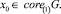 
Лемма доказана.
Согласно лемме [8], если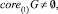 
то
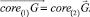(3)
Отсюда следует, core(1)G компактно, если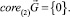 
Также из теоремы [7] получим 
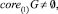если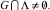 
Лемма 2. Пусть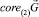 
не является линейным подпространством Rd. Тогда существует собственный вектор матрицы A, принадлежащий 
.
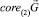Доказательство. На единичной сфере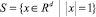 
рассмотрим систему
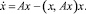(4)
Ясно, что если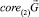 
есть луч, то его направляющий вектор будет собственным для матрицы A. Далее, пусть 
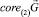отлично от луча. Положим 
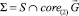. Так как выпуклый конус 
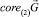не является линейным подпространством Rd, то найдется ненулевой вектор m ∈ Rd такой, что (m, y) ≥ 0 для всех y ∈ Σ. Отсюда следует, что оператор ортогонального проектирования Π из Rd на 
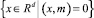является гомеоморфизмом Σ на ΠΣ. Ясно, что ΠΣ есть выпуклый компакт. Поэтому Σ обладает свойством неподвижной точки [5]. Пусть xtодна из неподвижных точек. В силу компактности Σ существует последовательность {tn} такая, что tn ↓ 0 и 
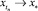, x* ∈ Σ при n → +∞ Далее, аналогично теореме [7] доказывается, что x* – точка покоя системы (4), т.е. 
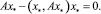Таким образом, единичный вектор 
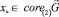является собственным для матрицы A. Лемма доказана.
Из доказанной леммы следует, если матрица A не имеет действительных собственных чисел, то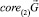 
является линейным подпространством Rd.
Легко убедиться, что если G = G0 + G1 где G0 –линейное подпространство Rd и G1выпуклый компакт, то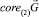 
является максимальным подпространством G0, инвариантным относительно A и 
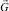= G0.
Теорема 1. Пусть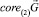 
есть линейное подпространство Rd. Тогда для того, чтобы 
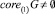необходимо и достаточно, чтобы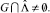 
Доказательство теоремы. Достаточность. Доказательство достаточности теоремы вытекает из леммы 1.
Необходимость. Предположим, что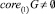 
. Введем обозначения: J – ортогональное дополнение к 
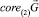в Rd; Π – оператор ортогонального проектирования из Rd на J;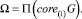 
Из (3) следует, что Ω есть выпуклое компактное подмножество J и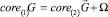 
.
Далее, рассмотрим управляемую систему
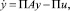(5)
где y ∈ Rd – фазовый вектор, u ∈ P – параметр управления.
Множество Ω является слабо инвариантным относительно системы (5). Действительно, пусть y0 ∈ Ω т.е. y0 = Πx0 для некоторого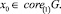 
Согласно определению 3 найдется 
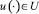такое, что
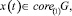(6)
для всех t ≥0 где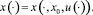 
Так как 
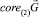инвариантно относительно A, то
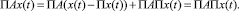(7)
Следовательно, функция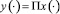 
является решением задачи Коши 
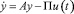, y(0) = y0. Из (6) следует, что y(t) ∈ Ω для всех t ≥ 0. Таким образом, Ω – слабо инвариантно относительно системы (5).
Далее, по теореме [7] существует точка покоя y* системы (5), принадлежащая Ω. По определению точки покоя найдется u* ∈ P такое, что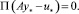 
Следовательно,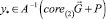 
и включение y* ∈ G очевидно. Теорема доказана.
Теорема 2. Пусть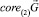 
есть линейное подпространство Rd и detA ≠ 0. Тогда 
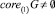в том случае, если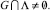 
Доказательство. В соответствии с леммой 1 и теоремой 1 достаточно показать, что если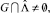 
то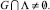 
Предположим, что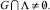 
Поскольку detA ≠ 0 и подпространство 
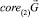инвариантно относительно A, то
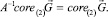
Значит,
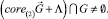(8)
Так как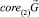 
– линейное подпространство Rd, содержащееся в 
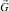, то из (8) вытекает, что 
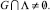Теорема доказана.
Заключение
В статье приведены условия для существования ядра выпуклого множества G, слабо инвариантного относительно линейной управляемой системы. Основными результатами статьи являются:
• Теорема 1. Пусть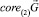 
есть линейное подпространство Rd. Тогда для того, чтобы 
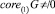, необходимо и достаточно, чтобы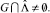 
• Теорема 2. Пусть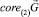 
есть линейное подпространство Rd и detA ≠ 0. Тогда 
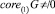в том случае, если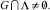 
Рецензенты:
Нысанов Е.А., д.ф.-м.н., профессор кафедры «Теория и методика преподавания информатики» Южно-Казахстанского государственного университета им. М.Ауэзова, г. Шымкент;
Шалданбаев А.Ш., д.ф.-м.н., профессор кафедры «Математические методы и моделирование» Южно-Казахстанского государственного университета им. М.Ауэзова, г. Шымкент.
Работа поступила в редакцию 04.04.2012