Процесс выбора знания из области знаний – это один из важных элементов исследования [3]. Он должен занимать мало времени, быть эффективен, прост и иметь возможность к изменению. Поэтому выбор знания из области знаний нами был исследован как система [5]. Для этого мы использовали системный анализ [2, 5]. В результате был получен метод выбора знания из области знаний для задачи исследования [5], на примере решения которой был проверен этот метод. Чтобы разработать общую методику получения бинарного дерева системы вопросов и ответов для любой области знаний, нам потребовалось выявить общие положения при получении корня, промежуточных узлов и листьев бинарного дерева по имеющейся классификации представленных знаний. Сначала были составлены правила получения корня бинарного дерева системы вопросов и ответов. Они помогли выбрать критерии, заложенные в вопросы, и в процессе решения будут отсекать неподходящие знания из заданной области знаний. Теперь мы сможем произвести исследование бинарного дерева системы вопросов и ответов [4] и разработать правила получения промежуточных узлов дерева, его листьев и способ формирования дерева.
Цель исследования – формулировка правил для получения элементов бинарного дерева системы вопросов и ответов и способа его формирования, чтобы разработать методику получения дерева системы вопросов и ответов для любой области знаний.
Материал и методы исследования
С развитием научно технического прогресса (НТП) [6] решаемые задачи усложняются, так как появляются всё новые знания об объектах исследования. Если сначала определённый объект исследования характеризовало определённое основное свойство, то после появления нового объёма знаний об этом объекте исследования, оно изменит свои параметры и перестанет быть основным.
Свойство с параметром A или свойство n разбивают новый объём знаний З2 на две части З1 и DЗ (рис. 1,а)). Это разбиение выразится в бинарном дереве системы вопросов и ответов определённым образом (см. рис. 1,б)). Здесь свойство с параметром A или свойство n, было представлено нами в виде вопроса, что помогло получить корень дерева, разбивающий область знания на две части – З1 и DЗ (см. рис. 1,б)).
а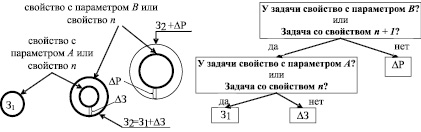 б
б
Рис. 1. Получение нового корня бинарного дерева системы вопросов и ответов: а – разбиение области знания З2 + DР на две части З2=З1 + DЗ и DР свойством с параметром B или свойством n + 1; б – получение нового корня дерева, разбивающего область знания З2 + DР на две части З2=З1 + DЗ и DР; З2 – предыдущая новая область знаний, применимых к изменённому под воздействием НТП объекту исследования, который имел основное свойство с параметром B или основное свойство n + 1, перед новым изменением объекта исследования; DР – это новый объём знаний из области знаний, соответствующий объекту исследования, для решения появившегося нового объёма научных задач после нового изменения объекта исследования
Если под воздействием НТП опять изменится объект исследования, то появится новый объём знаний DР с новым основным свойством с параметром C или новое основное свойство n + 2. Новая область знаний, применимых к изменённому под воздействием НТП объекту исследования, который имел до этого изменения основное свойство с параметром B или основное свойство n + 1, будет равна З2 + DР = З1 + DЗ + DР. Тогда получим новый корень бинарного дерева (см. рис. 1,б)), разбив область знания З2 + DР на две части З2 = З1 + DЗ и DР свойством с параметром B или свойством n + 1 (см. рис. 1,а)). Бывшее до нового изменения основное свойство с параметром B или основное свойство n + 1 будет корнем дерева.
Произведя аналогию и для следующего изменения объекта исследования, были сформулированы правила получения корня бинарного дерева системы вопросов и ответов.
Правило 1. Если под воздействием НТП объект исследования изменил своё свойство с параметра A на параметр B, то корнем бинарного дерева системы вопросов и ответов станет вопрос: «У задачи свойство с параметром A?».
Правило 2. Если под воздействием НТП объект исследования изменил своё свойство с n на n + 1, то корнем бинарного дерева системы вопросов и ответов станет вопрос: «Задача со свойством n?».
Исследуем бинарное дерево выбора метода оптимизации из известного объёма методов (см. рис. 2) [1, 5]. Из рисунка видно, что указанные вопросы соответствуют определённым базовым свойствам математической модели, описывающей оптимизационную задачу. Вопрос: «В функции минимизации одна переменная?» характеризует задачи оптимизации с общим свойством – «задача оптимизации формулируется функцией минимизации с одной переменной». Это будет свойство с параметром A = 1. Тогда вопрос: «Область, в которой происходит задача оптимизации – это конечномерные пространства?» отделяет две области знаний – это методы оптимизации, где ограничения формируют конечномерные пространства (со свойством n), и методы, формирующие функциональные пространства. А последний вопрос: «В задаче одна целевая функция?», отделяет методы свойством c параметром B = 1, где число целевых функций в задаче оптимизации равно 1. Данные свойства A, n и B ретроспективно отражают исторический ход появления новых групп методов (рис. 3) под воздействием НТП, так как необходимо решать более сложные задачи оптимизации. Чтобы получить данные свойства, которые станут узлами бинарного дерева системы вопросов и ответов, нами была использована соответствующая литература об исследуемой области знаний [1], в которой отражена классификация знаний, применимых к заданному объекту исследования, представленная в хронологическом порядке появления.
До момента времени t1 (см. рис. 3) все методы (объём знаний З1) имели свойство с параметром A = 1. Далее в период с t1 до t2 методы (добавочный объём знаний ∆З) имели свойство n. А с t2 до t3 новые методы (объём знаний ∆Р) будут иметь свойство с параметром B = 1. А после t3 методы (объём знаний ∆Л) имеют свойство c параметром B > 1. Так методы были разделены на группы, объединённые определённым свойством.
Разделены методы в пределах этих объёмов знаний (З1, ∆З, ∆Р и ∆Л). Из рис. 2 видно, что ∆З, ∆Р и ∆Л – это системы вопросов I, III и IV, которые разбивают каждую область знаний на группы методов объединённых определённым свойством (n, с параметром B = 1 и c параметром B > 1). З1 объединяет одну группу методов свойством c параметром A = 1. Поэтому система вопросов II ( см. рис. 2) должна распределить методы внутри одной группы.
Каждый метод оптимизации разрабатывается под решение задачи с определёнными свойствами. Поэтому необходимо выявить исторический ход появления каждого метода из данной группы, как реакцию на появление более сложных задач оптимизации под воздействием НТП. Другими словами, ищется свойство, отделяющее более сложный метод из данной группы методов. Из оставшихся методов определяется и отделяется ещё один метод и так далее. Этот процесс напоминает рис. 3, только вместо З1, ∆З, ∆Р и ∆Л будут листы дерева – методы из данной группы З1 (рис. 4).
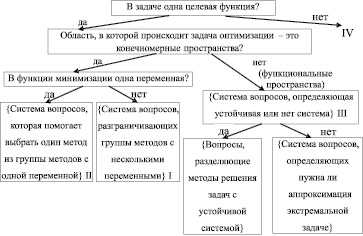
Рис. 2. Примерная схема выбора метода оптимизации для решения исследуемой задачи
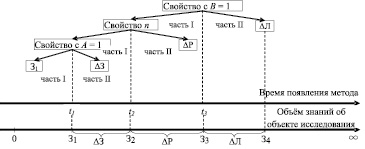
Рис. 3. Исторический ход появления новых групп методов, под воздействием НТП, в результате необходимости решения более сложных задач оптимизации
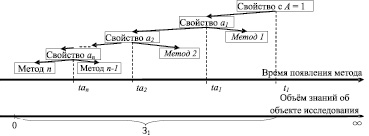
Рис.4. Определение ряда свойств a1, a2, …, an, разбивающих группу методов со свойством c параметром A = 1 на методы от более сложного метода к простому
Объём знаний ∆З объединяет в себе несколько групп методов, поэтому выявим свойства отделяющие каждую из таких групп методов по принципу их временного появления под воздействием НТП (рис. 5). Разобьём каждую группу на методы, как для области знаний З1 (см. рис. 4). Аналогичным образом поступим с объёмами знаний ∆Р и ∆Л.
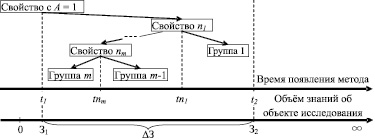
Рис. 5. Определение ряда свойств n1, …, nm, разбивающих ∆З на m групп методов – Группа 1, …, Группа m-1 и Группа m по принципу их временного появления под воздействием НТП
Результаты исследования и их обсуждение
Используя Правила 1 или 2, вся область знаний будет разбита корнем дерева (свойством с параметром B = 1) на две части. Далее необходимо применить эти Правила к первой части знаний, как к общей области знаний, выявив ещё один корень поддерева (свойство n), разделив первую часть знаний на две части. Будем применять разделение первой части знаний до тех пор, пока свойство не отделит такую первую часть, в которой будет расположена одна группа методов, объединённых этим свойством. Корень бинарного дерева системы вопросов и ответов, а также корни поддеревьев сформируют вырожденное левостороннее бинарное дерево системы вопросов и ответов. Основное свойство станет корнем дерева, а остальные – промежуточными узлами. То же применим для вторых частей дерева и поддеревьев, пока во вторых частях поддеревьев не останется по одной группе знаний. Получаемые корни поддеревьев становятся промежуточными узлами. Тогда сформулируем правило получения промежуточных узлов.
Правило 3. Необходимо использовать Правило 1 или Правило 2, разбивая каждую область знания на две части до тех пор, пока во всех частях не останется по одной группе знаний, объединённых одним общим свойством. Здесь выявленный корень для каждой части будет промежуточным узлом бинарного дерева системы вопросов и ответов, кроме одного корня дерева с основным свойством первой части всей области знаний. Он является корнем бинарного дерева системы вопросов и ответов.
Чтобы получить оставшиеся промежуточные узлы и листы дерева (знания), разделим все группы знаний, объединённые одним свойством. Для этого составим ещё одно правило.
Правило 4. Необходимо использовать Правило 1 или Правило 2, разбивая каждую группу знаний на две части так, чтобы во второй части оставалось одно знание. Делим первую часть до тех пор, пока во всех частях не получится по одному знанию. Выявленный корень каждой первой части будет промежуточным узлом бинарного дерева системы вопросов и ответов, а разделённые знания листами этого дерева. Знания должны располагаться от более сложного знания к менее сложному знанию вниз по уровням.
Выводы
Исследование бинарного дерева выбора метода оптимизации из известного объёма методов (см. рис. 2–5) позволило сформулировать правила получения промежуточных узлов и листьев бинарного дерева системы вопросов и ответов.
Правило 3. Необходимо использовать Правило 1 или Правило 2, разбивая каждую область знания на две части до тех пор, пока во всех частях не останется по одной группе знаний, объединённых одним общим свойством. Здесь выявленный корень для каждой части будет промежуточным узлом бинарного дерева системы вопросов и ответов, кроме одного корня дерева с основным свойством первой части всей области знаний. Он является корнем бинарного дерева системы вопросов и ответов.
Правило 4. Необходимо использовать Правило 1 или Правило 2, разбивая каждую группу знаний на две части так, чтобы во второй части оставалось одно знание. Делим первую часть до тех пор, пока во всех частях не получится по одному знанию. Выявленный корень каждой первой части будет промежуточным узлом бинарного дерева системы вопросов и ответов, а разделённые знания – листами этого дерева. Знания должны располагаться от более сложного знания к менее сложному знанию вниз по уровням.
Рецензенты:
Максименко Л.А., д.т.н., профессор кафедры вычислительной техники и АСУ, ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар;
Лойко В.И., д.т.н., профессор, заведующий кафедрой компьютерных технологий и систем, ФГБОУ ВПО «Кубанский государственный аграрный университет», г. Краснодар.
Работа поступила в редакцию 04.04.2012.



