1. Конструкция ортопедического аппарата автоматизированного остеосинтеза
Ортопедический аппарат автоматизированного остеосинтеза (далее – аппарат) с тремя независимыми прецизионными электромеханическими приводами (ЭМП) разработан в ВлГУ [1] взамен компрессионно-дистракционного аппарата с ручным приводом проф. Г.А. Илизарова.
Как и в аппарате с ручным приводом в нем используются кольца со спицами, фиксируемыми на соединяемых отломках костной ткани конечности пациента (рис. 1), но раздвигаются кольца в процессе лечения управляемыми ЭМП линейного перемещения на базе шаговых микроэлектродвигателей (ШД) и планетарных роликовинтовых передач (ПРВП). Шарнирно-стержневая система аппарата (ШСС) совместно с ЭМП обеспечивает циклические продольные и угловые смещения подвижного и неподвижного колец. Корпус основного ЭМП жестко фиксируется на неподвижном кольце с возможностью регулирования его углового положения.
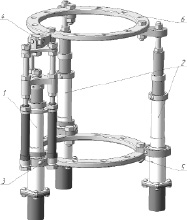
Рис. 1. Ортопедический аппарат автоматизированного остеосинтеза: 1 – основной привод; 2 – дополнительные приводы аппарата; 3 – фиксатор углового положения основного привода; 4 – двухстепенной шарнир; 5,6 – неподвижное и подвижное кольца аппарата
Программное управление ЭМП аппарата осуществляется микропроцессорной системой управления (МПСУ). Параметры цикла дистракции костной ткани: период цикла, величины линейных микроперемещений и скоростей движения для каждого независимого ЭМП задаются с пульта управления. За цикл дистракции время работы ШД составляет 5…7 с, а время остановки около 40 мин. Самотормозящиеся ПРВП в составе ЭМП фиксируют относительное положение колец во время остановки ШД, что существенно экономит энергию питающего аккумулятора.
2. Результаты испытаний и модернизация аппарата
Разработанный аппарат реализует широкий круг ортопедических задач. Вместе с тем недостатки, выявленные в процессе испытаний, потребовали решения ряда задач структурной модернизации сложной мехатронной системы аппарата, направленных на улучшение его главных качественных показателей – массогабаритных, жесткостных и точностных. В этой связи была проведена модернизация всех функциональных частей аппарата – ШСС, ЭМП и МПСУ.
Так, усовершенствованная система измерения и регистрации осевых усилий в составе МПСУ позволила получить точную информацию о фактически развиваемых осевых силах ЭМП [5]. Действительная осевая нагрузка 600 Н оказалась вдвое меньше проектной, что позволило отказаться от планетарных редукторов в ЭМП и заменить их меньшими по массе и габаритам сильфонными муфтами. В результате такой замены сократилась кинематическая цепь и, как следствие, повысились точность, чувствительность и надежность ЭМП.
При практической реализации полученных преимуществ возникла необходимость повышения жесткости исполнительных механизмов ЭМП и ШСС аппарата вцелом. Для этого были разработаны ПРВП с максимально возможным числом резьбовых роликов при сохранении заданного передаточного отношения и самоторможения передачи, а также устройство фиксации углового положения основного ЭМП аппарата [2, 3]. Управляющая программа как составная часть МПСУ также была модернизирована [4].
3. Постановка задачи исследования
Технический уровень аппарата во многом определяют ПРВП, выполняющие в составе трех независимых ЭМП функции исполнительных механизмов. Широкие возможности ПРВП по выбору конструктивных параметров делают актуальной задачу выбора их оптимального сочетания, которое дает наилучшее проектное решение, соответствующее экстремальным значениям доминирующих критериев качества (минимальной массе и максимальной жесткости) механической системы аппарата, при оптимальном цикле дистракции костной ткани. В связи с очевидной противоречивостью названных критериев можно назначить обобщенный относительный критерий – массу, отнесенную к жесткости, который следует минимизировать. Это достаточно простой и эффективный критерий для несущей механической системы аппарата [2].
4. Динамическая модель мехатронной системы аппарата
Для окончательной постановки и решения математической задачи оптимального проектирования необходимо построить динамическую модель сложной мехатронной системы модернизированного аппарата, включающую в себя динамические модели его функциональных частей, с целью всестороннего динамического анализа.
4.1. Математическая модель механической системы аппарата
Так как работа трех независимых ЭМП осуществляется поочередно, т.е. в любой момент времени работает и создает осевое усилие только один из них, то механическую систему аппарата представим в виде трех, шарнирно соединенных между собой стержней (рис. 2). Стержень Г-образной формы схематизирует неподвижное кольцо с закрепленными на нем двумя выключенными в данный момент времени ЭМП. Прямолинейный стержень – подвижное кольцо. Функции третьего стержня (переменной длины) выполняет ПРВП, работающего в данный момент времени ЭМП. Центральный винт ПРВП через упругую муфту связан с ротором ШД, к которому приложен вращающий момент, а выходной шток шарнирно соединен с подвижным кольцом.
Все кинематические пары ШСС аппарата считаем идеальными и голономными. Наиболее податливыми звеньями этой механической системы являются упругая муфта, хрящевая ткань, расположенная между подвижным и неподвижным участками кости, а также связи между этими участками и соответствующими кольцами. Учтем также диссипативные силы внутреннего трения в материале упругих звеньев и потери на трение скольжения и качения в сопряжениях звеньев ПРВП.
В указанной постановке динамическая модель ШСС аппарата представляет собой пятимассовую систему с сосредоточенными параметрами, которая состоит из абсолютно твердых тел, соединенных между собой безынерционными упругодиссипативными элементами, подчинена стационарным, голономным связям и находится под действием потенциальных сил упругости и непотенциальных диссипативных сил.
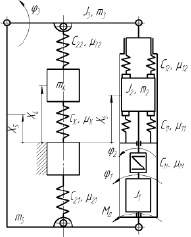
Рис. 2. Динамическая модель механической системы аппарата
Дифференциальные уравнения движения механической системы в общем виде можно записать в форме уравнений Лагранжа в обобщенных координатах
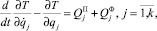
где k – число степеней свободы системы; Т – кинетическая энергия системы; qj – соответствующая обобщенная координата;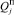 
и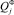 
– обобщенные силы соответственно потенциальных и диссипативных сил.
За обобщенные координаты механической системы примем: φ1 – угол поворота ротора ШД; φ2 – угол поворота блока винта с роликами; φ3 – угол поворота подвижного кольца; x4 – линейная координата подвижного участка кости относительно неподвижного; x5 – линейная координата (деформационная) неподвижного кольца относительно неподвижного участка кости; x6 – линейная координата (деформационная) блока винта с роликами относительно неподвижного участка кости.
Кинетическая энергия механической системы, найденная как сумма кинетических энергий подвижных масс, является квадратичной формой обобщенных скоростей
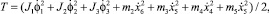
где J1, J2, J3 – моменты инерции, соответственно ротора ШД, блока винта с роликами и подвижного кольца, приведенные к оси винта; m2 – масса блока винта с роликами; m3 – масса подвижного кольца; m4 – масса подвижного участка кости, мышц и кожи; m5 – суммарная масса неподвижного кольца и связанных с ним корпусных деталей ЭМП.
Обобщенные силы для потенциальных сил упругости, соответствующих каждой из обобщенных координат, вычислим по формуле
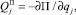
запишем потенциальную энергию системы как функцию обобщенных координат
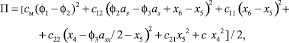
где см – крутильная жесткость сильфонной муфты; с11 и с12 – линейные жесткости в сопряжениях роликов с опорной и ходовой гайкой соответственно; с21 и с22 – линейные жесткости связи колец соответственно с неподвижным и подвижным участками кости; сх – линейная жесткость хрящевой ткани; as = S/2π; S – перемещение ходовой гайки за оборот винта.
Обобщенные силы диссипативных сил найдем как коэффициенты в сумме возможных работ диссипативных сил, соответствующих положительным приращениям обобщенных координат δqj
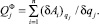
Тогда
где МД – момент ШД; μм – коэффициент демпфирования в сильфонной муфте.
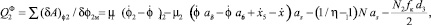
где μ12 – коэффициент демпфирования в сопряжениях роликов с ходовой гайкой; η – КПД прямого хода ПРВП; N1 = с12(φ2as – φ3as + x4 – x5) – осевая сила в резьбовом сопряжении опорной гайки с роликами; N2 = с11(x6 – x5) – осевая сила в резьбовом сопряжении ходовой гайки с роликами; fk – приведенный коэффициент трения качения; d3 – средний диаметр резьбы гайки.
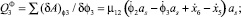
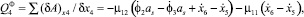
где μ11 – коэффициент демпфирования в сопряжении роликов с опорной гайкой.
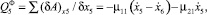
где μ21 – коэффициент демпфирования связи кольца с неподвижным участком кости.
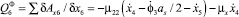
где μ22 – коэффициент демпфирования связи кольца с подвижным участком кости; μx – коэффициент демпфирования хрящевой ткани.
После соответствующих преобразований получим математическую модель механической части аппарата в виде системы линейных дифференциальных уравнений с постоянными коэффициентами
4.2. Математическая модель шагового электродвигателя
Зависимость МД от параметров движения зададим динамической характеристикой шагового электродвигателя, определяющей характер его взаимодействия с механической системой аппарата и МПСУ. С учетом дифференциального уравнения вращения ротора ШД [6] выражение для МД можно представить в виде:
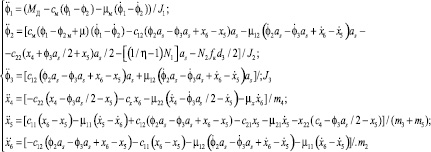
где μД – коэффициент вязкого трения ШД; N – число витков в обмотке статора; Фм – максимальный магнитный поток; р – число пар магнитных полюсов ротора двигателя; λ – угол между обмотками ШД; I1, I2 – токи, поступающие на обмотки статора ШД с МПСУ.
Токи в обмотках статора находятся из дифференциальных уравнений:
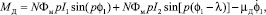
где U – напряжение источника питания электродвигателя; L – собственная индуктивность каждой фазы; R – сопротивление цепи обмотки статора.
4.3. Математическая модель микропроцессорной системы управления
Управление работой ШД происходит путем чередования управляющих импульсов прямоугольной формы, формируемых МПСУ в соответствии с заданной программой. Эти импульсы преобразуются в импульсы напряжения и поступают на обмотки статора двигателя. Полагая МПСУ дифференцирующим звеном с замедлением с постоянной времени Тэл и коэффициентом усиления сигнала Ку, запишем дифференциальные уравнения изменения напряжений на обмотках статора в виде:
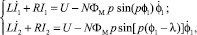
Эти уравнения представляют собой математическую модель МПСУ.
5. Направления дальнейших исследований
Таким образом, на основе построенных динамических моделей функциональных частей модернизированного аппарата сформирована математическая модель мехатронной системы аппарата в целом. Динамический анализ аппарата сводится к нахождению периодических решений системы дифференциальных уравнений математической модели при различных значениях массогабаритных и упругодиссипативных параметров для оценки их влияния на основные показатели качества аппарата. В связи с математическими трудностями, обусловленными нелинейностью и высоким порядком системы, эту задачу целесообразно решать численными методами на ЭВМ.
По результатам динамического анализа можно обоснованно задать значения фиксированных конструктивных параметров и назначить диапазоны изменения варьируемых параметров, что позволит сформировать задачу оптимального проектирования в окончательном виде.
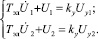
Рецензенты:
Кульчицкий А.Р., д.т.н., профессор, заместитель главного конструктора по испытаниям ООО «ВМТЗ», г. Владимир;
Гоц А.Н., д.т.н., профессор кафедры тепловых двигателей и энергетических установок ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
Работа поступила в редакцию 04.04.2012.