Интенсивная информатизация общества создала необходимость в увеличении методического обеспечения для продуктивной учебной деятельности учащихся общеобразовательных учреждений. На первый план в обучении выдвигается формирование исследовательских умений: анализировать информацию, систематизировать ее, сравнивать, отделять главное от второстепенного, обобщать, выдвигать предположения о возможных путях решения проблемы, приводить примеры и контрпримеры и т.п.
Роль математики как важнейшего инструмента в развитии исследовательских форм мышления школьника бесспорна, но ее содержание и традиционные методики требуют значительного увеличения доли исследовательских задач и методов даже в раскрытии общеизвестных школьных тем. Эта проблема обусловлена, с одной стороны, человеческим фактором – качеством и содержанием профессиональной подготовки учителей, их настроением, современной системой воспитания детей, с другой стороны, неразработанностью общеизвестных, качественных и доступных методик обучения решению задач, развивающих у учащихся общеобразовательных учреждений продуктивный уровень усвоения учебного материала.
В современной теории обучения математике одним из приемов развития эвристического и творческого типа продуктивных действий учащегося является решение задачи с параметром. Задача с параметром, по мнению П.М. Эрдниева, – это естественный этап в решении любой математической задачи [6]. Отсюда актуальность этой проблемы обусловлена не столько потребностями ГИА и ЕГЭ, сколько необходимостью создания целостной методики обучения, включающей обеспечение развития у школьников продуктивного уровня усвоения учебного материала по многим темам, в частности, по решению уравнений и неравенств.
В требованиях к уровню подготовки выпускников основной школы написано, что «в результате изучения математики ученик должен уметь решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы; решать линейные, квадратные неравенства с одной переменной и их системы» [4, c. 21]. Ни в энциклопедии элементарной математики, ни государственном образовательном стандарте нет понятия «уравнение (неравенство) с параметром», не представлены методы их решения. Поскольку параметризировать можно любую математическую задачу, получаем, что все уравнения и неравенства делятся на две группы – без параметров и с параметрами. Поэтому существующий в школьной методике математики подход – ставить уравнения (неравенства) с параметрами в один ряд с квадратными, дробными, логарифмическими, содержащими модуль и др. – не имеет под собой никакого обоснования. Исходя из сущности задач с параметрами, их решение – это качественное обобщение и систематизация учебного опыта учащегося на более высоком продуктивном уровне деятельности. Поэтому технология решения задач с параметрами должна быть гармонично вплетена в каждую тему, четко оговорена, должны быть разобраны примеры, приведена система упражнений.
У школьников понятие уравнения (неравенства) с параметром должно включать в себя понимание того, что:
1. Уравнение (неравенство) с параметром – это семейство уравнений (неравенств) одного вида при одних значениях параметра, других видов – при других значениях параметра, при каких-то значениях параметра в это семейство входят верные или неверные тождества (числовые неравенства). Так, уравнение
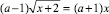
при а = 1 принимает вид линейного; при а = ‒1 становится простейшим иррациональным; если а ≠ 1, а ≠ −1, – уравнение иррациональное.
2. Решение уравнения (неравенства) может включать в себя несколько методов решения, соответствующих каждому виду уравнения при определенных значениях параметра. Например, при каком-то значении параметра неравенство линейное, поэтому решаем его аналитически тождественными преобразованиями; при остальных значениях параметра неравенство квадратичное, – решаем его функционально-графическим способом.
Выделим в обучении решению уравнений (неравенств) пять уровней подготовки учащихся по теме «Уравнения и неравенства»:
1) умение решать простейшие уравнения (неравенства);
2) умение решать уравнения (неравенства), приведенные к простейшим, путем «несложных» тождественных преобразований (прибавление числа к обеим частям уравнения (неравенства), деление обеих частей уравнения (неравенства) на число, приведение к общему числовому знаменателю, приведение подобных и т.п.);
3) умение решать простейшие уравнения (неравенства) с параметрами и уравнения (неравенства), приводимые к ним путем «несложных» тождественных преобразований;
4) умение решать уравнения (неравенства), приведенные к простейшим, путем «сложных» преобразований (использование формул сокращенного умножения, замены переменой, разложения на множители, свойств функций и ее графика и др.);
5) умение решать уравнения (неравенства) с параметрами, приведенные к простейшим, путем «сложных» преобразований.
Уровни 1-й и 2-й обеспечивают репродуктивную деятельность школьника, 3-й и 4-й – как репродуктивную, так и продуктивную, 5-й уровень обеспечивает продуктивную деятельность школьника при решении уравнений и неравенств. При обучении должна соблюдаться преемственность развития вышеперечисленных уровней. Так, выпускники 8-го класса в процессе обучения должны уметь решать следующие уравнения в соответствии с уровнями подготовки:
1) х2 ‒ 2х + 3 = 0;
2) 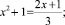
3) х2 + 2х + ах ‒ 3 = 0;
4) (х + 2)4 ‒ 3 = 2х2 + 4х;
5) (х + а)4 ‒ 4(х + а)2 = х2.
Значит, существует потребность методического обеспечения решения уравнений (неравенств) с параметрами на двух уровнях (3 и 5). Уровень 3 – это методика решения простейших уравнений (неравенств) с параметризацией различных числовых коэффициентов (табл. 1), и уровень 5 – более сложных уравнений (неравенств), решаемых аналитическим, функционально-графическим или геометрическим методами. Но простейшие уравнения (неравенства) с параметризацией различных коэффициентов не одинаковы по степени сложности. В табл. 1 более простая параметризация обозначена уровнем (3.1), более сложная – (3.2).
Таблица 1
Различные виды параметризации уравнений и неравенств в 7–9 классах
|
Виды уравнений (неравенств) с параметрами |
Параметризация |
Уровни |
Примеры |
|
|
1. |
Линейные уравнения (неравенства) |
– свободного члена; |
3.1 |
2х = а ‒ 4 |
|
– коэффициента при переменной; |
3.1 |
(а ‒ 2)х < 4 |
||
|
– свободного члена и коэффициента при переменной |
3.2 |
(а ‒ 2)х ≤ 4а |
||
|
2. |
Рациональные уравнения с двучленами первой степени в числителе и знаменателе |
– свободного члена в числителе; |
3.1 |
|
|
– свободного члена в знаменателе; |
3.1 |
|
||
|
– свободных членов в числителе и в знаменателе; |
3.2 |
|
||
|
– коэффициентов при переменной в числителе или знаменателе. |
3.2 |
|
||
|
3. |
Квадратные уравнения (неравенства) |
– свободного члена; |
3.1 |
х2 ‒ 2х + а + 3 ≥ 0 |
|
– коэффициента при переменной 1-й степени; |
3.1 |
х2 ‒ (2 + а)х + 3 = 0 |
||
|
– коэффициента при старшем члене; |
3.2 |
ах2 ‒ 2х + 3 ≤ 0 |
||
|
– коэффициентов при переменной или свободном члене. |
3.2 |
ах2 ‒ (2 + а)х + 3 = 0 |
||
|
4. |
Иррациональные уравнения |
– под знаком квадратного радикала; |
3.1 |
|
|
– вне знака квадратного радикала; |
3.1 |
|
||
|
– под знаком радикала и вне знака радикала |
3.2 |
|
При первом ознакомлении учащихся с простейшими уравнениями (неравенствами) с параметрами учителю необходимо показать единство и взаимосвязь между уравнениями (неравенствами) без параметра с уравнениями (неравенствами) с параметром. Для решения этой задачи можно использовать решения частных случаев уравнений (неравенств) с параметрами [5]. В различных учебных пособиях, в частности, направленных на повышение качества подготовки учащихся по решению задач с параметрами, решения в частных случаях не представлены. Но многолетняя практика обучения решению задач с параметрами показала, что решение частных случаев задач с параметром – это необходимый «мост», связывающий в единое целое задачи с параметром и без параметра. Решения в частных случаях способствуют развитию следующих видов продуктивной учебной деятельности учащихся: умение выделять частные случаи, анализ общих свойств и умение находить отличия в решениях и ответах, умение выдвигать гипотезу о методе решения задачи и доказывать ее состоятельность или опровергать ее. Для педагога использование частных случаев при изучении уравнений и неравенств – это инструмент для качественной актуализации уравнений (неравенств) без параметров, возможность успешно вводить уравнения (неравенства) с параметрами на раннем этапе обучения (в 7 классе) и качественно систематизировать и обобщать изученный материал в средней и старшей школе. Решение частных случаев желательно размещать в сравнительную таблицу (табл. 2), которая должна показывать единство этапов решений частных случаев и подводить к решению задачи с параметром.
Задача. Решите уравнение 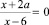 с параметром а.
с параметром а.
Вопрос: «Какие корни будет иметь уравнение при а = 2, а = 0, а = ‒3?» Составим сравнительную табл. 2:
Таблица 2
Представление частных случаев и решения уравнения с параметром на начальных этапах обучения
|
Частные случаи |
Решение уравнения |
||||
|
Если |
а = 2 |
а = 0 |
а = – 3 |
2а = –6, т.е. а = –3 |
2а ≠ –6, т.е. а ≠ –3 |
|
то |
|
|
|
|
|
|
Тогда |
х + 4 = 0 |
х = 0 |
нет корней |
нет корней |
х + 2а = 0 |
|
Ответ: |
х = ‒4 |
х = 0 |
нет корней |
нет корней |
х = ‒ 2а |
Частные случаи подобраны так, что представлены различные исходы: при а = 2 и а = 0 уравнение принимает вид дробного; при а = ‒3 обращается в неверное равенство. В этом случае учитель может обобщить: уравнение с параметром будет дробным, если числитель не равен знаменателю; иначе получим неверное числовое равенство. Табличное представление частных случаев позволяет увидеть методы решения уравнения с параметром (табл. 2). После решения задачи учитель может сформулировать следующие вопросы: при каких значениях параметра данное уравнение имеет единственный корень; не имеет корней? При каком значении параметра корень уравнения равен 9? Как можно выразить параметр а через переменную х? Опишите методику решения дробных уравнений вида 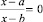 .
.
После решения уравнения необходимо правильно записать ответ.
Ответ: если a = ‒3, то корней нет; если a ∈ (–∞; ‒3) ∪ (‒3; +∞), то х = ‒2а.
Используя ответы в частных случаях, можно провести частичную проверку ответа. Подставим а = 2 и а = 0 в ответ решения: при a = 2 получим х = ‒2а = ‒4; при a = 0 получим х = ‒2а = 0, – те же ответы получены при решении частных случаев.
Так можно решать простейшие уравнения и неравенства с параметризацией различных числовых коэффициентов уровня 3.1.
В формировании понятия уравнения и неравенства с параметром важным является форма учебных заданий, их количество и место в учебном пособии. Анализ задач на решение уравнений и неравенств с параметрами, предлагаемых авторами самых популярных учебных пособий для общеобразовательных учреждений в нашей стране, показывает, что с 7-го класса по 9-й представлено: у Г.В. Дорофеева, С.Б. Суворовой, Е.А. Бунимовича и др. – 27 задач; А.Г. Мордковича, Е.Е. Тульчинской, Т.Н. Мишустиной – 46 задач; С.М. Никольского, М.К. Потапова, Н.Н. Решетникова, А.В. Шевкина – 34; Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова и др. – 31 задача; Ю.Н. Макарычева, Миндюка Н.Г., Муравина К.С. и др. – 17 [1, 2, 3 и др.]. В подавляющем большинстве уравнения и неравенства с параметрами представлены в категории задач повышенной сложности, что изначально ставит психологический барьер в решении задач с параметрами перед большинством учащихся, и примерно половина задач в разделах повторения по главе. Из всех видов задач с параметрами лучше всего представлены задачи на нахождение значений параметра, при которых корни уравнения (неравенство) обладают заданными свойствами. Например, «Корни х1 и х2 уравнения х2 + 6х + а = 0 удовлетворяют условию х1 = 2х2. Найдите а, х1 и х2». Данный вид задач относится к виду задач, следующих из «ключевой» задачи «Решите уравнение х2 + 6х + q = 0 с параметром а». Без подробного разбора «ключевой» задачи учащийся не способен построить полной картины решения уравнения с параметром, так как получает лишь одну из логических последовательностей, связывающих отдельные свойства изучаемого уравнения. Поэтому существует потребность в создании единого методического комплекса задач, направленного на более качественное усвоение понятия «уравнение (неравенство) с параметром». Методический комплекс задач включает в себя: выбор «ключевой» задачи (задача 3), решение ее частных случаев различными методами (задачи 1 и 2), формулирование задач-следствий и их решение (задачи 4 и 5), формулирование и решение задач с изменением отдельных условий (задача 6).
Комплекс задач на решение задач с параметром по теме«Квадратичные неравенства»
Задача 1. Решите неравенство ах2 + х + а > 0 при следующих значениях параметра а = ‒1, 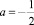 , а = 0,
, а = 0, 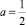 , а = 1. Какой вид принимает неравенство при данных значениях параметра?
, а = 1. Какой вид принимает неравенство при данных значениях параметра?
Комментарий. Задача направлена на закрепление связи понятий «неравенство без параметра» и «неравенство с параметром». Первоочередным при ее решении является развитие у учащихся умений определять вид неравенства при различных значениях параметра и выбор соответствующего метода решения. Так, при а = ‒1 и 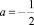 неравенство квадратичное и не имеет решений в действительных числах; при а = 0 – линейное, и в ответе бесконечный числовой промежуток, ограниченный снизу; если
неравенство квадратичное и не имеет решений в действительных числах; при а = 0 – линейное, и в ответе бесконечный числовой промежуток, ограниченный снизу; если 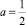 , то неравенство квадратичное, в ответе объединение двух бесконечных промежутков, ограниченных сверху и снизу; если а = 1 – квадратичное, и в ответе интервал.
, то неравенство квадратичное, в ответе объединение двух бесконечных промежутков, ограниченных сверху и снизу; если а = 1 – квадратичное, и в ответе интервал.
Задача 2. Изобразите графики функции f(х) = ах2 + х + а, если а принимает значения ‒3; ‒2; ‒1; 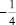 ; 0;
; 0;  ; 1; 2; 3. Покажите на графике положительные значения функции при данных значениях параметра.
; 1; 2; 3. Покажите на графике положительные значения функции при данных значениях параметра.
Комментарий. Цель этой задачи – заложить основы функционально-графических представлений учащихся о выражениях с параметром. Схематично изобразив функцию, необходимо определить отличия и общие свойства графиков при заданных значениях параметра. После показа положительных значений функции необходимо провести сравнительный анализ с условием задачи 1.
Задача 3. Решите неравенство
ах2 + х + а > 0
с параметром а.
Комментарий. Ключевая, системообразующая задача для всех задач комплекса. Решать желательно аналитически, проводя функционально-графические интерпретации, опираясь на решения задач 1 и 2.
Задача 4. При каких значениях параметра а неравенство ах2 + х + а > 0 не имеет корней?
Задача 5. При каких значениях параметра а неравенство ах2 + х + а > 0 имеет решением бесконечный промежуток? интервал?
Комментарий. Решение задач 4 и 5 необходимо вычленить из решения задачи 3 и показать, с одной стороны, что такая формулировка и решение являются частью решения неравенства в целом, с другой стороны, логику решения задач без наличия полного решения неравенства.
Задача 6. Решите неравенство
ах2 + х + а ≥ 0
с параметром а.
Комментарий. Важным вопросом при решении неравенств с параметром является оценка значений корней в зависимости от строгого и нестрогого знака неравенства. Необходимо четко обсудить или даже решить заново неравенство с измененным знаком, провести сравнительный анализ задач 3 и 6.
Представленный методический комплекс обеспечивает подготовку учащихся по решению простейших неравенств с параметризацией двух коэффициентов при неизвестных (уровень 3.2). Подобные комплексы задач также оправдывают себя на начальном этапе решения уравнений (неравенства) с параметрами, приведенных к простейшим, путем «сложных» преобразований (уровень 5).
Изложенные в статье аспекты описывают методическую систему обучения решению уравнений и неравенств с параметрами, апробированную при обучении студентов педагогического отделения по специальности «Математика», школьников старших классов при подготовке к ЕГЭ. Ее эффективность подтверждена высокими результатами обучения: за полугодовой курс школьники и студенты научились определять вид уравнения в зависимости от значений с параметра; 80 % решают простейшие уравнения и неравенства с параметрами; 40 % решают задачи с параметрами, приведенные к простейшим путем «сложных» преобразований. При опросе до изучения темы 98 % учащихся и студентов считали, что они не понимают задач с параметрами и принцип выбора метода решения, не знают методов решения задач с параметром. После изучения курса обучаемые высказали мнение, что в той или иной степени умеют решать уравнения и неравенства с параметрами.
Рецензенты:
Шакирова Л.Р., д.п.н., профессор, Институт математики и механики им. Н.И. Лобачевского Казанского (Приволжского) федерального университета, г. Казань;
Салехова Л.Л., д.п.н., профессор, Институт филологии и искусств Казанского (Приволжского) федерального университета, г. Казань.
Работа поступила в редакцию 12.03.2013.




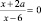
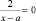
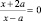
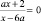

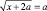
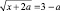
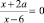
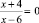 – дробное уравнение
– дробное уравнение
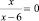 – дробное уравнение.
– дробное уравнение.
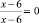 или 1 = 0 – неверное равенство.
или 1 = 0 – неверное равенство.
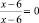 , т.е. 1 = 0 – неверное равенство
, т.е. 1 = 0 – неверное равенство
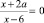 – дробное уравнение
– дробное уравнение