Одним из основных требований, предъявляемых к промышленным регуляторам, является точность реализации закона регулирования и воспроизведения заданного значения регулируемой величины. Это особенно важно в тех случаях, когда на вход регулятора подается непрерывно изменяющийся задающий сигнал. Несмотря на широкое использование ПИД-закона регулирования (по различным данным порядка 90–95 % промышленных регуляторов используют ПИД-закон регулирования [1]), использование этого закона для обеспечения повышенных требований к качеству управления в режиме слежения требует более обоснованного выбора скорости изменения задающего воздействия. Для точного воспроизведения задающего сигнала при выбранном ПИД-законе регулирования необходимо, чтобы скорость изменения сигнала рассогласования ε (t) = g(t) – x(t) (g(t) – задающий сигнал; x(t) – регулируемый сигнал) в переходном процессе не превышала максимального значения скорости перемещения регулирующего органа (РО) исполнительного механизма (ИМ). Очевидно, что скорость изменения ε(t) определяется как скоростью изменения регулируемой переменной x(t), так и скоростью изменения задающего сигнала g(t). Скорость изменения x(t) зависит от инерционности объекта управления, вида, величины и точки приложения возмущения F на объект управления и является независящей от разработчика составляющей сигнала рассогласования. Наименее инерционным и в то же время наиболее тяжелым воздействием, особенно в случае ступенчатого его изменения, является задающее воздействие. Поэтому в реальных автоматических системах регулирования (АСР), скорость изменения задания должна быть ограничена функциональным блоком с временной характеристикой экспоненциальной формы, синхронизируемым с началом воздействия сигнала и со слежением до конечного значения сигнала. Для этого в канал задающего воздействия вводится звено с передаточной функцией
Wg(p) = 1/(Tзp + 1),
в котором постоянная времени Tз ограничивает скорость изменения сигнала задания. Кроме этого, непрерывный входной сигнал контура управления может быть заменен ступенчатым с постоянной величиной шага квантования (дискретизации) Т, который для более точной аппроксимации непрерывного входного сигнала ступенчатым рекомендуется выбирать минимальным [2, 3].
В статье ставится задача: получить математическое соотношение для определения такой постоянной времени Tз, при котором гарантируется воспроизведение задающего воздействия при любом интервале квантования сигнала по времени.
При наличии инерционности и запаздывания в объекте управления и при ограниченной скорости ИМ изменение задающего воздействия g(t) в переходном процессе может опережать сигнал x(t), что окажет влияние на точность воспроизведения сигнала g(t). Поскольку достаточная скорость ИМ не всегда может быть обеспечена в силу технических ограничений, то необходимо, чтобы скорость изменения задающего воздействия g(t) не превышала максимальной скорости изменения x(t). Отсюда следует соотношение для оценки постоянной времени демпфирующего звена Тз, ограничивающего скорость изменения сигнала задания.
Для ограничения скорости изменения сигнала задания достаточно воспользоваться инерционным звеном первого порядка с передаточной функцией
Wg(p) = 1/(Tзp + 1).
Тогда изменение сигнала задания на входе регулятора на единичное ступенчатое воздействие g(t) = 1(t)gо описывается уравнением
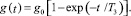 (1)
(1)
В этом случае максимальная скорость изменения сигнала задания g′(t) на интервале времени от 0 до T равна
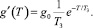 (2)
(2)
Переходный процесс на выходе объекта управления c моделью
Wоб(p) = Коб/(Tоб p + 1)
при действии возмущения F ступенчатого вида описывается уравнением
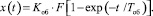 (3)
(3)
При подаче управляющего воздействия максимальной величины Umax = –F переходный процесс на выходе объекта на интервале времени от 0 до Т описывается уравнением
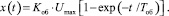 (4)
(4)
Максимальная скорость изменения сигнала x′(t) в этом случае равна
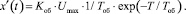 (5)
(5)
Из соотношения g′(t) ≤ x′(t) находим приемлемые значения постоянной времени Тз, при которых скорости изменения g(t) не превышают максимальных значений 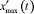 :
:
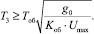 (6)
(6)
На рисунке представлены зависимости максимальной скорости изменения сигнала задания g′(t) от постоянной времени звена Tз при различных интервалах квантования по времени Т. Зависимости получены по формуле (2) для единичного ступенчатого воздействия gо = 1(Т). Как видно из рисунка, максимальная скорость изменения сигнала g(t) при малых значениях постоянной времени Тз существенно уменьшается с увеличением интервала квантования по времени Т. При больших значениях Тз максимальная скорость g′(t) становится малочувствительной к значениям Т. Но с увеличением Т максимальная скорость изменения регулирующего воздействия в переходном процессе μ′(t) уменьшается, а время расчета μ(t) увеличивается, что необходимо учитывать при его выборе, поскольку при достаточной скорости ИМ может происходить снижение быстродействия и уменьшение динамической точности АСР.
При регулировании малоинерционных процессов (например, расхода жидкости, давления, уровня) величина Т может составлять десятые доли секунды [4]. Не рекомендуется выбирать большие периоды квантования для ответственных процессов, так как в этом случае аварийные ситуации будут ликвидироваться слишком медленно. В то же время при слишком малом периоде квантования повышаются требования к быстродействию ЭВМ и увеличивается влияние шумов. Наличие высокочастотных шумовых составляющих в измерительных сигналах приводит к случайным колебаниям исполнительного механизма системы, что в свою очередь снижает точность регулирования. В некоторых случаях шумовые составляющие могут привести к неустойчивому режиму работы системы.
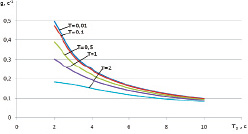
Графики зависимости максимальной скорости изменения сигнала задания g′(t) от постоянной времени звена при различных интервалах квантования по времени Т = 0,01 … 2c
Что касается согласования со скоростью изменения ИМ, то следует заметить, что до сих пор самым распространённым способом регулирования производительности объектов, обеспечивающих транспортировку жидкостей, является использование задвижек или регулирующих клапанов. Но сегодня становится доступным и частотное регулирование асинхронного двигателя. Применение регулируемого электропривода насоса или вентилятора позволяет задать необходимое давление или расход, что обеспечит не только экономию электроэнергии, но и снизит потери транспортируемого вещества. Так, использование частотного регулируемого электропривода обеспечивает значительную экономию электроэнергии: от 30 до 60 % на водонапорной станции и в компрессорных установках, до 75 % в системах вентиляции и кондиционирования [5]. В АСР подобных технологических объектов, например, при регулировании расхода, давления, уровня в системе с частотным электроприводом без транспортного запаздывания, ИМ являются практически безинерционными. При этом устраняются ограничения на необходимую скорость ИМ.
Таким образом, получено соотношение, позволяющее выбрать величину постоянной времени Tз, при котором гарантируется воспроизведение задающего воздействия при любом интервале квантования сигнала по времени. Это позволит наряду с выбором быстродействующего регулятора использовать стандартные ИМ постоянной скорости без заметного снижения качества автоматического регулирования.
Рецензенты:
Червяков Н.И., д.т.н., профессор кафедры «Высшая алгебра и геометрия», ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Ставрополь;
Лубенцов В.Ф., д.т.н., профессор кафедры «Информационные системы, электропривод и автоматика», ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Невинномысск.
Работа поступила в редакцию 25.02.2013.



