На сегодняшний день физические свойства различных покрытий достаточно хорошо известны, это позволяет смоделировать процесс нанесения этих покрытий на основу. Традиционно применяемый для моделирования этих процессов аппарат дифференциальных уравнений не всегда достаточно эффективен. Хорошей альтернативой дифференциальным уравнениям являются модели клеточных автоматов [3, 4]. Теория клеточных автоматов основана на моделировании сложных систем, состоящих из простых объектов, результатом коллективного функционирования которых является сложное поведение всей системы в целом [4, 5]. Модели клеточных автоматов учитывают реальную физико-химическую сущность процесса, позволяют задавать сложные граничные условия, рассматривать фазовые переходы с промежуточными соединениями, выдвигать различные гипотезы относительно формирования фаз и распределения полей концентраций и температур [2, 7].
Данная статья посвящена моделированию процесса нанесения покрытия на гранулы с пористым слоем подложки (например, таблетки).
Описание моделируемого процесса
Процесс формирования оболочек гранул может происходить как в аппарате, представляющем собой вращающийся барабан с горизонтальной осью вращения или колонну псевдоожижения/фонтанирующего слоя.
Подготовленные гранулы загружаются в аппарат, в котором на их поверхность наносится раствор покрытия. Далее гранулы подвергают обкатке для равномерного распределения жидкости. В ходе дальнейшей сушки газообразным сушильным агентом (воздухом) с поверхности гранул начинает интенсивно испаряться влага, концентрация вещества покрытия растет в верхних слоях и, за счет диффузии, распределяется по объему слоя. Через некоторое время в растворе образуется пересыщение и вещество покрытия начинает выкристаллизовываться. Когда скорость испарения влаги с поверхности снизится до определенного уровня, процесс сушки считается завершенным. Процедура нанесения новых слоев раствора с поледующей обкаткой и сушкой повторяют до достижения заданной толщины покрытия.
«Расчетное поле покрытия» формируется путем разбиения поверхности среза гранулы на сетку (рис. 1).
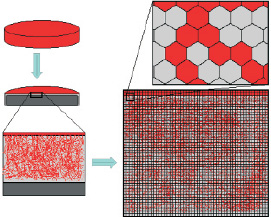
Рис. 1. Формирование расчетного поля:а – вид таблетки; б – сечение таблетки; в – фрагмент среза на поверхности таблетки; г – положение расчетного поля на фрагменте среза; д – фрагмент среза, представленный в виде ячеек клеточного автомата
Клеточный автомат
Для расчета процесса используется двумерный клеточный автомат с квадратной решеткой и окрестностью Мура. По классификации Уоллфрама, автомат относится к автоматам третьего класса [9, 8].
На основании микрофотографий кристаллов на срезе покрытия гранулы был выбран размер клетки, равный 1×1 мкм; общий размер расчетного поля составил 200×400 клеток, шаг по времени, равный 10–3 секунды.
Каждая клетка клеточного автомата может находиться в одном из 4-х фазовых состояний.
Клетка с воздухом (состояние «0») может заполниться жидкостью (состояние «1»), возможен переход «0» → «1».
Клетка с жидкостью может «высохнуть», возможен переход «1» → «0».
Клетка с жидкостью также может «закристаллизоваться», при этом возможен переход «1» → «2» по двум различным механизмам.
Никакие другие переходы невозможны. Клетка с материалом подложки (в состоянии «3») инертна и не может менять своего состояния, а кристалл в рамках модели не может быть растворен (невозможен переход в другое состояние из состояния «2»).
Правила клеточного автомата
При моделировании процесса кристаллизации покрытия необходимо учесть одновременно протекающие процессы: диффузию вещества в растворе, испарение воды с поверхности покрытия и изменение движущей силы испарения вследствие сушки больших объемов гранул, а также учет стерических факторов, влияющих на образование зародыша кристалла и уменьшение толщины покрытия в процессе сушки (усадка). Были сделаны следующие допущения: диффузия происходит по закону Фика; тепловая конвекция не учитывалась; теплота кристаллизации незначительна по сравнению с тепловыми эффектами процесса сушки; глубина пропитки задавалась, исходя из экспериментальных данных о глубине проникновения жидкости в поры подложки, поэтому капиллярные силы не рассчитывались.
Формирование модели пористой подложки
Для начала моделирования процесса требовалось создать такую структуру пор в подложке, в которой все поры сообщались бы с поверхностью. Размеры и количество пор определялись, исходя из экспериментальных данных о структуре подложки.
Был разработан следующий алгоритм: сначала расчетное поле заполняется сплошным слоем вещества подложки на определенную глубину. Затем в верхнем слое случайным образом делаются перфорации, которые будут служить выходами пор. Их количество обусловливает общую пористость слоя. После чего от этих отверстий случайным образом вглубь строятся каналы, которые впоследствии и будут заполняться раствором.
После этого над полем формируется слой раствора; количество клеток в нем определяется, исходя из удельной массы раствора, приходящейся на единицу площади поверхности гранулы.
Правила фазовых переходов
В самом начале цикла над рассчитываемым полем формируется слой раствора необходимого объема, который по специальному алгоритму укладывается на поле и впитывается в поры. В этот момент «воздушные» клетки заполняются влагой и происходит переход «0» → «1».
Далее в процессе испарения из системы выводится значительное количество влаги, в некоторых клетках остается мало вещества (до 1/3 от удельной массы клетки) и они «высыхают», то есть состояние клетки изменяется обратно в состояние «0» (воздух), а все остававшееся в ней вещество равномерно распределяется между её соседями, которые должны быть в состоянии «1» (жидкость). Если таких соседей не нашлось, клетка постепенно теряет всю влагу до конца и становится кристаллом (переходит в состояние «2»), происходит «усадка». Но этот процесс характерен только для клеток, находящихся на поверхности в прямом контакте с воздушными клетками. Кроме того, масса клетки-кристалла, получившейся в результате усадки, не может превышать массы клеток-кристаллов, получившихся в результате процесса кристаллизации в объема слоя.
Кристаллизация в слое происходит, если концентрация вещества в клетке достигает определенного пересыщения, значение которого вычисляется в зависимости от таких факторов, как температура раствора, положение клетки в пространстве, фазового состояния и положения соседей (1) [1]:
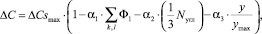(1)
где αi – коэффициенты в интервале (0...1); Nугл – количество угловых структур вокруг рассчитываемой клетки [шт]; ΣФ1 – количество клеток в фазовом состоянии 1 (жидкость) [шт.]; k и l – координаты клетки в окрестности рассчитываемой клетки; ymax – максимальная глубина слоя [шт. клеток]. Максимальное пересыщение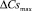 
рассчитывается по формуле 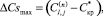(2):
(2)
где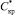 
– концентрация насыщенного раствора вещества покрытия, в зависимости от температуры [кг в-ва/кг раствора].
Угловая структура может состоять только из «твердых» клеток, т.е. клеток, которые находятся в состоянии «2» (затвердевшее вещество покрытия) или в состоянии «3» (вещество подложки).
Как только достигается необходимое пересыщение, клетка начинает забирать из соседних клеток вещество покрытия, необходимое для заполнения объема клетки кристаллом этого покрытия. В обмен клетка отдает им содержащуюся в ней влагу. Этот процесс идет тем быстрее, чем выше в клетке пересыщение. Принято допущение, что клетки с раствором, имеющие непосредственный контакт с воздухом, не кристаллизуются.
Уравнения математической модели клеточного автомата
Соотношения записываются для произвольного элемента расчетного пространства, который характеризуется в каждый момент времени следующими параметрами: массами содержащихся в нем компонентов (влаги и вещества покрытия) и фазовым состоянием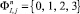 
.
Диффузия является следствием градиента концентраций в клетках, вызванной протекающими процессами кристаллизации и испарения.
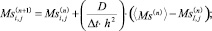
На основании второго закона Фика процесс диффузии компонентов для некоторой ячейки пространства можно описать следующими соотношениями 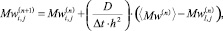(3):
(3)
где MS – масса вещества оболочки в клетке [кг]; MW – масса влаги в клетке [кг]; D – коэффициент диффузии [м2/с]; Δt – шаг по времени [c]; h – шаг по пространству (размер ячейки); n – индекс по времени; i, j – координаты рассчитываемой клетки на расчетном поле.
Первый член в круглых скобках соотношения (3) характеризует приход массы из соседних клеток, второй член – уход массы в соседние клетки (за счет диффузии).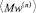 
, 
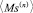– среднее арифметическое соответственно масс влаги и вещества покрытия в соседних клетках.
Неравномерность распределения вещества в системе обусловлена испарением и кристаллизацией, которые описываются уравнениями массопереноса.
На каждом шаге по времени происходит перенос масс компонентов по следующим законам:
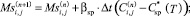(4)
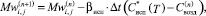(5)
где βкр, βисп, – кинетические параметры процессов кристаллизации и испарения соответственно;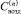 
– концентрация влаги в сушильном агенте (воздухе).
Перенос массы вещества в ячейку при кристаллизации учитывается уравнением (4); потеря воды из ячейки во время испарения с ее поверхности учитывается уравнением (5).
Соотношение для расчета концентрации раствора вещества покрытия в клетке имеет вид 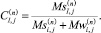(6):
(6)
Изменение влаги в реакторе описывается соотношением 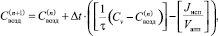(7).
(7)
где τ – среднее время пребывания сушильного агента в аппарате [c]; Cv – концентрация водяного пара в воздухе, подаваемом для сушки (масс. доля); Jисп – средняя скорость испарения со всех гранул [м3(влаги)/с]; Vапп – объем аппарата [м3].
Первое выражение в квадратных скобках отвечает за убывание массы влаги в воздухе аппарата за счет обдува сухим воздухом и откачки влажного. Второе выражение отвечает за увеличение массы влаги за счет испарения с поверхности всех гранул.
Уравнение (7) может быть записано в виде разностной схемы для клеточного автомата в виде выражения 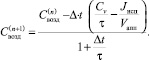(8):
(8)
Средняя скорость испарения в аппарате рассчитывается по формуле 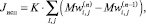(9)
(9)
где К – коэффициент масштабирования. Массовая и объемная доли влаги в покрытии определяются по соотношениям (10), (11):
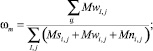(10)
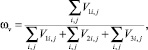(11)
где ωm и ωv – соответственно массовая и объемная доли влаги в оболочке. В соответствии с формулами (1)-(11) для каждой клетки рассчитываются:
– физико-химические свойства компонентов (плотность и концентрация раствора в клетке, его вязкость, растворимость вещества покрытия) [6],
– направление потока массы,
– возможность начала и конца процесса фазового перехода: фазовый переход для клетки осуществляется не мгновенно, для клеток, подверженных фазовым переходам, запускаются функции перераспределения масс по формулам (4)-(6), клетка меняет свое фазовое состояние только когда функции перераспределения веществ завершат свою работу.
Для реализации уравнений клеточного автомата был разработан программный модуль на языке С++ в платформе Linux.
Рис. 2. Визуализация расчетного поля
В результате применения программного модуля было получено «расчетное поле покрытия». Визуальная структура среза сформировавшейся оболочки представлена на рис. 2. На нём заметен образовавшийся раскол в покрытии из-за большой скорости испарения влаги с поверхности покрытия.
Были рассчитаны следующие параметры покрытия:
|
Толщина покрытия |
300 мкм |
|
Доля затвердевшего вещества покрытия (масс) |
0,26 |
|
Доля влаги в покрытии (масс) |
0,02 |
Результаты решения хорошо согласуются с экспериментальными данными, относительная погрешность не превышает 7 %.
Варьируя температуру сушильного агента и его объемный расход, были определены оптимальные значения параметров покрытия, характеризующиеся снижением массовой и объемной доли влаги в покрытии, а также его целостностью.
Работа выполнена в рамках государственного контракта № 11.519.11.4004 с Министерством образования и науки РФ.
Рецензенты:
Бессарабов А.М., д.т.н., профессор, заведующий учебно-научным комплексом, ФГУП «Государственный научно-исследовательский институт химических реактивов и особо чистых химических веществ «ИРЕА», г. Москва;
Куркина Е.С., д.ф.-м.н., ведущий научный сотрудник факультета ВМК, МГУ им. М.В. Ломоносова, г. Москва.
Работа поступила в редакцию 12.03.2013.