Электронные журналы возникли относительно недавно на почве широкого внедрения интернета, эксплуатируя его основное качество – скорость распространения информации. Потребность в удобочитаемом виде документов породила смешанные технологии, при которых текст хранится в формате PDF и близких к нему, а интерфейс доступа обеспечивается типичными для интернета средствами.
PDF непрерывно развивается, усилиями создателей математических пакетов алгоритмическая основа успешно переносится в интернет при помощи CDF – многообещающего формата исполняемых документов (Computable Document Format), XML-технология семантического WEB позволяет учесть требования электронных библиотек [1].
При всем разнообразии форм электронной документации, существуют электронные журналы, базирующиеся на оперативных возможностях современных браузеров. В интернете самым естественным образом возникли средства для отображения математической символики [2] и появилась своя алгоритмическая среда, развитая изначально для поддержки меню, но включающая в себя и математические операции.
Относительную неразвитость математического обеспечения на клиентской стороне сегодня легко поправить, опираясь на серверное математическое обеспечение. Иными словами, для придания электронным журналам дополнительных функций вовсе не обязательно дожидаться вытеснения PDF более развитым составом CDF, или, возможно так вернее будет выразиться, – не обязательно в CDF видеть реализацию только одной идеи на основе пусть неплохого, но, все же, одного математического пакета. Развивать альтернативные ветви вполне целесообразно.
В настоящей статье рассматриваются основные положения иной концепции – создания электронного журнала с исполняемыми алгоритмами и связи с акторами на основе технологии «живая книга» [3], а также реальный опыт авторов, внедренный в учебный процесс [4].
Развитие XML-формата FB2
Эпоха семантического WEB приносит нам книги и документы, читаемые на букридерах и смартфонах. Немалую роль в этом играют появившиеся и быстро распространившиеся правила оформления документов с выделенными XML-тэгами содержательными частями, как это делается в формате FB2.
Имеющиеся в интернете тэги оформления таблиц вполне подходят для передачи матриц, но они избыточно сложны. Поэтому рационально по образу и подобию того, что произошло в букридерах, предложить тэги для генерации, например, портретов матриц
<m> A = [[1,2],[3,4]]:опция </m>
Некоторое представление о характере рисунков, которые можно при этом увидеть, дают портреты М-матриц [5] Адамара (рис. 1), Мерсенна и Эйлера (рис. 2).
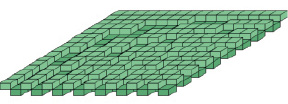
Рис. 1. Объемный портрет матрицы Адамара порядка 16


Рис. 2. Плоские портреты матрицы Мерсенна порядка 11 и Эйлера порядка 22
Анализ особенностей цветных объемных и плоских портретов матриц Адамара, Мерсенна, Эйлера и Ферма позволяет развивать содержательную теорию минимаксных ортогональных матриц [6, 7], помогает выявлять неизвестные закономерности и новые артефакты.
Очевидно, что с помощью таких матричных построителей можно не только передавать особенности научного исследования, но и вести таковое, поскольку это не просто иллюстратор, но и часть обычного обеспечения математического пакета, которая уже сегодня сделана достаточно мощной [8]. То же самое касается выводов графиков функций, пример одной из них приведен на рис. 3.
Отдельного рассмотрения требует техника записи в электронном журнале формул и индексов. В сети можно встретить итоги поспешной компиляции математических формул в формат gif, после чего математические записи теряют многое в своем качестве. Использование графических плагинов приводит к появлению в интернете безликих страниц, потому что не всем нравится идея ставить у себя эти плагины.

Рис. 3. Передача трехмерного графика
Компьютеры постепенно меняют стиль написания математических формул, наследуемый еще от практики употребления гусиного пера и стило. При помощи клавиатуры определение норм векторов в пространстве Rn проще написать, например, так:
||x||1 = Σi = 1:n |xi|;
||x||2 = (Σi = 1:n xi2)1/2;
||x||∞ = maxi = 1:n |xi|,
указывая границы индексов у сумм (и у интегралов, если понадобится) внизу, в строчку.
Не надо переусложнять нотацию, компьютерный мир пережил несколько революций, наиболее устойчивы к новациям простые текстовые форматы. Многие документы рациональнее оформлять в них, не исключено, что развитие браузеров снимет эту проблему самым естественным образом, ведь она общая. Формат, в котором реализованы указанные и многие другие возможности, развивающие и дополняющие формат FB2, авторы сочли возможным назвать FB2+.
Доработка языка матричных вычислений Java-Matlab
По неизвестным авторам причинам матричные операции не были включены в стандарт языка javascript. Эту ситуацию легко исправить, используя, например, двойные фигурные скобки {{...}} для выделения матричных выражений. Исполняемый в тексте сообщения алгоритм размещается между тэгами <math> {{матричные операции}} </math> .
С помощью предкомпилятора содержимое фигурных скобок транслируется с языка векторно-матричного исчисления в javascript, этому исполнению авторы дали название Java-MatLab. В его реализации определены все основные матричные операции: транспонирование {{X = A’}}, алгебраические сложение, умножение, левое {{A = A\B}} и правое {{X = B/A}} умножение на обратную матрицу, поточечные операции: произведение и деление Адамара {{X = A.*B; X = A./B}}. Всего реализовано до полусотни функций. С их помощью решаются стандартные задачи линейной алгебры, включая решение систем линейных алгебраических уравнений и алгебраическую проблему собственных чисел. Этот базис позволяет развернуть процедуры анализа и синтеза линейных динамических систем, метод Рунге-Кутта, частотный анализ систем и сигналов, безошибочное решение целочисленных систем уравнений [8]. Возможна организация и подключение пользовательских тулбоксов.
В описываемой реализации матричные формулы пишутся плотно, без пробелов. Функции размещаются за скобками, например, кронекерово произведение матриц выглядит как A = kron(B,C).
Все это исполняется на интернет-странице электронного журнала или электронной книги нисколько не хуже, чем в локальной среде, а последствия этого усовершенствования интернет-технологии самые впечатляющие. Собственно, в этом и состоит концепция CDF, но ее вовсе не обязательно, как отмечалось выше, связывать с одним каким-либо исполняющим ядром. С помощью предлагаемого синтаксиса математические вычисления, долгое время совершенно неоправданно не используемые, уже сегодня шагнули на научные и обучающие форумы и блоги. Такой софт обещает существенную экономию на дорогом лицензионном математическом обеспечении в школах и вузах по всей стране, и это вполне можно и нужно развивать в рамках федеральной программы.
Опыт внедрения математических пакетов прошлого показал, сколь эффективными могут быть реализации вычислительных методов линейной алгебры не с помощью библиотек FORTRAN-подпрограмм, но всего лишь с помощью удачного синтаксиса, передающего особенности языка матричного исчисления типа MatLab. И все это возможно и необходимо делать широко прямо сейчас, но уже в сети интернет. Подобные преобразования уже давно назрели.
Язык Java-MatLab и система его реализации, разработанные авторами и развитые в рамках выполнения НИР [9], внедрены в учебный процесс и используются на интернет-ресурсах, предназначенных для совместных исследований в сети [8, 10].
Связь электронного журнала с роботами
Электронные журналы обладают коммутативностью по отношению к внешним источникам информации, в частности, к сетевым роботам. Эта составляющая присутствует, например, на сайте разработчиков CDF-формата [11]. Помимо математических расчетов, система поставляет данные с обширной периферии датчиков – может измерить температуру в заданном районе мира, составить маршрут и расписать временные характеристики вылета и посадки реальных самолетов вдоль маршрута и т.п. Стоить отметить, что эта сторона многообещающая, прежним форматом журнальной или книжной продукции не затрагиваемая, но интересная и востребованная для нужд науки и обучения.
Наиболее перспективны для расширяемого связью с роботами электронного журнала беспроводные технологии и их сенсорные завершения, которые испытывают настоящий бум своего развития. Сегодня область сенсорных завершений делят между собой множество реализаций с использованием стандартов передачи данных Wi-Fi, Wi-MAX, Bluetooth, Wireless USB, ZigBee, Home RF и т.д.
Такие реализации, в отношении которых у авторов статьи накоплен богатый опыт, легко интегрируются с интернет и представляют собой основу низкоскоростных беспроводных сетей будущего с низким энергопотреблением, предназначенных для систем управления с большим количеством робототехнических узлов [4, 8].
Заключение
Создание физико-математической литературы традиционно сложнее создания художественной книги, журнала. Сетевой инструментарий позволяет максимально облегчить этот процесс за счет совмещения механизмов сети с обыденными издательскими нуждами: процессами рецензирования, редактирования, верстки, корректуры. На нижнем уровне реализации этих процессов рассматриваемое предложение значительно упрощает формирование текстовой части, формул и иллюстраций.
Иллюстративная мощность математической сети на основе технологии «живая книга» чрезвычайно высока, это удобный и простой для реализации принцип развития, который стоит вывести на уровень программ, призванных усилить позиции науки и образования в стране. Математические сети для реализации «живых книг» – эффективные инструменты для обеспечения научных исследований распределенных по территории страны коллективов, приоритет в их развитии имеет большое значение в рамках государственной технической политики.
Электронные журналы в форме интернет-страниц хороши своей мобильностью и при наличии обязательного рецензирования ничто не мешает таковым войти в перечень ВАК. Конечно, для принятия такого решения потребуется изменение требований в части обязательных сегодня тиража и распространения по подписке в пользу количества посещений по сети.
За рассматриваемыми технологиями будущее, и неверно принятые решения в отношении интегрированных мобильных форм могут иметь далеко идущие негативные последствия для науки. Это элементарно не выгодно. В то же время слишком низкий уровень освоения технологий, необходимых учреждению для того, чтобы войти в категорию издателей электронных журналов, создает предпосылки для появления вала некачественных предложений. Следует понять и реализовать механизмы рационального сдерживания.
Рассмотренная концепция создания математической сети на основе технологии «живая книга» реализована авторами и имеет несколько разновидностей и адресов в сети интернет [4, 8, 10], часть из которых внесены в каталог системы федеральных образовательных порталов Министерства образования и науки РФ [12].
Рецензенты:
Михайлов В.В., д.т.н., профессор, ведущий научный сотрудник лаборатории информационных технологий в системном анализе и моделировании, ФГБУН «Санкт-Петербургский институт информатики и автоматизации» Российской академии наук, г. Санкт-Петербург;
Юлдашев З.М., д.т.н., профессор, заведующий кафедрой биотехнических систем Санкт-Петербургского электротехнического университета, г. Санкт-Петербург.
Работа поступила в редакцию 07.03.2013.



