Актуальность исследования течения в канале с внезапным расширением определяется тем, что выявленные в данном простом случае режимы повторяются в более сложных технических устройствах, в которых также имеются отрывные течения. Например, это могут быть сопловые блоки, эжекторы, камеры сгорания со сверхзвуковым горением, фронтовые устройства двигателей гиперзвуковых летательных аппаратов (рис. 1).
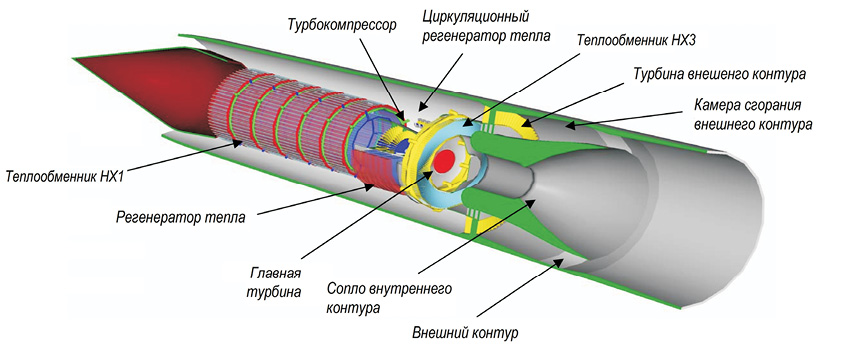
Рис. 1. Двухконтурный воздушно-реактивный двигатель с разрывом образующей сопла гиперзвукового летательного аппарата
Существуют и другие технические приложения течений с внезапным расширением (ТВР): внутренние отсеки вооружений летательных аппаратов, форсажные камеры двигателей со сверхзвуковым горением и т.п. Всех их объединяет одна общая техническая проблема – отрывное сверхзвуковое течение и связанное с ним донное давление.
Донным давлением называется среднее давление Рд в донной области, оно определяет картину течения вниз по потоку. В фундаментальном труде А. Гогиша и Ю. Степанова [1] теоретически и экспериментально изучены вопросы влияния неравномерности течения в донной области на качественный характер ТВР. Показано, что модель изобарического течения в донной области вполне удовлетворяет потребностям практики. Обзор экспериментальных работ по проблеме донного давления и история вопроса приведен в статье [2].
Исследования были проведены на установке, представленной на рис. 2.
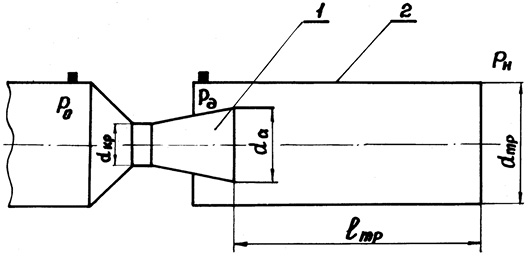
Рис. 2. Схема экспериментальной установки: 1 – сопло; 2 – цилиндрический канал
При заданной геометрии сопла и канала течение полностью определяется множествами газодинамических переменных f0 параметров торможения рабочего газа, истекающего из сопла, и fн – газа, заполняющего канал до начала истечения струи. Использованное экспериментальное оборудование позволило установить вид типичного графика зависимости Рд(Р0) донного давления от полного давления перед соплом, а также отыскать характерные давления РI–PIV (рис. 3) в заданном диапазоне чисел Маха и полууглов конусности сопел.
Рассмотрим теперь подробнее наиболее сложное явление, возникающее в канале с внезапным расширением потока – низкочастотные колебания. Они сопровождаются мощным акустическим излучением, что широко используется в различных технологических установках в области металлургии и упрочнения изделий из металлов. Нестационарные явления, сопровождающие истечение сверхзвуковой струи в канал с герметизированной донной областью, изучались в течение длительного времени [3–6] как экспериментально, так и с помощью разработанных математических моделей. Достаточно полный обзор экспериментальных исследований дан в статье [7]. Ниже приведено обобщение сведений о низкочастотных колебаниях в канале.
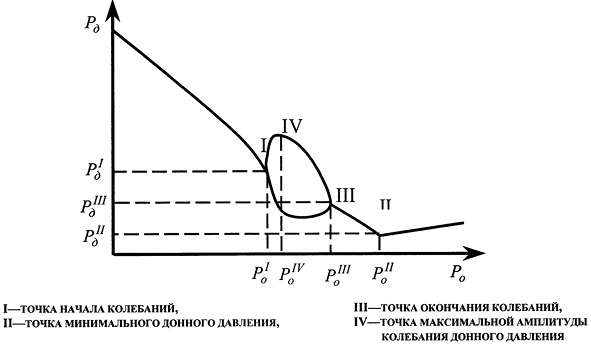
Рис. 3. Характерные давления на типичном графике зависимости Рд(P0)
Экспериментально обнаружены три вида низкочастотных колебаний [8], следующих по мере изменения Р0 друг за другом. Эти виды колебаний отличаются формой колебательного цикла и механизмом поддержания. При увеличении Р0 сначала возникают составные колебания, когда колебательный цикл составлен из двух полуциклов: часть колебательного цикла происходит при открытой донной области, в которую попадает газ окружающей среды, а другая при закрытой. С повышением Р0 за ними всегда следуют псевдогармонические колебания, подобные осциллятору Ван-Дер-Поля. Колебания происходят между двумя крайними положениями, соответствующими натеканию струи на стенку турбулентным участком и первой бочкой. Донная область – закрытая. Наконец, при дальнейшем росте Р0 устанавливаются релаксационные колебания, амплитуда которых расположена не симметрично (смещена вверх) относительно осредненной (построенной без учета колебаний) кривой графика Рд(Р0). Колебательный цикл имеет характерную пилообразную форму.
Низкочастотные колебания заканчиваются, как правило, вблизи точки графика, соответствующей минимальному донному давлению. Если в этот момент зафиксировать Р0, то произойдёт плавная перестройка ударно-волновой структуры струи и небольшое уменьшение Рд. Данный переходный процесс выражается в переходе точки натекания границы струи на стенку из области турбулентного участка в область первой бочки.
Результаты теоретического исследования низкочастотных колебаний
Колебания и понятие дисбаланса расходов. Авторами была разработана полуэмпирическая модель течения, а также введено понятие [9] дисбаланса расходов масс ζ = (qp – qv)/Qa, поступающих в донную область (qv) из окружающей среды или из области присоединения струи к стенке канала и эжектируемых из донной области струей (qp), отнесенный к расходу рабочего газа через сопло Qa. ζ является критериальной величиной, характеризующей состояние газодинамической системы в канале в целом. Если при заданном Р0 дисбаланс ζ равен нулю, то система находится в стационарном положении, в противном случае донное давление изменяется во времени. Изучение поведения газодинамической системы в пространстве переменных ζ – Рд аналогично исследованию ее динамических свойств на фазовой плоскости. Было установлено, что при натекании струи на стенку канала газодинамическим или турбулентным участком функция дисбаланса ζ(Рд) при Р0 = const в пределах своей области определения (ООФ) может быть немонотонной и иметь 2 корня, один из которых устойчивый, а другой ‒ нет (рис. 4). Устойчивому корню соответствует экспериментальное значение донного давления (показано на рис. 4 сплошной линией на нижней плоскости Р0 – Рд).
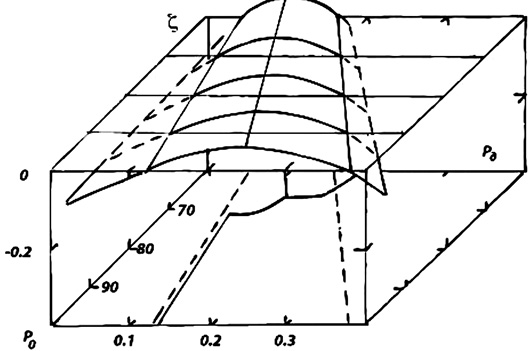
Рис. 4. Зависимость дисбаланса ζ от Рд и Р0
Если в ООФ функция ζ(Рд) не имеет корней, то при данном Р0 струя в канале не может находиться в стационарном положении. Существует такое сочетание геометрии сопла и канала, а также величины полного давления в ресивере перед соплом, что функция дисбаланса ζ(Рд) при Р0 = const в пределах своей области определения (ООФ) имеет только один корень. Колебания в таких системах не возникают.
Концепция дисбаланса расходов позволила не только построить полную классификацию режимов течения в канале с внезапным расширением [10], но и исследовать зарождение и окончание колебаний, процесс перестройки колебательных циклов.
Численное исследование колебаний донного давления. Основой всех двухпараметрических моделей турбулентности, использующих осреднение уравнений Навье-Стокса по Рейнольдсу, является гипотеза Буссинеска [11] о турбулентной (вихревой) вязкости. В сложных течениях, например, с большой кривизной линий тока или с отрывом и присоединением пограничных слоев, гипотеза не применима. Сверхзвуковые отрывные течения с донными областями как раз и относятся к такого рода случаям. Кроме того, непосредственно использовать данные модели турбулентности для расчета сверхзвуковых течений на нестационарных режимах нельзя, т.к. при их выводе используется осреднение параметров течения по времени. Однако низкочастотные колебания донного давления относятся к классу квазистационарных, т.е. таких, период которых существенно больше характерного времени протекающих газодинамических процессов. Это позволяет проводить по крайней мере исследование качественных характеристик колебательных режимов. Методика постановки вычислительного эксперимента подробно описана в статье [12].
Интересным результатом, полученным в ходе вычислительного эксперимента, является выявленный механизм перехода от составных колебаний к псевдогармоническим (рис. 5).

Рис. 5. Переход от составных колебаний к псевдогармоническимколебаниям. Р0 = 50 ати, Ма = 2, lтр = 342 мм
В ходе ранних экспериментальных исследований было выявлено, что при переходе от составных колебаний к псевдогармоническим меняется не только форма колебательного цикла, но иногда удваивается частота.
Сначала в колебаниях появляется новая мода, отражающая трансформации ударно-волновой структуры струи и перемещения центрального скачка уплотнения, затем постепенно уменьшается до нуля пик Рд, соответствующий открытой донной области (рис. 5 в левой части графика). При дальнейшем увеличении Р0 две моды колебаний в случае коротких каналов сливаются, а в средних и длинных полностью разделяются. При этом происходит удвоение частоты колебаний.
За псевдогармоническими следуют релаксационные колебания, имеющие характерную пилообразную форму цикла. При больших числах Ма струи имеют длинную первую бочку, а линии тока ‒ небольшую кривизну. В результате в момент касания первой бочкой стенок канала вторая застойная зона, образующаяся между сечением, соответствующим максимальному диаметру первой бочки струи, и областью натекания турбулентного участка на стенку канала, оказывается существенно длиннее, чем у струй с меньшим Ма, а ее объем сопоставим с объемом донной области. Колебания происходят в небольшом диапазоне изменения Рд и заключаются в возникновении и исчезновении второй застойной зоны.
Выводы
Низкочастотные колебания струи в канале с донной областью имеют период много больше характерного времени протекания турбулентных процессов в слое смешения. Это позволяет с определенными оговорками применять для их исследования численные методы, основанные на дифференциальных моделях турбулентности. Вычислительный эксперимент позволил подтвердить основные выводы о природе и механизме колебаний, сделанные ранее на основе экспериментальных исследований. Для выявления тонкой структуры колебательных циклов необходимо применение прямого численного моделирования или как минимум методов, построенных по типу моделирования крупных вихрей.
Рецензенты:
Баранов И.В., д.т.н., профессор, заместитель директора Института холода и биотехнологий, ФГБОУ «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики», г. Санкт-Петербург;
Пеленко В.В., д.т.н., профессор, заместитель директора по учебной работе Института холода и биотехнологий, ФГБОУ «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики», г. Санкт-Петербург.
Работа поступила в редакцию 14.02.2013.



