В процессе использования инструментов срочного рынка обязательно возникают некоторые побочные эффекты. Один из них – это риск применимости производных финансовых инструментов, который измеряется рядом показателей, обозначаемых в основном греческими буквами, именно поэтому не раз они в специализированной литературе и называются термином «греческие». Используемые обозначения не просто носят какой-то иносказательный характер, просто так сложилась рыночная практика, что показатели производных финансовых инструментов стали называться буквами греческого алфавита. Всеми участниками рынка это было воспринято как должное, и особых противоречий в практическом применении не возникло. В этой связи будет наиболее удобным и приемлемым рассмотреть более детально некоторые показатели производных финансовых инструментов, их экономический смысл и значение как для рынка, так и для экономики в целом. При этом проблема применимости показателей, эксплицированных из древнегреческого алфавита, будет довольно наглядно продемонстрирована [2].
Так, в общем и целом, несмотря на превалирование латинского алфавита, на рынке финансовых производных нашли своё применение именно греческие буквы. Первым из этих показателей является дельта (Δ, delta). В свою очередь дельта измеряет величину изменения стоимости данного инструмента V при незначительном либо малом изменении базисного ценового фактора S. Например, мы можем взять в качестве базисного актива ставку процента или цены базисного актива. Так, величина изменения стоимости финансового инструмента V может быть вычислена при помощи следующей формулы:
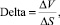 (1)
(1)
где ΔV – изменение стоимости финансового инструмента; ΔS – изменение стоимости базисного актива.
При этом, если изобразить зависимость стоимости инструмента от базового ценового фактора некой линейной зависимостью, допустим, простой линией, то дельта будет характеризовать угол наклона, при этом её величина должна быть равна тангенсу данного угла [1]. Следовательно, как и цена базисного пункта, так и дюрация, в том числе и дельта, будут отражать тот же самый риск, т.е. чувствительность стоимости инструмента V к изменению величины инструмента V, а также к изменению процентной ставки r. Более наглядно данный процесс мы можем показать на следующей формуле:
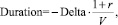 (2)
(2)
где Duration – величина чувствительности стоимости; Delta – отрицательное значение изменения цены финансового инструмента; r – изменение процентной ставки; V – величина финансового инструмента.
Таким образом, исходя из приведенной формулы, мы можем получить некое значение дюрации в виде набора цифр, по которому необходимо будет построить график. При анализе графика следует обратить особое внимание на изгиб получившейся линии. Так, если график ценового фактора будет представлен в виде прямой, то мы можем судить о постоянной величине дельты [5]. Но это будет идеальный для нас вариант, который в практической деятельности, как правило, не происходит.
На самом деле наиболее распространённым видится график переменной дельты, т.е. мы видим некую кривую линию с различными изгибами. При этом дельта может быть переменной и может меняться под действием факторов риска, в нашем случае это может быть дельта для опционов [3].
В то же время существуют показатели несколько другого рода. Например, показатель гамма (Г, gamma), который измеряет изменение дельты при изменении базисного ценового фактора. Вычисляется данный показатель по следующей формуле:
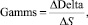 (3)
(3)
где ΔDelta – неизменно малое изменение цены стоимости базисного актива; ΔS – степень изменения базисного фактора.
Так, гамма позволяет измерить тот же риск, что и выпуклость. В частности, если график зависимости стоимости производного инструмента от базового ценового фактора будет «выпуклый», то значение гамма останется неизменно положительным; если при этом будет наблюдаться вогнутый график, то гамма будет иметь отрицательное значение. В случае получения прямой линии мы будем наблюдать нулевое значение показателя гамма. Следовательно, мы можем сделать вывод, что рассматриваемый показатель гамма имеет особую актуальность для опционов. В частности, наибольшее значение гамма может достигать для опционов, не предполагающих выигрыша (at-the-money), но гамма, близкая к нулю, характерна для опционов «с проигрышем» (out-of-the-money), равно как и с выигрышем (at-the-money). В общем и целом показатель гамма имеет некий нейтральный характер, который позволяет его использовать в различных целях при расчётах на рынке финансовых производных [6].
Другим не менее важным показателем рынка финансовых производных видится показатель, который может измерить также и волатильность финансового инструмента. В данном случае речь идёт о показателе вега. Вега (vega) – это ещё один показатель риска производных финансовых инструментов, который измеряет изменение стоимости инструмента при изменении волатильности базового ценового фактора. В частности, можно представить формулу для расчёта показателя вега:
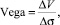 (4)
(4)
где ΔV –изменение базисного фактора; Δσ – изменение волатильности базового ценового фактора.
В общем и целом показатель вега работает довольно просто, при резком или внезапном изменении базового фактора, когда показатель Δ находится в запредельном значении, также с довольно большой амплитудой начинает изменяться значение волатильности базового ценового фактора. Это происходит во время возникновения и развития кризисных явлений на рынке.
Следующая совокупность показателей рынка финансовых производных может быть объединена показателями степени изменения значения базового актива.
Первым таким показателем нам видится показатель тета (θ, theta), который измеряет стоимость финансового инструмента при изменении срока, оставшегося до его исполнения. Более детально формула тета может быть представлена в следующем виде:
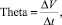 (5)
(5)
где ΔV – изменение базисного фактора; Δt – измерение временного промежутка, в течение которого происходит изменение величины базисного актива.
Таким образом, показатель тета позволяет нам сформировать мнение о том, каким образом будет изменяться цена базисного актива в течение определённого промежутка времени. Временной промежуток может иметь разную протяжённость, и поэтому его соотношение с величиной изменения базисного фактора может иметь далеко идущие последствия. Как следствие, данный показатель часто указывается инвестиционными компаниями в отчёте о прибылях и убытках. При этом такое его представление имеет некоторый статический характер и не способствует его адекватному анализу. Для более точного и приемлемого результата по этому показателю необходимо в знаменателе ставить не просто временное изменение, а величину, отражающую разницу между временным изменением и первоначальным состоянием, так скажем точкой отсчёта, о чём, впрочем, и говорит мировая практика [2]. В этом случае показатель тета будет иметь более практическое значение.
Следующим важным показателем для исследования рынка финансовых производных видится значение ро. Так, показатель ро (ρ, rho) очень часто используется для обозначения изменения стоимости процентных опционов при изменении процентной ставки. Вычисляется ро по следующей формуле:
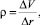 (6)
(6)
где ΔV – изменение базисного фактора; Δr – изменение процентной ставки.
Процесс изменения базисной цены базисного актива, который в данном случае играет роль стоимости процентных опционов, представляется весьма сложным и противоречивым. Подобный процесс не всегда зависим только от изменения процентной ставки. Если бы это было так, то нахождение изменения процентной ставки в знаменателе многое объясняло бы и не требовалось бы, иных корректирующих форм для получения приемлемого результата [7]. В подобном случае мы можем столкнуться с неадекватным и порой даже неверным результатом проведённых вычислений. В этом случае в знаменателе должна стоять сумма совокупностей изменения процентных ставок за определённый период времени.
В случае изменения данных стоимости опционов при изменении величины дивидендов мы можем обратиться к другому показателю. Так, для измерения риска доподлинно необходимо знать, какое значение будет показывать изменение стоимости опционов при изменении дивидендов. Такая величина существует – это лямбда (λ, lambda), которая может быть вычислена по следующей формуле:
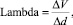 (7)
(7)
где ΔV – это изменение базисного фактора; Δd – изменение величины дивидендов для опционов на акции или уровня валютной процентной ставки в случае с валютными производными (свопами).
В случае с измерением лямбды мы имеем подобную картину, как и в предыдущих вариантах, т.е. мы с успехом брали в числителе изменение базисного фактора, при этом особо не задумываясь о его корреляционной связи с экономическим значением знаменателя. Так и в данный момент мы хотим получить приемлемое решение, но знаменатель заведомо берём «из прошлого», т.е. он у нас, несмотря на долю изменчивости, остаётся стабильным показателем по сравнению с изменяющимся числителем. В подобном случае изменение величины дивидендов Δd должно быть взвешено на количественную составляющую, которая должна быть характеристическим параметром количественной составляющей дивидендов или валютных производных инструментов. Только в этом случае мы получим не стабильную (статическую) характеристику рынка, а вполне динамический показатель.
Другим не менее важным показателем изменения состояния рынка финансовых производных представляется значение изменения скорости цены базисного актива. Данный показатель носит название «скорость» (speed) и в некоторых источниках обозначается греческой буквой омега (ω, omega).
Формула для расчёта скорости выглядит следующим образом:
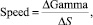 (8)
(8)
где ΔGamma – изменение показателя delta в определённый период времени; ΔS – степень изменения базисного фактора.
В данном случае необходимо отметить, что если дельта – это первая производная функция стоимости инструмента по базисному ценовому фактору, то именно гамма представляется как вторая производная, а скорость изменения цены – это уже будет производная третьего порядка. Данный показатель, т.е. скорость изменения гаммы и дельты при работе с опционами, характеризует уровень стабильности рынка. Безусловно, идеальным этот показать мы не назовём, но тенденцию и динамику изменения цен мы проследить вполне сможем. При этом возникает вопрос: каким образом и с какой динамикой будет меняться степень базисного актива? Пока на этот вопрос корректного ответа нет [6].
На заключительном этапе нашего исследования мы рассмотрим ряд более высоки показателей, которые характеризуют степень изменения более сложных составляющих величин по отношению к рыночному движению.
Так, первым из таких показателей представляется цвет (color). Данный показатель показывает изменение гаммы по мере изменения времени до исполнения контракта. Рассчитывается color по следующей формуле:
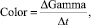 (9)
(9)
где ΔGamma – изменение дельты за определённый промежуток времени; Δt – изменяющийся промежуток времени, в рамках которого проводились измерения.
В частности, при всей противоречивости представленной формулы мы можем наблюдать, что рассматриваемый показатель показывает небольшие изменения цены базисного актива, которые могут повлиять на хеджирование контракта при его приближении к моменту исполнения [8, Р. 310]. Однако при всех положительных моментах рассмотренной формулы мы опять же видим несостоятельность знаменателя, которая может вылиться в некорректный результат работы всей формулы.
Следующим показателем, который может характеризовать положение на рынке, является показатель вомма (vomma). Данная величина отражает чувствительность значения переменной вега к изменению предполагаемой волатильности опциона. Вомма рассчитывается по следующей формуле:
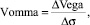 (10)
(10)
где ΔVega – изменение риска производных финансовых инструментов; Δσ – изменение волатильности базового ценового фактора.
Мы видим, что показатель вомма – это сложноструктурированная переменная, которая является второй производной от стоимости инструмента по базисному ценовому фактору.
Ещё одним значимым показателем в структуре индикаторов рынка производных финансовых инструментов является показатель вонна (vonna), который рассчитывается по формуле:
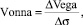 (11)
(11)
где ΔVega – изменение риска производных финансовых инструментов; Δσ – это изменение волатильности базового ценового фактора.
В общем и целом показатель вонна должен измерять чувствительность веги к изменению ценового фактора на рынке, что имеет очень важное значение как для индивидуального инвестора, так и для рыночного показателя в общем.
Следует сразу отметить, что показатели вомма и вонна используют при операциях с «экзотическими» финансовыми производными [9, с. 659].
Таким образом, на сегодняшний день мы можем констатировать несколько фактов. Так, на рынке финансовых производных существует большое количество индикаторов, неких значений, которые либо дублируют друг друга, либо не отражают той полноты информации, которая необходима рынку. Как следствие, на рынке возникают неоправданные риски, которые зачастую связаны далеко не с рыночной ситуацией, а просто с некорректным применением не всегда оправданных эконометрических формул. Для рынка финансовых производных эта проблема видится особенно острой, и вопросы применимости и адекватности тех или иных формул должны быть пересмотрены в самое ближайшее время.
Рецензенты:
Иваницкий В.П., д.э.н., профессор кафедры финансовых рынков и банковского дела Уральского государственного экономического университета, г. Екатеринбург;
Марамыгин М.С., д.э.н., профессор, заведующий кафедрой финансовых рынков и банковского дела финансовых рынков и банковского дела Уральского государственного экономического университета, г. Екатеринбург.
Работа поступила в редакцию 16.01.2013.



