Прохождение электрического тока через границу «электрод‒электролит» – сложный многостадийный процесс. Достаточно хорошо этот процесс описан в классической электрохимии для области равновесных потенциалов при прохождении постоянного тока. В этих условиях параметром, с помощью которого может быть рассчитана величина энергии, локализуемой в приэлектродном слое, является напряжение. Область сложных малоисследованных процессов начинается при выходе за пределы интервала потенциалов ±4 В, достигая значений ±1000 В. Особый интерес и наибольшую сложность представляют процессы при импульсном прохождении электрического тока. Очевидно, что в таком режиме, сочетающем импульсный характер тока и область высоких поляризационных напряжений, процесс является неравновесным, и, соответственно, его описание термодинамическими уравнениями не представляется корректным. В рассматриваемом режиме невозможно использовать в качестве меры энергии, вкладываемой в приэлектродный слой, величину поляризационного потенциала.
Цель исследования – определить физическую величину, являющуюся мерой энергетического воздействия на границу раздела сред, которая в свою очередь будет определять закономерности физико-химических процессов.
Проведение фундаментальных исследований в области импульсного электровоздействия на границу раздела фаз является особенно актуальным вследствие того, что данный режим, по сведениям ряда источников [1–5], является наиболее экономичным для осуществления воздействия на материалы энергетическими потоками с целью модификации их свойств и синтеза новых материалов. Наиболее изученной сферой применения данного типа процессов является формирование керамических покрытий на изделиях из сплавов вентильных металлов в микроплазменном режиме. Проведение фундаментальных исследований в данном направлении, развитие адекватных физико-химических моделей позволят заложить основы для создания принципиально новых технологий.
Рассматриваемый режим электровоздействия является импульсным, значения потенциалов лежат в интервале 100–1000 В. В данных условиях термодинамически разрешены практически все возможные электрохимические реакции. Пространственная область, в которой происходит интенсивная убыль носителей зарядов – ионов ‒ и которая характеризуется высоким омическим сопротивлением, называется барьерным слоем. Толщина барьерного слоя δ соответствует величине диффузионного слоя и зависит от условий поляризации границы раздела фаз.
Стадия электрохимических реакций является быстрой, поэтому стадией, лимитирующей скорость процесса в целом, является доставка реагирующих ионов в приэлектродный слой. Необходимость учета конвективного переноса минимальна, поскольку для импульсных процессов конвекционные потоки практически не затрагивают область диффузионного слоя.
В случае, когда лимитирующей стадией процесса является доставка, его скорость определяется диффузией и миграцией. В настоящей работе моделирование будет проводиться для симметричного электролита, что позволяет использовать в расчетах величину эффективного коэффициента диффузии.
При моделирование параметров энергетических потоков были сделаны следующие допущения:
– режим электровоздействия – потенциостатический;
– пропускание электрического тока через границу раздела фаз вызывает протекание электрохимических реакций и изменение концентрации реагирующих ионов в приэлектродном слое;
– концентрация реагирующих ионов непосредственно на поверхности электрода в начальный момент времени стремится к нулю вследствие разряда ионов;
– длительности импульсов тока таковы, что концентрационные изменения не выходят за пределы гидродинамического диффузионного слоя (слоя Прандтля);
– в течение рассматриваемого времени процессы концентрации компонентов в объеме раствора не изменяются;
– материал электрода является инертным;
– теплообмена между слоями в процессе прохождения электрического тока не происходит, процесс в течение рассматриваемой длительности импульса является адиабатным;
– процессы рассматриваются без учета плазменных превращений.
Скорость электродных процессов определяется градиентом концентраций на границе раздела фаз:
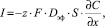 (1)
(1)
где z – число электронов, участвующих в электродной реакции; F – постоянная Фарадея; Dэф – эффективный коэффициент диффузии; S – площадь границы раздела электрод – раствор электролита.
Величина удельного сопротивление барьерного слоя ρ зависит от природы электролита и распределения концентраций, а значит, длительности пропускания тока t. Падение напряжения в приэлектродном слое определяется величиной тока и величиной сопротивления, а величина тока также зависит от изменения концентрации реагирующих ионов.
Запишем выражение для падения напряжения в приэлектродном слое:
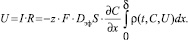 (2)
(2)
Мгновенная плотность энергии определяется соотношением:
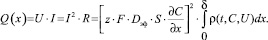 (3)
(3)
На основе второго закон Фика, с учётом граничных и начальных условий в работе [1] с помощью преобразования Лапласа найдено решение, описывающее концентрационные распределения в приэлектродном слое в зависимости от времени электровоздействия.
Данное решение имеет вид:
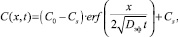 (4)
(4)
где Cs – концентрация ионов на поверхности электрода; C0 – концентрация ионов в объеме раствора.
Величина проходящего через электрод тока для потенциостатического режима определяется соотношением:
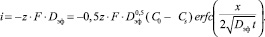 (5)
(5)
Из графика распределения тока в зависимости от времени его прохождения (рис. 1) видно, что максимальная плотность тока сосредоточена на границе раздела фаз и соответствует длительности электровоздействия в пределах 200 мкс.
Запишем распределение удельной электропроводности в приэлектродном слое:
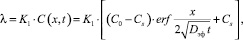 (6)
(6)
где К1 – коэффициент пропорциональности.
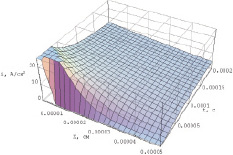
Рис. 1. Зависимость плотности тока I (А/см2) от расстояния x (см) и времени прохождения электрического тока t (с)
Представим распределение электропроводности в приэлектродном слое в зависимости от расстояния и времени импульса. Для этого примем следующие условия: электролит – раствор хлорида калия, C0 = 1 моль/л, Dэф = 10–5 см2/с, Cs = 0,0001 моль/л, К1 = 0,7397 л/(Ом∙см∙моль). График распределения удельной электропроводности приведен на рис. 2. Минимальной электропроводностью обладает приэлектродный слой с толщиной не более 1 мкм. При приближении к границе раздела электропроводность электролита уменьшается.
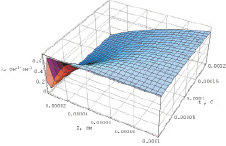
Рис. 2. Распределение электропроводности в приэлектродном слое в зависимости от расстояния и длительности импульса
Уравнение для удельного омического сопротивления с учётом электропроводности и концентрационных изменений можно записать в виде:
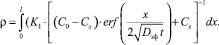 (7)
(7)
Интегрирование уравнения (7) позволяет определить зависимость удельного сопротивления слоя от времени и толщины слоя l. Графическое решение показало, что удельное сопротивление интенсивно изменяется на расстоянии до 5 атомных единиц (толщина моноатомного слоя составляет 10–10 см) и возрастает со временем.
Распределение мгновенной плотности энергии в слое от 0 до l, соответствующей единице поверхности, определяется соотношением:
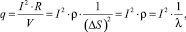 (8)
(8)
где V – объём.
Запишем выражение, описывающее распределение плотности энергии:
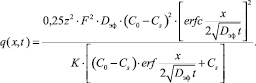 (9)
(9)
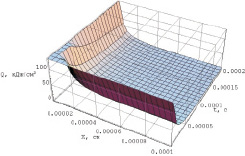
Рис. 3. Распределение плотности энергии в зависимости от времени и толщины барьерного слоя
Графически распределение плотности энергии вблизи границы раздела фаз представлено на рис. 3. Чем ближе к границе раздела фаз, тем выше величина локализуемой энергии. С уменьшением времени пропускания тока плотность энергии возрастает.
Для визуализации зависимости скорости процессов в приэлектродном слое от энергетического вклада на основе параметрических уравнений было построено распределение плотности тока в зависимости от энергии и времени электровоздействия (рис. 4).
В приэлектродном пространстве можно выделить две характерные области. Первая область, расположенная ближе к поверхности электрода, способна локализовать энергию в значительно большей степени, чем область, находящаяся на некотором расстоянии от электрода. Таким образом, показано, что распределение энергии для импульсного режима электровоздействия подобно структуре двойного электрического слоя, представления о которой развиты в классической электрохимии.
Рассчитанные параметры энергетических потоков для нестационарных импульсных процессов на границе раздела фаз позволяют говорить о том, что длительность импульса напряжения является основным инструментом управления процессом локализации энергии на этапе до возникновения стадии разряда. Сама величина энергии значительно превышает энергию химической связи, например, в молекуле воды (Eсв = 497,02 кДж/моль [5]). Что, очевидно, приведет к разрыву химических связей, ионизации приэлектродного пространства и началу плазменного процесса.
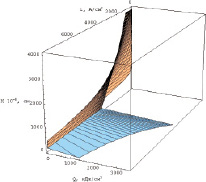
Рис. 4. Распределение плотности тока в зависимости от времени,толщины барьерного слоя и локализованной энергии
Данный вывод подтверждается визуальными наблюдениями в условиях воздействия на границу раздела фаз металл‒раствор электролита единичными импульсами с амплитудой напряжения от 250 В и длительностью от 100 мкс. Причем начало микроплазменного процесса можно наблюдать как в анодном, так и катодном режиме пропускания тока.
Выводы
1. В результате математического моделирования показано, что наибольшее изменение электропроводности электролита происходит в приэлектродном слое толщиной меньше микрона в течение нескольких микросекунд, причем чем меньше расстояние от поверхности электрода, тем электропроводность ниже.
2. С помощью решения граничной задачи показано, что распределение плотности энергии имеет зависимость от времени и расстояния от границы раздела фаз. Чем ближе к физической границе, чем меньше толщина слоя у границы раздела, тем величина энергии становится выше. С уменьшением времени воздействия (длительности импульса) плотность энергии резко увеличивается, соответственно, длительность токового импульса является наряду с величиной напряжения, плотностью тока, температурой и концентрацией фактором управления локализацией энергии.
3. Показано, что распределение тока в зависимости от величины локализуемой энергии и времени электровоздействия имеет две характерные области. Первая область, расположенная ближе к поверхности электрода, способна локализовать энергию в значительно большей степени, чем область, находящаяся на некотором удалении от электрода.
4. Импульсное электровоздействие на границу раздела фаз позволяет осуществлять управляемую локализацию энергию, причём на уровне, превышающем энергии связи для большинства известных веществ. Таким образом, закладываются физико-химические основы процессов, в которых возможно управляемо осуществлять разрыв одних химических связей при сохранении других.
Рецензенты:
Матюха В.А., д.т.н., профессор кафедры химии и технологии материалов современной энергетики СТИ НИЯУ МИФИ, г. Северск;
Мамаева В.А., д.т.н., с.н.с. лаборатории методов нанесения покрытий ИФПМ СО РАН, г. Томск.
Работа поступила в редакцию 29.01.2013.



