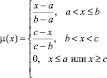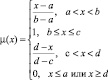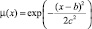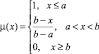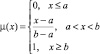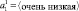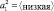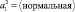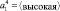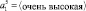Многочисленные попытки автоматизировать управление цементной печью с использованием методов классической теории управления оказываются неэффективными из-за большой нелинейности задачи, а также трудностей учета различных возмущений, с одной стороны. С другой стороны, с этой непростой задачей справляется опытный машинист-оператор. Наблюдая за деятельностью оператора, можно заметить, что он управляет печью на основе некоторых рассуждений. Задача управления процессом обжига клинкера может быть рассмотрена как задача принятия решений с использованием нечеткой базы знаний.
Различные по физическому смыслу задачи принятия решений, возникающие в управлении [1, 3, 6], сводятся к идентификации нелинейных объектов с одним выходом и многими входами, которые можно рассмотреть на основе языка продукционных правил, методов нечеткой логики и теории нечеткого управления.
Продукционные правила характеризуют взаимосвязь переменных «вход-выход» в виде экспертных высказываний: ЕСЛИ <входы> , ТО <выход> , представляющих собой нечеткие базы знаний [5]. Экспертные высказывания целесообразно свести к форме нечетких множеств, что позволит разработать систему нечеткого вывода, являющуюся генератором нечетких заключений об управляющем воздействии на объект.
Цель исследования – построить функции принадлежности нечетких множеств входных переменных, характеризующих состояние цементной печи и представляющих собой нечеткую базу знаний. На основе полученных функций принадлежности в дальнейшем можно синтезировать систему нечеткого вывода для регулятора расхода газа в системе управления обжигом цементного клинкера.
Материалы и методы исследования
Методика исследования состоит в представлении знаний при помощи языка продукционных правил и обработке их с помощью методов теории нечетких множеств.
Идея, лежащая в основе формализации причинно-следственных связей между переменными <входы-выход>, состоит в описании этих связей на естественном языке с применением теории лингвистических переменных [4, 5].
Нами рассматривается объект с одним выходом и входами вида:
y = fy(x1, x2, ..., xn), (1)
где y – выходная переменная; x1, x2, ..., xn – входные переменные.
Эти рассуждения можно преобразовать в систему продукционных правил ЕСЛИ <входы>, ТО <выход>, в которых входные и выходные переменные оцениваются словесными (нечеткими) термами.
Входные переменные:
• Влажность сырья (очень низкая, низкая, нормальная, высокая, очень высокая),
• Температура в пыльной камере (низкая, нормальная, высокая),
• Температура в зоне цепей (низкая, нормальная, высокая),
• Температура в зоне теплообменника (низкая, нормальная, высокая),
• Разрежение в пыльной камере (пониженное, нормальное, повышенное),
• Разрежение в головке печи (пониженное, нормальное, повышенное).
Выходная переменная:
• Расход газа (низкий, средний, высокий).
С использованием этих переменных и их лингвистических оценок можно записать набор правил, которые выражают алгоритм деятельности опытного машиниста-оператора.
Нечеткая база знаний представляет собой совокупность правил ЕСЛИ <входы>, ТО <выход>, которые отражают опыт эксперта и его понимание причинно-следственных связей в рассматриваемой задаче принятия решения. Примером экспертного правила из нечеткой базы знаний в задаче управления печью служит следующее высказывание:
ЕСЛИ Влажность сырья нормальная И Температура в пыльной камере нормальная,
И Разрежение в пыльной камере нормальное, ТО Расход газа средний.
Особенность подобных высказываний состоит в том, что их адекватность не изменяется при незначительных колебаниях условий эксперимента. Поэтому формирование нечеткой базы знаний можно трактовать как аналог этапа структурной идентификации [5], на котором строится грубая модель объекта с параметрами, подлежащими настройке. В данном случае настройке подлежат формы функций принадлежности, с помощью которых оцениваются входы и выходы объекта.
Итак, определим входные и выходные переменные нашей системы:
X1 <Влажность сырья>,
X2 <Температура в пыльной камере>,
X3 <Температура в зоне цепей>,
X4 <Температура в зоне теплообменника>,
X5 <Разрежение в пыльной камере>,
X6 <Разрежение в головке печи>.
Выходная переменная:
Y <Расход газа>.
Все переменные системы имеют количественное измерение. Для них предполагаются известными области изменения:
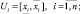
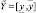, (2)
где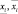 
– нижнее и верхнее значения входной переменной xi, а 
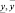– нижнее и верхнее значения выходной переменной Y.
Пусть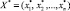 
– вектор фиксированных значений входных переменных рассматриваемого объекта, где 
, 
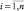. Задача принятия решения состоит в том, чтобы на основе информации о векторе входов X*определить выход y* ∈ Y. Необходимым условием формального решения такой задачи является наличие зависимости (1). Для установления этой зависимости будем рассматривать входные переменные xi, 
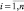и выходную переменную y как лингвистические переменные [3], заданные на универсальных множествах (2).
Для оценки лингвистических переменных Xi и Y будем использовать качественные термы из следующих терм-множеств:
A1 = {<очень низкая>, <низкая>,<нормальная>, <высокая>, <очень высокая>}
A2 = {<низкая>, <нормальная>, <высокая>}
A3 = {<низкая>, <нормальная>, <высокая>}
A4 = {<низкая>, <нормальная>, <высокая>}
A5 = {<пониженное>, <нормальное>, <повышенное>}
A6 = {<пониженное>, <нормальное>, <повышенное>}
D = {<низкий>, <средний>, <высокий>},
где Ai – терм-множество переменной Xi, D – терм-множество переменной Y.
Пусть 
– p-й лингвистический терм переменной Xi, dj – j-й лингвистический терм переменной Y.
Лингвистические термы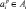 
и dj ∈ D будем рассматривать как нечеткие множества, заданные на универсальных множествах Ui и 
, определенных соотношением (2).
Нечеткие множества 
и dj определим соотношениями:
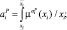
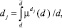(3)
где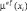 
– функция принадлежности значения входной переменной 
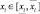терму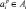 
, 
; 
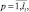
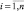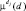– функция принадлежности значения выходной переменной 
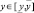терму решению dj ∈ D, 
.
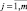По определению [2], функция принадлежности (ФП) μT(x) характеризует субъективную меру (в диапазоне [0, 1]) уверенности эксперта в том, что четкое значение x соответствует нечеткому терму T. Функции принадлежности удобно задавать в параметрической форме [7]. В этом случае задача построения функции принадлежности сводится к определению ее параметров. Наибольшее распространение в практических приложениях получили треугольные, трапециевидные и колоколообразные (гауссовы) функции принадлежности (табл. 1).
Таблица 1
Наиболее распространенные функции принадлежности
|
Наименование функции |
Аналитическое выражение |
Интерпретация параметров |
|
Треугольная |
|
(a, c) – носитель нечеткого множества – пессимистическая оценка нечеткого числа; b – координата максимума – оптимистическая оценка нечеткого числа |
|
Трапециевидная |
|
(a, d) – носитель нечеткого множества – пессимистическая оценка нечеткого числа; [b, c] – ядро нечеткого множества – оптимистическая оценка нечеткого числа |
|
Гауссова |
|
b – координата максимума; с – коэффициент концентрации |
|
Z-образная |
|
a – координата максимума; b – координата минимума |
|
S-образная |
|
a – координата минимума; b – координата максимума |
Результаты исследования и их обсуждение
Результатами исследований являются теоретические функции принадлежности, заданные в параметрической и графической формах, расчеты для получения которых будут описаны далее.
Определим функции принадлежности для термов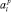 
и dj лингвистических переменных Ai и D. Рассмотрим лингвистическую переменную A2, определяющую значения входной переменной X2 <Температура в пыльной камере> . Терм-множество лингвистической переменной A2 выглядит следующим образом:
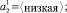
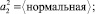
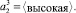
В качестве универсального множества U2 выберем диапазон разумно возможных значений переменной X2 U2 = [200; 300]. Для обеспечения компактного хранения нечетких множеств и удобства вычисления результатов арифметических операций над ними будем использовать кусочно-линейные функции принадлежности.
Итак, определим функцию принадлежности значений переменной X2 нечеткому множеству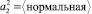 
. Воспользуемся трапециевидной формой функции принадлежности (см. табл. 1). Значения параметров a, b, c, d определяются экспертами. В данном случае: a = 230, b = 238, c = 242, d = 250.
Получим следующее выражение:
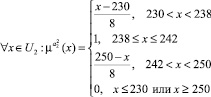(4)
Теперь рассмотрим нечеткое множество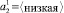 
. Наибольшей принадлежностью данному нечеткому множеству обладают «крайние» левые элементы универсального множества U2. Для их представления удобно использовать кусочно-линейную Z-образную функцию принадлежности.
Параметры a и b принимают следующие значения: a = 230, b = 238.
Аналитическое выражение функции принадлежности принимает следующий вид:
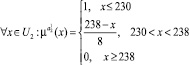(5)
Теперь рассмотрим нечеткое множество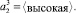 
Наибольшей принадлежностью данному нечеткому множеству обладают «крайние» правые элементы универсального множества U2. Для их представления удобно использовать кусочно-линейную S-образную функцию принадлежности. Параметры a и b принимают следующие значения: a = 242, b = 250.
Аналитическое выражение функции принадлежности принимает следующий вид:
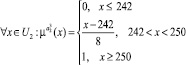(6)
Для удобства описания функций принадлежности всех нечетких термов лингвистической переменной A2 будем использовать 4 параметра a′, b′, c′, d′, определяемых экспертами. При этом для вспомогательных параметров ФП будем использовать следующие значения:
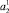: a = a′; b = b′;
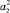: a = a′; b = b′; c = c′; d = d’;
: a = c’; b = d′.
Аналогичным образом зададим термы лингвистических переменных A3, A4, A5, A6, D. Результаты приведены в табл. 2.
Таблица 2
Параметры функций принадлежности лингвистических переменных
|
Лингвистическая переменная |
Параметры функций принадлежности |
|||
|
a′ |
b′ |
c′ |
d′ |
|
|
A2 <Температура в пыльной камере> |
230 |
238 |
242 |
250 |
|
A3 <Температура в зоне цепей> |
440 |
460 |
470 |
490 |
|
A4 <Температура в зоне теплообменника> |
550 |
572 |
588 |
610 |
|
A5 <Разрежение в пыльной камере> |
144 |
154 |
160 |
170 |
|
A6 <Разрежение в головке печи> |
3.6 |
4.6 |
5.4 |
6.4 |
|
D <Расход газа> |
12 700 |
12 900 |
13 100 |
13 300 |
Графики ФП термов лингвистических переменных A2, A3, A4, A5, A6, D аналогичны по своей форме. График функции принадлежности A2 представлен на рис. 1.
Теперь рассмотрим терм-множество переменной A1. Влажность сырья оказывает наибольшее влияние в процессе принятия решения относительно управления расходом топлива. Поэтому лингвистическая переменная A1 может принимать одно из 5 значений из следующего терм-множества (табл. 3). Универсальное множество U1 представляет собой диапазон значений входной переменной X1.
U1 = [38 %; 48 %].
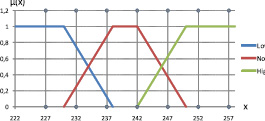
Рис. 1. Функции принадлежности нечетких термов лингвистической переменной A2
Таблица 3
Функции принадлежности термов лингвистической переменной A1
|
Обозначение |
Форма ФП |
Параметры ФП |
|
|
Z-образная |
a = 41; b = 42 |
|
|
треугольная |
a = 41; b = 42; c = 43 |
|
|
треугольная |
a = 42; b = 43; c = 44 |
|
|
треугольная |
a = 43; b = 44; c = 45 |
|
|
S-образная |
a = 44; b = 45 |
Для задания термов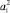 
, 
, 
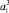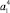будем использовать треугольные ФП (см. табл. 1). Для лингвистических термов 
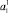и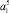 
, описывающих «крайние» значения из интервала U1, воспользуемся соответственно Z-образной и S-образной ФП (см. табл. 2). Результаты приведены в табл. 3. Графики функций представлены на рис. 2.
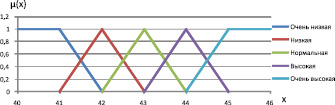
Рис. 2. Функции принадлежности нечетких термов лингвистической переменной A1
Вывод
Подход с позиции нечетких множеств является одним из способов для решения задачи управления сложными технологическими объектами. Применение теории нечеткого управления процессом обжига клинкера в цементной печи позволит моделировать поведение человека – эксперта, управляющего объектом, не знающего его математической модели. Построенные функции принадлежности представляют собой нечеткую базу знаний, хранящую информацию о правилах управления процессом, на основе которой можно синтезировать систему нечеткого вывода для регулятора управления подачей газа в цементную печь. Для построения более точных функций принадлежности можно расширить терм-множества используемых лингвистических переменных либо использовать другие формы функций принадлежности нечетких переменных.
Рецензенты:
Магергут В.З., д.т.н., профессор кафедры технической кибернетики, заместитель директора по научной работе, Белгородский государственный технологический университет им. В.Г. Шухова, г. Белгород;
Классен В.К., д.т.н., профессор кафедры технологии цемента и композиционных материалов, Белгородский государственный технологический университет им. В.Г. Шухова, г. Белгород.
Работа поступила в редакцию 21.01.2013.