Струйные аппараты очень широко применяются практически во всех отраслях промышленности: в энергетике, в теплофикационных установках, холодильных установках, в водопроводных установках, для транспортировки жидких и твердых материалов. Струйные аппараты успешно применяются для насыщения воды и безалкогольных напитков различными газами, например, диоксидом углерода или кислородом [1, 2, 3].
Основным принципиальным качеством струйных аппаратов (рисунок) является повышение давления инжектируемого потока без непосредственной затраты механической энергии.
Для характеристики в струйном аппарате двухфазного потока, состоящего из жидкой и газовой фаз, применяются следующие показатели [5]:
φ – объемная концентрация фазы, численно равная отношению объема, занимаемого фазой, к общему объему двухфазной среды.
Очевидно, что
φр + φг = 1, (1)
где φр и φг – соответственно объемные концентрации жидкой и газовой фаз; Х – массовая концентрация фазы, численно равная отношению массы фазы в единице объема к массе двухфазного потока.
xр + xг = 1. (2)
Плотность двухфазного потока определяется по зависимости
ρ = ρрφр + ρгφг = 1. (3)
Процессы при сатурации безалкогольных напитков в струйном аппарате отличаются сложностью, наличием нескольких зон, зависимостью от многих факторов. Поэтому примем следующие упрощения для потоков в камере смешения.
Двухфазный поток в камере смешения делится на 2 участка: начальный и зону молочно-белой эмульсии. Длина начального участка известна и задается экспериментальными уравнениями.
По длине начального участка струя сохраняет циклическую форму, диаметр ее равен диаметру рабочего сопла.
1. Статическое давление постоянно по сечению камеры смешения.
Oсновные уравнения, которым подчиняется работа, струйного аппарата: законы сохранения массы, импульса и энергии.
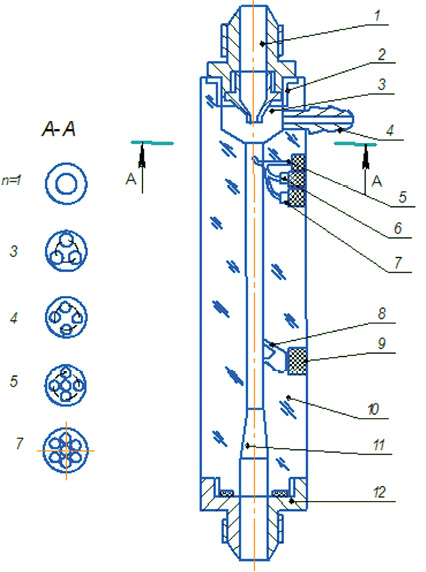
Принципиальная схема струйного аппарата:1 – входной штуцер; 2 – рабочее сопло; 3 – приемная камера; 4 – патрубок отвода газа; 5 – игла шприца; 6 – газовая камера сепаратора; 7 – жидкосная камера сепаратора; 8 – капиляр для отвода газа; 9 – резиновая прокладка; 10 – корпус струйного аппарата; 11 – диффузор; 12 – штуцер отвода насыщенной рабочей жидкости
Запишем эти уравнения в дифференциальной форме.
2. Уравнения неразрывности [5]
для газовой фазы:
(4)
для жидкой фазы:
(5)
3. Уравнение сохранения импульса [5]:
для газовой фазы
(6)
для жидкой фазы:
(7)
где F – сила трения на поверхности раздела жидкостной струи и газовой фазы.
Скорость газовой фазы на выходе в камеру смешения определяется по уравнению
(8)
Значение величины φг определяется по заданному значению основного геометрического параметра
(9)
Сила трения на поверхности раздела фаз, отнесенная к единице длины,
(10)
где сf – коэффициент сопротивления.
Сила трения, отнесенная к единице объема [5]
(11)
Объемный коэффициент массопередачи можно определить по коэффициенту при спутном движении газа и струи рабочей жидкости:
(12)
где K – коэффициент массопередачи при спутном движении газовой и жидкой фаз.
Коэффициент сопротивления сf при спутном движении жидкостной и газовой струи определяется при числах Рейнольдса Re < 5∙105 по формуле Блазиуса [5]
(13)
Число Рейнольдса подсчитывается по формуле
(14)
где Z – расстояние от выходного сечения сопла до рассчитываемого. При числах Re больше 5∙105
(15)
Динамическая вязкость газов в области умеренных давлений не зависит от числа молекул в единице, то есть от давления [5] и является функцией температуры газа и может быть определена по формуле Сатерленда
(16)
где C – постоянная Сатерленда. Для умеренных температур можно принять
C = 184,5.
Значение динамической вязкости при умеренных давлениях и температуре 273,2 К
Окончательное выражение для определения динамической вязкости углекислого газа имеет вид:
(17)
Закономерности течения двухфазной среды на начальном участке в камере смешения описываются системой дифференциальных уравнений (4), (5), (6), (7). Параметры потоков рассчитываются в пределах каждого шага Δl. Граничными условиями для расчета параметров потоков являются: 
‒ начальная концентрация газа в рабочей жидкости; Pн – давление газа в приемной камере; tр – температура рабочей жидкости; tн – температура газа в приемной камере; u0 – коэффициент объемной подачи; m – значение основного геометрического параметра; Pр –давление подаваемой рабочей жидкости.
Расчет заканчивается в сечении начала распада струи. Значения параметров, получившиеся в результате расчета начального участка, являются входными данными для расчета параметров в области молочно-белой эмульсии.
Для расчета двухфазного потока в области молочно-белой эмульсии примем следующие упрощения:
1. Длина участка, на котором происходит распад струи в гомогенный поток, крайне незначительна и ею можно пренебречь.
2. Изменение структуры потока не сопровождается заметным растворением углекислого газа в рабочей жидкости.
Входными данными для расчета паромеров в зоне гомогенного потока являются данные последнего шага расчета начального участка.
На основании допущения об отсутствии массопередачи в сечении распада струи объемное газосодержание потока остается постоянным. Из уравнения сохранения импульса определим скорость двухфазного потока [5]:
(18)
где ωII–III – скорость двухфазного потока после добавления струи; 
– скорость соответственно потоков газа и рабочей жидкости в конце начального участка.
Уравнение неразрывности для двухфазного потока запишется в виде [5]:
(19)
Отсюда
(20)
Плотность рабочей жидкости ρр значительно больше плотности углекислого газа и можно записать [5]:
(21)
Отсюда
(22)
Массовая концентрация газовой фазы за сечением распада [5]:
(23)
По уравнениям (21), (22), (23) определяются плотность, объемное и массовое газосодержание в гомогенном потоке за сечением распада II–II.
Закон сохранения импульса напишется в виде [5]:
Дифференцируя это уравнение по dZ, получим [5]:
(24)
где Π = π⋅dк – параметр канала камеры смешения; mр, mг, – соответственно массовые расходы жидкой и газовой фаз; τω – касательное напряжение между двухфазным потоком и стенкой камеры вследствие сил трения.
Уравнение сохранения массы для гомогенного двухфазного потока в дифференциальной форме имеет вид [5]:
(25)
Дифференцируя уравнение (21) и подставляя полученное выражение в уравнения сохранения массы, получаем [5]:
(26)
Подставляя формулу (26) в (24), получаем уравнение изменения давления
(27)
Запишем соотношения масс газовой фаз [5]:
(28)
(29)
Поделив эти уравнения, получаем [5]:
(30)
Дифференцируя уравнения (30), получаем [5]:
(31)
Количество тепла, выделяющегося в результате растворения газа в воде, крайне незначительно, и процесс можно считать изотермическим, то есть подчиняющимся закону изотермического сжатия
(32)
В дифференциальном виде уравнение изотермического сжатия имеет вид:
(33)
Подставляя это выражение в формулу (31), получаем:
(34)
Скорость изменения массовой концентрации газа 
может быть определена из уравнения массопередачи
(35)
(36)
Учитывая, что, 
получаем:
(37)
Выражаем плотность газа из уравнения изотермы:
(38)
Подставляем это выражение в формулы (33) и (31)
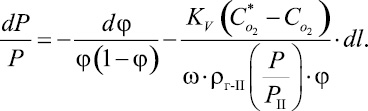(39)
Комбинируя это уравнение с уравнением (27), получаем зависимость давления от газосодержания в данном сечении:
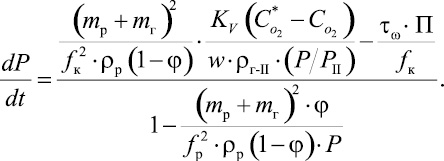(40)
Рассчитывая, что 
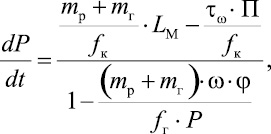(41)
где 
– множитель, учитывающий массопередачу в двухфазном потоке.
Таким образом, получаем систему дифференциальных уравнений, описывающих процессы гидродинамики и массопередачи в области молочно-белой эмульсии:
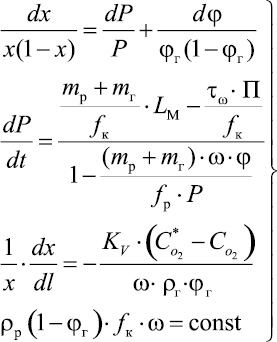(42)
Дополнительные уравнения:
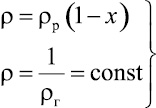
Касательное напряжение трения двухфазного потока о стенки камеры определятся по формуле [5]:
(43)
где
(44)
Полученная модель позволяет адекватно описать массообменные процессы в струйных аппаратах.
Рецензенты:
Глотова И.А., д.т.н., доцент, заведующая кафедрой технологии переработки животноводческой продукции Воронежского государственного агроуниверситета имени Императора Петра I, г. Воронеж;
Шашкин А.И., д.ф.-м.н., доцент, заведующий кафедрой дифференциальных уравнений, декан факультета прикладной математики, информатики и механики ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж.
Работа поступила в редакцию 21.12.2012.