Исследования струйных течений жидкостей, имеющих свободную поверхность, а также распада жидких струй на капли представляют собой актуальную научную проблему в виду наличия широкого спектра практических приложений данных явлений. Существует множество работ, посвященных изучению неустойчивости и распада струй [1–4]. Использование в подобных исследованиях магнитных жидкостей открывает новые возможности для изучения механизмов протекания данных явлений и позволяет обнаружить их новые аспекты благодаря возможности воздействовать внешним магнитным полем на жидкую струю. Ранее были выполнены некоторые работы, которые касались исследования струй магнитных жидкостей под действием параллельного струе магнитного поля [5, 6]. Было показано, что воздействие магнитного поля приводит к стабилизации такой струи. В данной работе исследуются особенности неустойчивости струи магнитной жидкости, находящейся под действием перпендикулярного ей внешнего магнитного поля.
Экспериментальные исследования и их результаты
Схема применявшейся экспериментальной установки представлена на рис. 1. Однородное магнитное поле формировалось с помощью катушек Гельмгольца 1, позволяющих получать горизонтально направленное однородное магнитное поле напряженностью до 110 Э. В пространство между катушками вводилась струя магнитной жидкости 2 так, что ось струи перпендикулярна вектору напряжённости магнитного поля. Скорость истечения струи регулировалась путём перемещения с помощью электродвигателя 5 поршня 3 вдоль резервуара с магнитной жидкостью 4. Диаметр струи составлял 2 мм, магнитная восприимчивость магнитной жидкости − 9,5. Поведение струи фиксировалось с помощью скоростной видеокамеры при частоте съёмки 300 кадров в секунду. На рис. 2 представлены мгновенные снимки струи в магнитном поле напряжённостью 60, 70, 80 и 90 Э.
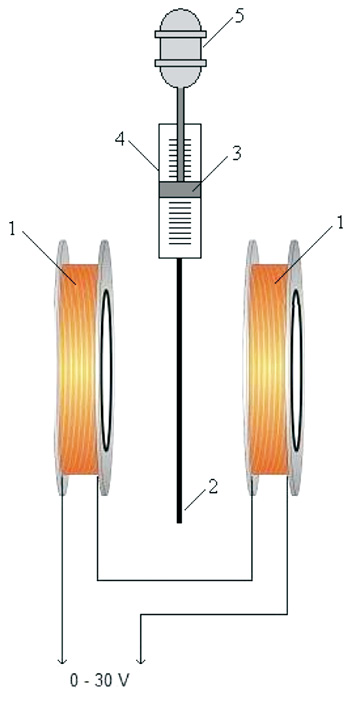
Рис. 1. Схема экспериментальной установки
В ходе проведения эксперимента установлено, что под действием магнитного поля вдоль поверхности струи развивается неустойчивость, приводящая к трансформации формы струи от цилиндрической к синусоидальной. При этом распад струи на капли происходит тем раньше, чем больше напряжённость магнитного поля и меньше скорость течения струи.
На рис. 3 и 4 графически представлены экспериментально полученные зависимости максимального отклонения и длины линейного участка струи от напряжённости магнитного поля при разных значениях скорости течения струи. Как следует из рисунков, с ростом скорости течения величина максимального отклонения струи от вертикали и длина линейного участка струи возрастают.
Анализ и обсуждение результатов
Будем рассматривать движение невязкой несжимаемой магнитной жидкости. Движение магнитной жидкости в магнитном поле описывается уравнением Навье–Стокса с добавлением в правой части магнитной силы, действующей на единицу объема жидкости:
![]() (1)
(1)
где Fv – сила вязкого трения, действующая на единицу объема жидкости. Учтем также уравнение разрывности и уравнения магнитного поля:
![]()
![]()
![]()
![]()
![]() (2)
(2)
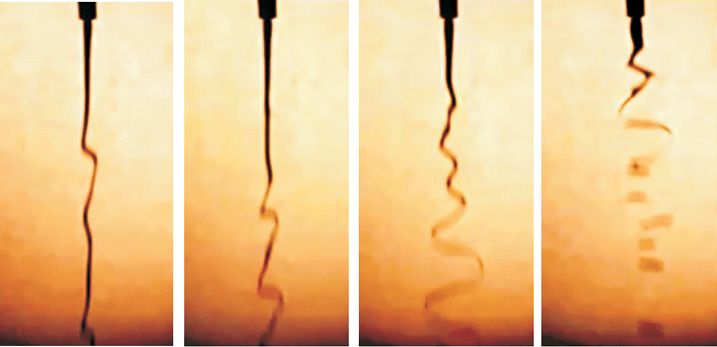
Рис. 2. Мгновенные фотографии струи в магнитном поле
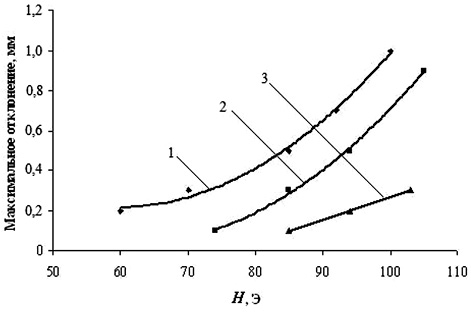
Рис. 3. Зависимость максимального отклонения струи от напряжённости магнитного поля при разной скорости течения струи: кривая 1 – 2,4 мм/с; кривая 2 – 4 мм/с; кривая 3 – 6 мм/с
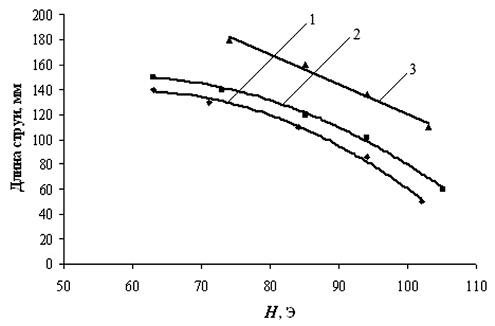
Рис. 4. Зависимость длины линейного участка струи от напряжённости магнитного поля при разной скорости течения струи: кривая 1 – 2,4 мм/с; кривая 2 – 4 мм/с; кривая 3 – 6 мм/с
Граничные условия для векторов поля имеют вид:
![]()
![]() (3)
(3)
Уравнение баланса давления на поверхности струи:
![]() (4)
(4)
где n – нормаль к поверхности; Tij – тензор напряжений; K – кривизна поверхности; σ – межфазное натяжение.
Будем рассматривать малые гармонические возмущения поверхности струи. Тогда, решая систему уравнений (1)–(4) в цилиндрических координатах, получим дисперсионное соотношение для возмущений в виде:
![]()
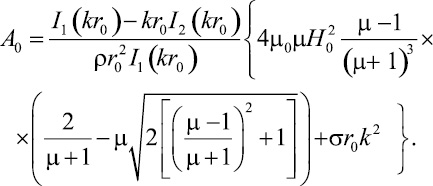 (5)
(5)
Волновое число неустойчивости k* можно найти из условия ∂w/∂k = 0. Подставляя k* в (5) найдем частоту возмущений w*. Длину струи можно оценить по выражению
![]() ,
,
где u0 – скорость струи. Соответствующий расчет приведен на рис. 5, где представлено сопоставление теоретических и экспериментальных данных.
Как видно, наблюдается удовлетворительное согласие экспериментальных и теоретических данных. Полученные результаты свидетельствуют о том, что воздействие перпендикулярного магнитного поля стимулирует развитие неустойчивости струи магнитной жикости.
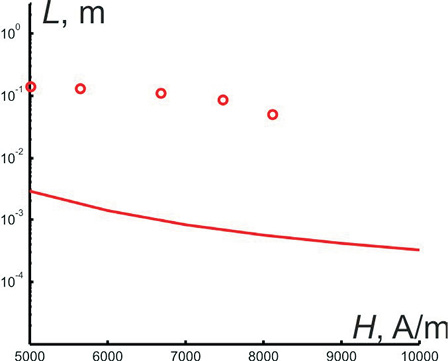
Рис. 5. Зависимость длинны струи от напряженности магнитного поля: линия – теоретический расчет, точки – экспериментальные данные
Работа выполнена при частичной поддержке гранта Президента РФ МК–6053.2012.2, а также при поддержке Министерства образования и науки РФ в рамках ведомственной аналитической научно-технической программы «Развитие научного потенциала высшей школы».
Рецензенты:
Ерин К.В., д.ф.-м.н., доцент, профессор кафедры общей физики СКФУ, г. Ставрополь;
Дерябин М.И., д.ф.-м.н., профессор кафедры общей физики СКФУ, г. Ставрополь.
Работа поступила в редакцию 22.11.2012.



