Полосковая линия в технике сверхвысоких частот − это плоскостная линия, канализирующая электромагнитные волны в воздушной или иной диэлектрической среде вдоль двух или нескольких проводников, имеющих форму тонких полосок и пластин. Такая структура может быть проанализирована с помощью различных методов: метода конформного отображения [6], метода конечных элементов (МКЭ), метода прямых (МП) [2], метода быстрого преобразования Фурье [8], метода моментов (ММ) [9], метода эквивалентных электродов (МЭЭ) [5], метода интегрального уравнения, метода обобщённого анализа спектральной области и др. Определение параметров полосковой линии важно для её правильного применения в печатных платах, для копланарных линий передачи, многослойных печатных плат, полосковых антенн, делителей мощности, фильтров и т.д.
Целью данной статьи является анализ полосковой линии, расположенной вертикально между двумя параллельными заземлёнными поверхностями, используя гибридный метод граничных элементов (ГМГЭ) [4] с соответствующей проверкой точности расчётов. Этот метод является комбинацией МЭЭ [10] и метода граничных элементов (МГЭ). МЭЭ-метод имеет некоторое сходство с ММ-методом и был успешно использован для расчёта многослойных сред и экранированной щелевой линии. В общем случае применение МЭЭ-метода зависит от функции Грина для решаемой задачи. Метод основан на комбинации аналитического метода функции Грина в замкнутой форме и численного метода, упрощающего решение задачи. В некоторых случаях нахождение функции Грина в замкнутой форме может быть достаточно трудным или даже невозможным. Заметим, что МЭЭ-метод не требует численного интегрирования. В ММ-методе численное интегрирование всегда присутствует. Это порождает некоторые проблемы в численном решении неэлементарных интегралов, имеющих единственную подинтегральную функцию.
Для того чтобы избежать численное интегрирование в МГЭ, можно использовать замену электродов произвольной формы на эквивалентные электроды (ЭЭ), и произвольной формы граничные поверхности между любыми двумя диэлектрическими слоями могут быть заменены дискретными эквивалентными общими зарядами на единицу длины, расположенными в пространстве. Для нахождения электрического скалярного потенциала зарядов, расположенных в свободном пространстве, можно использовать базовую функцию Грина. Это так называемый ГМГЭ-метод [4, 5, 10]. Метод основан на МЭЭ-методе и методе поточечного согласования (МПС) для потенциала идеальных электрически проводящих электродов и для нормальной компоненты электрического поля на граничной поверхности между двумя диэлектрическими слоями.
Для получения численных решений характеристик параметров полосковой линии, расположенной вертикально между двумя параллельными бесконечными заземлёнными поверхностями, была написана специальная компьютерная программа. Для анализа предполагалось, что в исследуемой полосковой линии распространяется квази-TEM волна. Для того чтобы проверить точность разработанного метода, были представлены численные результаты для всех примеров и проведено сравнение с результатами, полученными с помощью МКЭ-метода [3].
Теоретический подход
Поперечный разрез полосковой линии в многослойном диэлектрике между двумя заземлёнными поверхностями показан на рис. 1. В соответствии с ГМГЭ-методом электрод произвольной формы может быть заменён эквивалентными электродами, и произвольной формы граничная поверхность между любыми двумя диэлектрическими слоями может быть заменена на дискретную эквивалентную обобщённую линию зарядов, расположенную в промежуточном пространстве (рис. 2).
Техника дискретизации схожа с техникой хорошо известного метода моментов.
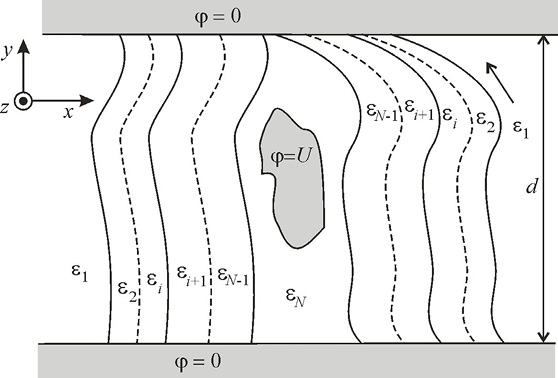
Рис. 1. Полосковая линия в многослойном диэлектрике
Поскольку свободных поверхностных зарядов не существует на границах раздела диэлектриков (свободные поверхностные заряды существуют только на полосковом проводнике (ПП), см. рис. 2), общие поверхностные заряды между диэлектрическими слоями равны связанным поверхностным зарядам.
Функция Грина линейного заряда, расположенного на высоте h параллельно двум бесконечным параллельным заземлённым поверхностям, записывается [6]:
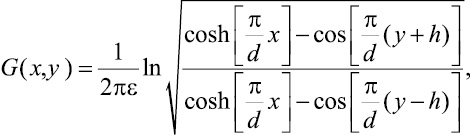(1)
где d – расстояние между двумя поверхностями.
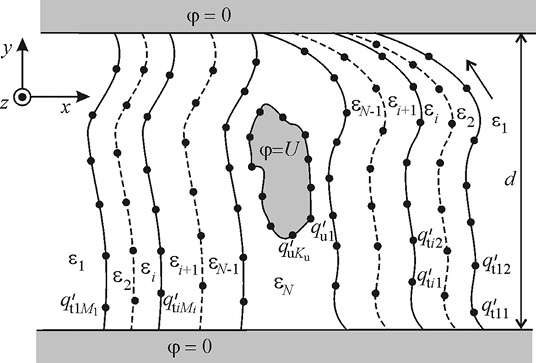
Рис. 2. Соответствующая ГМГЭ-методу модель
Используя эту функцию Грина, электрический скалярный потенциал для рассматриваемой системы на рис. 2 будет:
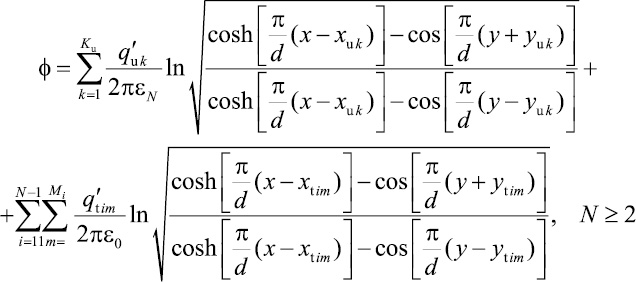(2)
и электрическое поле E = ‒grad(j), где Mi - число эквивалентных электродов на i-й границе поверхности между двумя слоями. В следующем примере общее число неизвестных Ntot запишем:
Связи между нормальными компонентами электрического поля и общим поверхностным зарядом запишем как:
(3)
где 
- единичный вектор нормали, ориентированный от слоя ei + 1 к слою ei.
Позиции соответствующих точек для потенциала ПП:
n = 1, ..., Ku; , k = 1, ..., Ku и 
, где dnk −это дельта функция Кронекера.
(4)
где aeuk соответствующие ЭЭ радиусы.
Граничные поверхности соответствующих точек для нормальных компонент электрического поля на i-й граничной поверхности:
и
i = 1, ..., N – 1, n = 1, ..., Mi и m = 1, ..., Mi, где 
−это ЭЭ радиусы.
Наша цель – получить систему линейных уравнений с неизвестными свободными зарядами ПП и общими зарядами на единицу длины на граничных поверхностях между диэлектрическими слоями. Используя МПС для потенциала проводника согласно (2) и МПС для нормальной компоненты электрического поля (3), можно определить неизвестные заряды. После решения системы линейных уравнений рассчитывается ёмкость на единицу длины полосковой линии по формуле:
(5)
Импеданс полосковой линии рассчитывается по формуле
,
где 
– эффективная диэлектрическая проницаемость, а Zc0 − это импеданс полосковой линии без диэлектрика (в свободном пространстве).
Для проверки полученных результатов расчёта величины импеданса был использован МКЭ-метод. Расхождение между расчётами по методам ГМГЭ и МКЭ определялось
(6)
Численные результаты и обсуждение
На рис. 3 показано поперечное сечение полосковой линии передачи, при этом полосок расположен вертикально между двумя бесконечными заземлёнными поверхностями и смещён от центра. Рассчитаем эффективную диэлектрическую проницаемость и импеданс линии, применяя ГМГЭ-метод. Результаты вычислений и требуемое время расчёта представлены в табл. 1 для er1 = 1, er2 = 1, s/d = 0,3, s1/s = 0,3, h/d = 0,2, w/d = 0,4 и t/w = 0,1. Достигнута очень хорошая сходимость результатов. Более того, максимальное время расчёта 170,5 с, соответствующее 1560 неизвестным, много меньше, чем 8 минут и несколько сотен тысяч конечных элементов, требуемых МКЭ для расчёта такой же геометрии.
Таблица 1
Сходимость и время расчётов
|
Ntot |
|
Zc[Ω] |
t(s) |
|
232 |
2,0721 |
65,254 |
6,0 |
|
342 |
2,0727 |
65,300 |
12,9 |
|
454 |
2,0730 |
65,327 |
22,9 |
|
564 |
2,0732 |
65,344 |
36,0 |
|
674 |
2,0733 |
65,355 |
51,1 |
|
786 |
2,0734 |
65,364 |
70,5 |
|
896 |
2,0734 |
65,371 |
91,2 |
|
1006 |
2,0735 |
65,376 |
117,2 |
|
1118 |
2,0735 |
65,381 |
141,7 |
|
1228 |
2,0736 |
65,385 |
170,5 |
Эквипотенциальные кривые и распределение поляризованных зарядов на единицу длины вдоль граничных поверхностей показано на рис. 4, 5 для параметров: er1 = 1, er2 = 3, s/d = 0,3, s1/s = 0,3, h/d = 0,2, w/d = 0,4 и t/w = 0,1. Значения эффективной диэлектрической проницаемости и импеданса, рассчитанные с помощью методов ГМГЭ и МКЭ, а также результаты вычисления отклонений представлены в табл. 2 и 3.
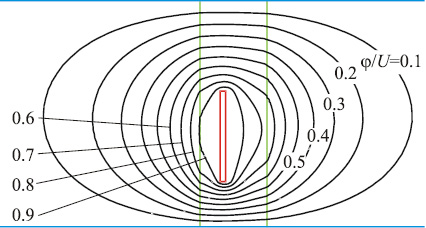
Рис. 3. Эквипотенциальные кривые
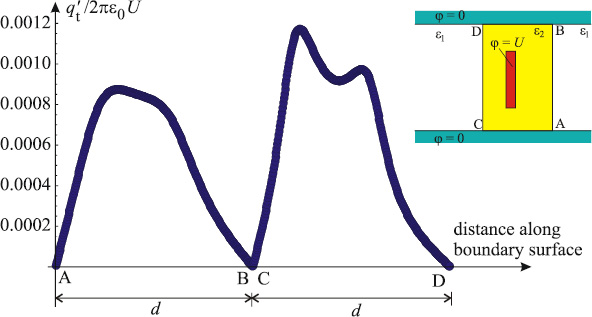
Рис. 4. Распределение поляризованных зарядов на единицу длины вдоль граничной поверхности
Таблица 2
Сравнение значений диэлектрической проницаемости и импеданса полосковой линии в зависимости от s1/s и h/d для er1 = 1, er2 = 3, s/d = 0,3, w/d = 0,4 и t/w = 0,05
|
|
|
ГМГЭ |
МКЭ |
||
|
|
Zc[Ω] |
|
Zc[Ω] |
||
|
0,3 |
0,1 |
2,2257 |
56,885 |
2,2262 |
56,830 |
|
0,2 |
2,0832 |
68,413 |
2,0836 |
68,347 |
|
|
0,3 |
2,0451 |
71,784 |
2,0455 |
71,712 |
|
|
0,4 |
2,0832 |
68,413 |
2,0836 |
68,347 |
|
|
0,5 |
2,2257 |
56,885 |
2,2262 |
56,830 |
|
|
0,4 |
0,1 |
2,2574 |
56,485 |
2,2578 |
56,432 |
|
0,2 |
2,1081 |
68,007 |
2,1086 |
67,943 |
|
|
0,3 |
2,0678 |
71,389 |
2,0682 |
71,315 |
|
|
0,4 |
2,1081 |
68,007 |
2,1086 |
67,943 |
|
|
0,5 |
2,2574 |
56,485 |
2,2578 |
56,432 |
|
|
0,5 |
0,1 |
2,2618 |
56,429 |
2,2623 |
56,376 |
|
0,2 |
2,1117 |
67,949 |
2,1122 |
67,882 |
|
|
0,3 |
2,0710 |
71,333 |
2,0715 |
71,263 |
|
|
0,4 |
2,1117 |
67,949 |
2,1122 |
67,882 |
|
|
0,5 |
2,2618 |
56,429 |
2,2623 |
56,376 |
|
Таблица 3
Сравнение значений диэлектрической проницаемости и импеданса полосковой линии в зависимости от w/d для er1 = 1, er2 = 3, s/d = 0,5, s1/s = 0,5, h/d = 0,2 и t/w = 0,05
|
|
ГМГЭ |
МКЭ |
δ[%] |
||
|
|
Zc[Ω] |
|
Zc[Ω] |
||
|
0,1 |
2,4347 |
106,735 |
2,4349 |
106,590 |
0,14 |
|
0,2 |
2,2754 |
87,673 |
2,2758 |
87,578 |
0,11 |
|
0,3 |
2,1744 |
76,550 |
2,1748 |
76,472 |
0,10 |
|
0,4 |
2,1117 |
67,949 |
2,1122 |
67,882 |
0,10 |
|
0,5 |
2,0814 |
60,099 |
2,0818 |
60,043 |
0,09 |
|
0,6 |
2,0902 |
51,821 |
2,0907 |
51,774 |
0,09 |
|
0,7 |
2,1758 |
41,243 |
2,1761 |
41,208 |
0,08 |
Полученные ГМГЭ-методом значения достаточно близки к тем, что получены МКЭ-методом. Наибольшее отклонение здесь всего 0,14 %.
Табл. 2 показывает, что при увеличении параметра h/d импеданс сначала увеличивается, а затем уменьшается. Наибольшее значение импеданса достигается в случае, когда центральный проводник полосковой линии расположен по центру между обкладками полосковой линии.
Заключение
ГМГЭ-метод применим для двумерного анализа полосковой линии. Рассчитывались два квазистатических параметра полосковой линии: эффективная диэлектрическая проницаемость и импеданс. Результаты расчётов сравнивались с результатами, полученными МКЭ. Получено хорошее соответствие в результатах вычислений: наибольшее отклонение в расчётах импеданса не превышало 0,55 %. Применение ГМГЭ очень эффективно и просто для двумерного анализа полосковых линий. Метод может быть успешно применён для случая произвольного числа проводников и произвольного числа диэлектрических слоёв. Метод позволяет проанализировать большое разнообразие очень сложных двумерных и трёхмерных задач, связанных с симметричной и несимметричной полосковыми линиями. Данную методику расчёта можно использовать при расчёте линии передачи с неоднородным или магнитоэлектрическим заполнением [1] и в дальнейшем применить для расчёта сложных СВЧ-устройств.
Работа выполнена при поддержке Министерства образования и науки Сербии в рамках проекта ТR 33008 и в рамках реализации Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Захаров А.Ю., д.ф.-м.н., профессор, заведующий секцией кафедры общей и экспериментальной физики ИЭИС НовГУ, г. Великий Новгород;
Корнышев Н.П., д.т.н., доцент, ведущий научный сотрудник НИИ ПТ «РАСТР», г. Великий Новгород.
Работа поступила в редакцию 21.12.2012.