Атомно-силовая микроскопия (АСМ) в настоящее время становится одним из самых перспективных методов изучения структурных особенностей макромолекул, поскольку позволяет получать изображения объектов с высоким разрешением, сопоставимым с уровнем рентгеноструктурного анализа, в условиях, при которых макромолекулы не подвергаются жесткой обработке и проявляют свою природную активность [1, 3–5]. Кроме того, атомно-силовая микроскопия дает возможность не только визуализировать объекты на молекулярном уровне, но и изучать свойства индивидуальных макромолекул: распределение поверхностных зарядов, подвижность отдельных участков, конформационные изменения в зависимости от условий, силу специфического взаимодействия между молекулами. С помощью атомно-силовой микроскопии можно наблюдать в реальном времени за сборкой макромолекулярных комплексов, распределением белков на поверхности клетки, особенностями внутриклеточного транспорта макромолекул и т.д.
Атомно-силовая микроскопия – вид зондовой микроскопии, в основе которого лежит силовое взаимодействие атомов. На расстоянии менее одного нанометра между атомами образца и атомом зонда (кантилевера) возникают силы отталкивания, а на больших расстояниях – силы притяжения. Идея устройства очень проста – кантилевер, перемещаясь относительно поверхности и реагируя на силовое взаимодействие, регистрирует ее рельеф. На основании прибора укреплен цилиндр, в котором находится сканер – пьезоэлектрическая керамика, изменяющая свои размеры при приложении электрического поля. В верхней части цилиндра крепится исследуемый образец, который сканер может перемещать в трех взаимно перпендикулярных направлениях. В горизонтальной плоскости образец сканируется по строкам: пройдя одну, он смещается на следующую строчку. Обычно таких строк 256, время движения вдоль строки может варьироваться примерно от 1 до 0,02 с, а длину строки в самом распространенном сканере можно выбрать от ~10 нм до ~10 мкм [2]. В зависимости от типа взаимодействия АСМ может работать в одном из нескольких режимов. Исследование биологических образцов происходит в основном в полуконтактном режиме, который отличается тем, что производит минимальное воздействие на образец и, соответственно, белковые структуры эритроцитов. В настоящей работе предлагается точный способ вычисления объема эритроцита по данным атомно-силовой микроскопии. Для сравнения предлагаемого способа расчета вначале необходимо рассмотреть классические способы расчета объема и метод Культера.
1. Классический способ расчета объёма эритроцитов
Средний объем эритроцитов или MCV (mean cell volume) вычисляется путем деления гематокритной величины 1 мм3 крови на число эритроцитов. Это более точный параметр, чем визуальная оценка размера эритроцитов (изменение диаметра эритроцита на 5 % приводит к изменению его объема на 15 %). Однако он не является достоверным при большом количестве эритроцитов с измененной формой (MCV может иметь нормальное значение при наличии у пациента одновременно выраженного макро- и микроцитоза). Следует помнить, что микросфероциты имеют диаметр меньше нормы, в то время как средний объем их чаще остается в норме, поэтому необходимо всегда производить микроскопию мазка крови.
На основании значения MCV различают анемии микроцитарные (дефицит железа, талассемия), нормоцитарные (апластическая анемия) и макроцитарные (В12- и фолиеводефицитные, апластические анемии). При этом единицами измерения являются фемтолитры (фл), очевидно, что 1 фл = 1 мкм3. В таблице приведены данные по изменению объема эритроцитов с возрастом, видно, что объем эритроцитов в основном меняется в диапазоне 70–100 фл. Поскольку референсные значения соответствуют средним значениям, для более глубокого понимания процессов, в которых принимают участие эритроциты, необходимы методики расчета, дающие точные значения объема для каждого эритроцита отдельно, что в дальнейшем позволит легко усреднить полученный результат.
2. Расчёт объема эритроцитов по данным атомно-силовой микроскопии
Для проведения расчета объема эритроцита по данным атомно-силовой микроскопии необходимо провести измерение скана поверхности мембраны (рис. 1) и затем произвести разрез скана эритроцита по диагонали с целью измерения его высотных геометрических характеристик. На рис. 2 показан график зависимости высоты стенки мембраны эритроцита от его продольной координаты вдоль диагонального разреза.
Референтные значения объёмов эритроцитов
|
Возраст, пол |
MCV, фл |
|
|
< 2 недель |
88–140 |
|
|
2–4,3 недели |
91–112 |
|
|
4,3–8,6 недель |
84–106 |
|
|
8,6 нед. – 4 мес. |
76–97 |
|
|
4–6 мес. |
68–85 |
|
|
6–9 мес. |
70–85 |
|
|
9–12 мес. |
71–84 |
|
|
1–5 лет |
73–85 |
|
|
5–10 лет |
75–87 |
|
|
10–12 лет |
76–94 |
|
|
12–15 лет |
женщины |
73–95 |
|
мужчины |
77–94 |
|
|
15–18 лет |
женщины |
78–98 |
|
мужчины |
79–95 |
|
|
18–45 лет |
женщины |
81–100 |
|
мужчины |
80–99 |
|
|
45–65 лет |
женщины |
81–101 |
|
мужчины |
81–101 |
|
|
> 65 лет |
женщины |
81–102 |
|
мужчины |
81–103 |
|
В условиях данной задачи, учитывая все проделанные приближения, можно пренебречь углом наклона эритроцита – на приведённом изображении (рис.2) тангенс этого угла равен ~0,02. Таким образом, полученная кривая разреза может быть представлена, как показано на рис. 2. Итоговый объём показанной фигуры можно представить в виде разности объёмов двух фигур – усеченного конуса и перевернутого конуса (см. рис. 2). Высоту усеченного конуса можно вычислить как среднее высот справа и слева эритроцита – l = (l1 + l2)/2, основания усеченного конуса равны R и r. Высота перевернутого конуса равна соответственно n = (n1 + n2)/2. Учитывая, что объем конуса равен V = Sh/3, где S = πR2/4 – площадь; h – высота конуса, можно вычислить объем эритроцита по формуле:
![]() (1)
(1)
где l1 и l2 – высота стенок эритроцита слева и справа соответственно; n1 и n2 – глубина впадины слева и справа соответственно, а R и r – радиусы основания и вершины эритроцита; коэффициент k – подгоночный параметр, который включает все константы и учитывает отклонение реального объема эритроцита от «идеальной» модели (см. рис. 2).
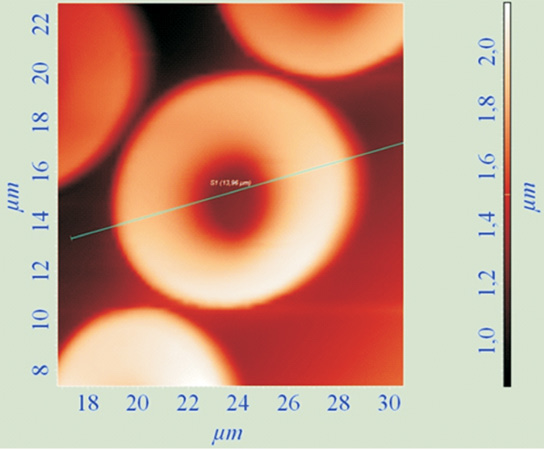
Рис. 1. Скан эритроцита ребенка (возраст 5 дней) размером 14×14 мкм2. Скан пересекает линия разреза, вдоль которой определяют геометрические характеристики эритроцита
Неопределённость в данную методику расчета вносят факторы поведения эритроцита после высушивания, степень погружения его в поверхность мазка, что учитывает коэффициент k, который определяется путём сравнения объёмов эритроцитов, полученных по формуле (1), с их значениями, полученными по другим методикам, например, по значениями из таблице или методом Культера. Необходимо отметить, что коэффициент определяется только один раз при калибровке методики, затем его значение остается неизменным для всех измерений. Для определения численного значения коэффициента k в формуле (1) был определен MCV у 27 человек методом Культера, затем проведен анализ данных атомно-силовой микроскопии и при сравнении полученных усредненных данных получили коэффициент k = 0,933. При этом значения объемов лежат в диапазоне 80–160 мкм3, что соответствует данным, приведенным в таблице. Анализу расчетных данных MCV по предложенной формуле будет посвящена следующая статья.
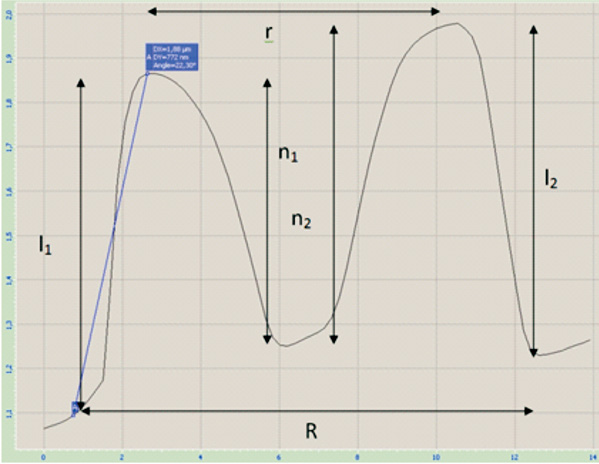
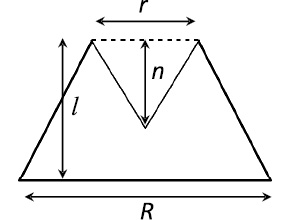
Рис. 2. График зависимости высоты стенки мембраны вдоль диагонального разреза скана эритроцита (слева) и геометрическая модель эритроцита (справа). Размеры на скане указаны в мкм. Изменение высоты происходит в диапазоне 1 мкм, координаты R в диапазоне 11 мкм
Заключение
Таким образом, в работе получено выражение для расчета объема эритроцитов по данным атомно-силовой микроскопии. Для измерения объема эритроцитов сначала проводят измерение скана мазка крови методом атомно-силовой микроскопии в полуконтактном режиме. Далее для каждого исследуемого эритроцита определяют геометрические характеристики морфологии, для чего проводят разрез эритроцита в поперечном сечении. В результате вычисляют диаметр эритроцита, его высоту, глубину и длину впадины. Предполагая, что форму эритроцита можно описать как разницу двух фигур – усеченного конуса и перевернутого конуса, была предложена формула определения объема эритроцитов.
Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы (соглашение № 14.B37.21.0228).
Рецензенты:
Лиманова Н.И., д.т.н., доцент, профессор ФГБОУ ВПО «Поволжский государственный университет телекоммуникаций и информатики», г. Самара;
Мельников Б.Ф., д.ф.-м.н., профессор кафедры прикладной математики и информатики ФГБОУ ВПО «Тольяттинский государственный университет», г. Тольятти.
Работа поступила в редакцию 26.11.2012.



