В отечественных нормативных документах основным критерием оценки предела огнестойкости по потере несущей способности является критическая температура бетона и арматуры, значение которой для тяжелых бетонов лежит в пределах 500 – 600 °С.
Однако в других альтернативных подходах в оценке предельного состояния капиллярно-пористого материала при интенсивном нагреве учитывается градиент температуры.
Следовательно, критерий критической температуры, используемый в стандартном методе оценки предела огнестойкости при воздействии «стандартного» пожара, каким-то образом должен быть сопряжен с критерием градиента температуры. Это обстоятельство мотивировало дальнейшие исследования авторов в области количественной оценки пожарного риска в части последствий воздействия высокоинтенсивного теплового излучения на элементы строительных конструкций.
Температурный и градиентный критерии огнестойкости
Проблема теплового удара является одной из центральных в термомеханике [3]. Проводимые исследования для решения данной проблемы с использованием моделей динамической термоупругости получили широкое развитие при изучении закономерностей термонапряженного состояния в изотропных и анизотропных упругих телах. Применительно к одностороннему равномерному нагреву элементов конструкций можно записать известное уравнение Даниловской [1, 2]
(1)
здесь V – скорость распространения упругой волны, которая определяется из соотношения
(2)
где λ и μ – постоянные Ламе; ρ – плотность материала; S – постоянная, выражается через коэффициент линейного температурного расширения материала α в виде
S = α(2μ + 3λ). (3)
Граничные условия
(4)
Возникающее вследствие неравномерного нагрева материала напряжение U(x, τ), входящее в уравнение (1), удовлетворяет начальному условию
(5)
граничному условию
(6)
Нахождение аналитических решений такого рода динамических задач (даже в линейной постановке) связано с большими техническими трудностями и является длительным процессом. Таким образом, как видно из уравнения (1), в критериях разрушения бетона должен учитываться градиент температуры.
Обоснование комплексного критерия разрушения
При обосновании комплексного критерия огнестойкости, учитывающего влияние критической температуры, градиента температуры и теплофизических свойств бетона, авторами проанализированы постановка и решение различных краевых задач нестационарной теплопроводности.
В реализации предлагаемого подхода анализируются две краевые задачи.
В первой – рассматривается решение классической задачи Стефана по промерзанию грунта [5]
(7)
где T0 – температура талой воды; ξ– координата подвижной границы при постоянной температуре замерзания; Tз, B – постоянный коэффициент;α– коэффициент температуропроводности; τ – время.
Применительно к расчету огнестойкости предлагается задачу Стефана предельно упростить за счет исключения теплоты фазового перехода. При этом градиент температуры с обеих сторон подвижной границы становится одинаковым, и за ξ принимается граница распространения критической температуры Tкр, за Th – температура бетона на расстоянии шага численного интегрирования уравнения энергии hx от подвижной границы. Тогда
(8)
Далее закон Фурье для плотности теплового потока записывается в виде:
(9)
где |gradT|x – модуль проекции градиента температуры на координатную ось Ох; λбет ‒ теплопроводность бетона.
Разностный аналог модуля градиента температуры на подвижной границе можно записать в виде
(10)
После умножения обеих частей уравнения (10) на 
и несложных преобразований получено
(11)
Деление (11) на Tкр позволяет получить
(12)
Перегруппировка переменных в (12) позволяет получить
(13)
Принимается 
. Тогда
(14)
Кроме того, в диапазоне изменения параметровξ, α, τ зависимость функции Крампа от аргумента близка к линейной. Тогда
(15)
Во второй краевой [4] задаче в начальный момент времени τ = 0 все точки полуограниченного твердого тела имеют одинаковую начальную температуру T0 и задан произвольный закон изменения теплового потока от времени на границе тела. В этой задаче имеется частный случай, когда изменение теплового потока обеспечивает постоянство температуры на поверхности
(16)
В нашем случае за T0 принимается критическая температура Tкр
(17)
Из (17) следует
(18)
Принимается также, что
(19)
получается
(20)
С использованием критериев (15) и (20) были обработаны данные вычислительного эксперимента для различных сценариев пожаров, включая стандартный, горение углеводородов и термита. Результаты представлены на рис. 1 и 2.
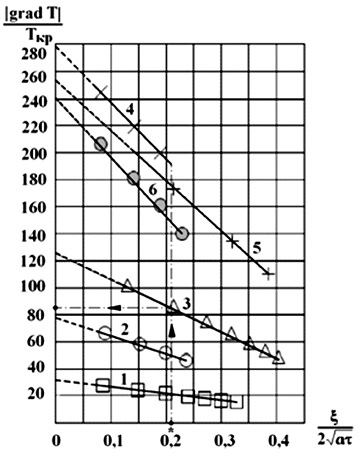
Рис. 1. Зависимость приведенного градиента температуры от безразмерной координаты подвижной границы:1 – стандартный пожар; 2 – пожар разлития; 3 – факельное горение; 4 – огненный шар; 5 – вспышка; 6 – термит; * – критическое значение аргумента
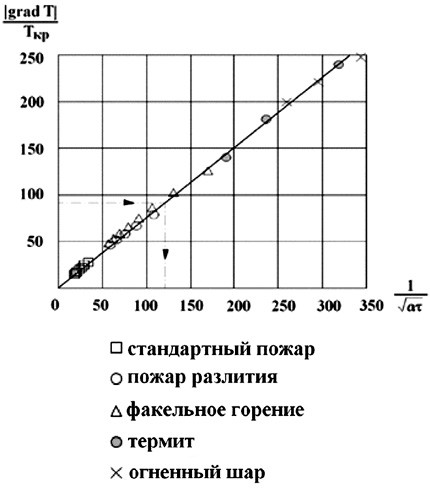
Рис. 2. Зависимость приведенного градиента температуры от комплекса 
Как видно из рис. 1, приведенный градиент температуры линейно зависит от безразмерного комплекса 
для каждого вида пожара с различными угловыми коэффициентами, а из рис. 2 – линейная зависимость приведенного коэффициента от 
является единой для всех видов пожаров с угловым коэффициентом K2 = 0,75.
Полученные зависимости могут быть использованы для прогнозирования предела огнестойкости элементов ж/б конструкций.
Как видно из результатов математического моделирования, время достижения максимальной температуры в приповерхностном слое бетона зависит от скорости горения ПС. На рис. 3 а скорость горения составляет 3,6 мм/с, на рис. 3 b – 2 мм/с.
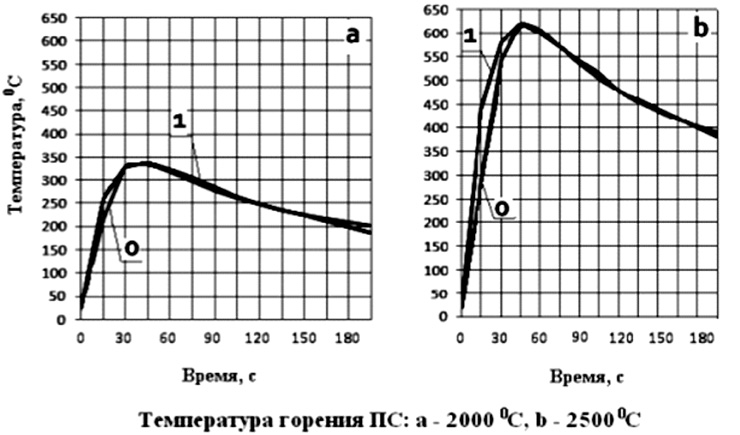
Рис. 3. Результаты моделирования высокоинтенсивного нагрева бетона: 0 – эксперимент, 1 – модель нагрева пиросоставом
Анализ результатов эксперимента нагрева бетона с использованием ПС показывает, что после сгорания ПС образование магистральных трещин на поверхности бетонных блоков и, как следствие снижение прочности наступает через 3–8 минут у образцов, критическая температура которых достигает значения 600 °С на глубине 2 мм от поверхности высокоинтенсивного нагрева и выше. При этом у образцов базового состава, у которого максимальная температура сохраняется более длительное время, протяженность трещин и ширина раскрытия являются максимальными, как это видно на рис. 4 и 5.
Рис. 4
Рис. 5
Выводы
1. Обоснован градиентно-температурный критерий разрушения бетона при высокоинтенсивном нагреве от продуктов горения углеводородного топлива.
2. Предложен вычислительный алгоритм предпроектной оценки огнестойкости элементов железобетонных конструкций при высокоинтенсивном нагреве.
Рецензенты:
Лашков В.А., д.т.н., профессор, зав. кафедрой «Машиноведение», КНИТУ, г. Казань;
Николаев А.Н., д.т.н., профессор, зав. кафедрой «Оборудование пищевых производств», КНИТУ, г. Казань.
Работа поступила в редакцию 07.09.2012.