Для того чтобы вибрационный полет стал реальным, сила сопротивления корпуса или крыла должна быть очень большой, а отношение максимальной величины силы аэродинамического сопротивления, соответствующей движению крыла вниз, к минимальной, когда крыло движется вверх, должно быть значительным [1]. Наиболее простым и очевидным решением обеих проблем является вращение крыла. При вертикальном положении крыла сила сопротивления минимальна, при горизонтальном – максимальна, а большое значение силы аэродинамического сопротивления возникает при быстром вращении крыла. Совершенно очевидно, что простое вращение плоского крыла не может создать отличную от нуля подъемную силу, отождествляемую с так называемой вибрационной силой [2]. Дело в том, что средняя за период вращения сила сопротивления, действующая на плоское крыло, равна нулю. Для того, чтобы подъемная сила вращающегося крыла не равнялась нулю, усреднение вертикальной составляющей силы сопротивления должно проводиться не за весь период, а только за часть его. Технически это может быть достигнуто применением экрана, в той или иной мере ограничивающего взаимодействие крыла с окружающим воздухом. Второй способ решить указанную выше двойную проблему состоит в дополнительном повороте крыла синхронно с основным вращением. Таких конструкций, понятно, предложить можно очень много. Заслуживают внимания решения, отличающиеся простой, возможностью получения больших скоростей поворота крыла и, разумеется, надежностью. Этого можно достичь при так называемом эпициклоидном вращении плоскости. Эпициклоидой называется траектория, описываемая точкой, а в данном случае элементом поверхности dS, отстоящим на расстоянии r от центра круга D, катящегося без скольжения по окружности A и находящегося вне этой окружности [3].
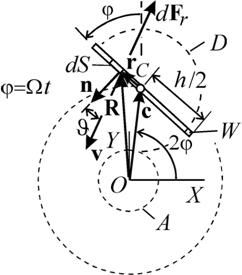
Рис. 1. Эпициклоидное крыло.
Положение элемента площади dS задается вектором
.
При повороте крыла на угол j=Wt ось вращения C ведомого диск D поворачивается на угол 2j=2Wt. Поэтому
, (1)
и скорость этого элемента поверхности относительно среды
, (2)
где ex и ey – единичные векторы вдоль осей X и Y, соответственно. В дальнейшем понадобится также модуль скорости:
. (3)
Сила сопротивления dF, действующая на этот элемент площади пропорциональна квадрату скорости, величине площади, антипараллельна скорости и пропорциональна косинусу угла J между направлением нормали n и скорости этого элемента площади относительно воздуха [4]:
, (4)
где C – коэффициент аэродинамического сопротивления, r - плотность воздуха. Последнее выражение удобно переписать через векторное произведение v и r :
. (5)
Компоненты векторов v и r можно найти в выражениях (1) и (2), после этого вертикальная составляющая сила сопротивления приобретает вид:
. (6)
Для того, чтобы вычислить подъемную силу, это выражение нужно проинтегрировать по площади крыла и усреднить по периоду T=2p/W:
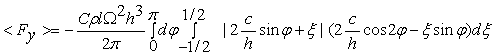. (7)
При этом учитывается, что в течение второй половины периода создается точно такое же значение подъемной силы, как и в течение первой. Следует обратить внимание, что интеграл зависит только от c/h. Это дает возможность изучить зависимость величины 6p<Fy>/CrlW2h3 от c/h. Результаты численного интегрирования (7) целесообразно сравнить с подъемной силой, создаваемой плоским крылом при поперечном вращении (0<r<h;c=0) с полупериодным экранированием:
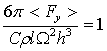. (8)
Эти результаты представлены на рис. 2. Интересно, что при больших значениях c/h результаты численного интегрирования практически совпадают с подъемной силой
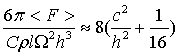, (9)
полученной приближенным интегрированием в предположении, что |2csinj+r|»2csinj+r. При c/h>0.3 эпициклоидное крыло создает большую силу по сравнению с поперечно вращающимся крылом. Для того чтобы выяснить, насколько эффективно эпициклоидное крыло, этого мало. Надо еще разобраться с энергией, затрачиваемой на тот и другой способ вращения плоского крыла.
Работа, совершаемая силой аэродинамического сопротивления, при перемещении dR элемента поверхности крыла dS есть ничто иное, как
. (10)
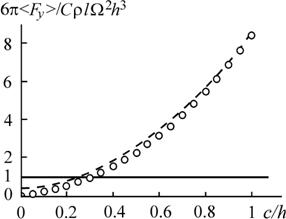
Рис. 2. Подъемная сила двух способов вращения плоского крыла. Точки – результаты численного интегрирования. Сплошная прямая – расчет (8) для поперечного вращения, штриховая кривая – зависимость (9).
Рис. 3. Потери энергии при эпициклоидном (точки) и поперечном (сплошная прямая) вращении.
Интерес, разумеется, представляет мощность, затрачиваемая летательным аппаратом, на осуществление вращения в поле диссипативных сил:
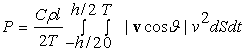, (11)
где модуль скорости v определяется выражением (3), а модуль проекции скорости на направлении нормали вычислен (6) и равен W|2csinj+r|. Поэтому
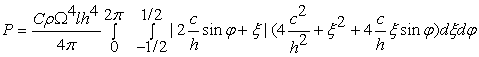, (12)
а для поперечного вращения крыла потребляемая мощность равна
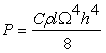. (14)
Как и прежде интеграл (12) зависит только от отношения c/h. Это дает возможность результаты численного интегрирования (12) представить в виде одной единственной зависимости безразмерной величины 8P/(CrW4lh4) от c/h (рис. 3). Для поперечного вращения эта величина равна единице. Получился несколько неожиданный результат. Ожидалось, что эпициклоидное крыло будет энергетически более выгодным, а оказалось, что потери энергии на такое вращение меньше потерь энергии при поперечном вращении только в той области, где создаваемая эпициклоидным вращением подъемная сила сравнительно мала. Выбор того или иного способа вращения, судя по всему, может быть сделан исходя из каких-то других соображений.
СПИСОК ЛИТЕРАТУРЫ:
1. Герасимов С.А., Удалова Е.С. Критический режим вибрационного полета с квадратичным сопротивлением движению. // Техника и технология. 2005. № 1. С. 17-20.
2. Блехман И.И. О вибрационной механике и вибрационной технике. – М.: Наука. 1988. – 208 с.
3. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука. 1977. С. 75.
4. Стрелков С.П. Механика. – М.: Наука. 1975. 560 с.