В работе [4] доказана теорема, определяющая один из путей приближенного компьютерного моделирования эмоций человека и животных. Тем не менее психологические свойства высших живых существ настолько запутаны и неоднозначны, что мы математически опишем эмоциональное поведение роботов, отвлекаясь от реальных эмоций человека и, в то же время, аккумулируя при этом основные психологические законы его деятельности.
Модели уровней воспитательного процесса
В работах [5, 6] предложены математические определения эмоции робота, воспитания и уровней воспитания, относительной невосприимчивости робота к воспитанию, основанные на гипотезе грузинского психолога Д.Н. Узнадзе [1, 2, 7].
Определение 1. Эмоции, влекущие равные элементарные воспитания, назовем равноценными.
Определение 2. Забывчивого робота, у которого все коэффициенты памяти, соответствующие конечному моменту времени каждой эмоции, равны и постоянны, назовем равномерно забывчивым.
В работе [5] доказано, что для функции воспитания равномернозабывчивого робота R на положительных равноценных эмоциях с течением времени t наступает пресыщение1 (рис. 1).
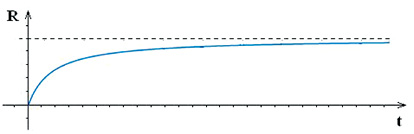
Рис. 1. Пресыщение функции воспитания робота
Применение гипотезы академика Узнадзе в теории Эмоциональных роботов помогло решить проблему пресыщения воспитания робота [5]. Решение проиллюстрировано на рис. 2.
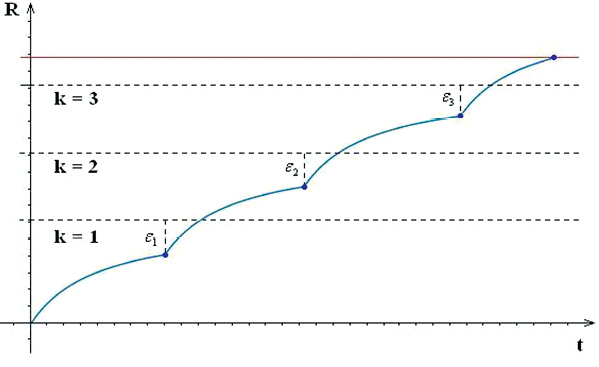
Рис. 2. Решение проблемы пресыщения воспитания робота
Определение 3. Уровнем воспитания робота k назовем количество смен эталонных эмоций (установок) робота к текущему моменту времени воспитательного процесса.
Величины εk, где 
, назовем отклонениями значения воспитания робота на уровне k от предела воспитания робота на этом уровне. Будем рассматривать случай, когда ε1 = ε2 = ... = εn = ε .
Отметим, что при компьютерной реализации алгоритма Д.Н. Узнадзе в качестве одного из входных параметров целесообразнее использовать относительную невосприимчивость к воспитанию α, смысл которой определяется формулой
,
т.е. величина α показывает часть предельного воспитания [6], при достижении которой происходит переход от первого уровня итогового воспитания ко второму уровню. Очевидна справедливость двойного неравенства 0 < α < 1.
В работе [5] показано, что при выполнении условия α = θ справедлива формула
,
при α < θ верно соотношение
,
при α > θ справедливо равенство
.
Модели долговременной памяти робота
В зависимости от длительности хранения информации можно выделить кратковременную и долговременную память.
«Кратковременная память представляет собой способ хранения информации в течение короткого промежутка времени. Длительность удержания мнемических следов здесь не превышает нескольких десятков секунд, в среднем около 20 (без повторения). В кратковременной памяти сохраняется не полный, а лишь обобщенный образ воспринятого, его наиболее существенные элементы. Эта память работает без предварительной сознательной установки на запоминание, но зато с установкой на последующее воспроизведение материала... Долговременная – это память, способная хранить информацию в течение практически неограниченного срока. Информация, попавшая в хранилища долговременной памяти, может воспроизводиться человеком сколько угодно раз без утраты. Более того, многократное и систематическое воспроизведение данной информации только упрочивает ее следы в долговременной памяти» [3].
Проецируя психологические свойства человека на роботов, будем говорить, что коэффициенты памяти θi, описанные в работах [4–6], характеризуют кратковременную память робота.
Определение 4. Коэффициентом долговременной памяти робота 
, присущей воспитательному уровню с порядковым номером k, назовем величину, удовлетворяющую соотношению
(1)
где R[k], R[k–1] являются воспитаниями робота на уровнях k и k – 1 соответственно.
Легко показать, что для равномерно забывчивого робота с равноценными эмоциями (в терминах относительной невосприимчивости робота к воспитанию α) величина описывается формулой
(2)
Таким образом, соотношение (2) определяет связь между долговременной памятью, описываемой коэффициентом 
, и кратковременной памятью, описываемой коэффициентом θ, равномерно забывчивого робота с равноценными эмоциями.
Опишем некоторые свойства этой связи.
Свойство 1. 
.
Свойство 2. При невосприимчивости робота к воспитанию α, равной нулю, справедливо соотношение 
Доказательства обоих свойств с очевидностью следуют из формулы (2).
После небольших преобразований получаем:
(3)
Отметим, что исходя из здравого смысла, коэффициент долговременной памяти робота 
. Напомним, что для формулы (3) должны выполняться условия:
0 < θ < 1, 0 < α < 1, k ∈ N. (4)
Рассмотрим несколько графических изображений функции 
, построенные в пакете Mathematica 7.01, варьируя k (рис. 3, 4, 5).
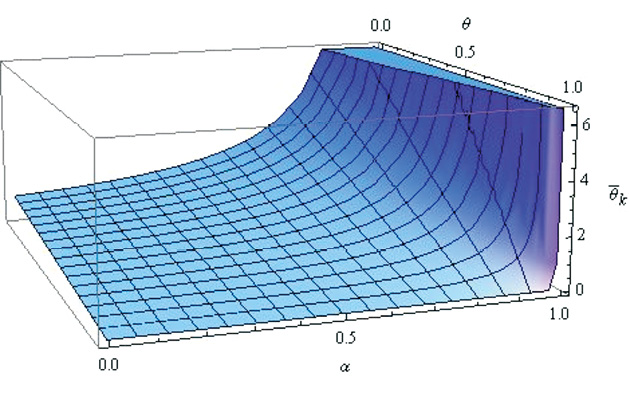
Рис. 3. Функция долговременной памяти при k = 1
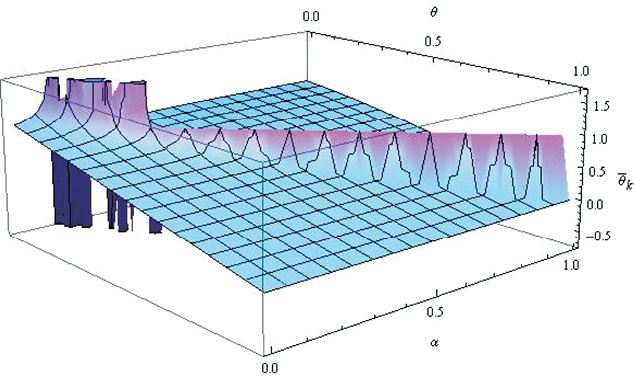
Рис. 4. Функция долговременной памяти при k = 8
Свойство 1 функции 
демонстрирует (рис. 5).
Исследуем, при каких величинах θ, α, k из области допустимых значений (4), коэффициент долговременной памяти 
принадлежит полуинтервалу [0,1):
(5)
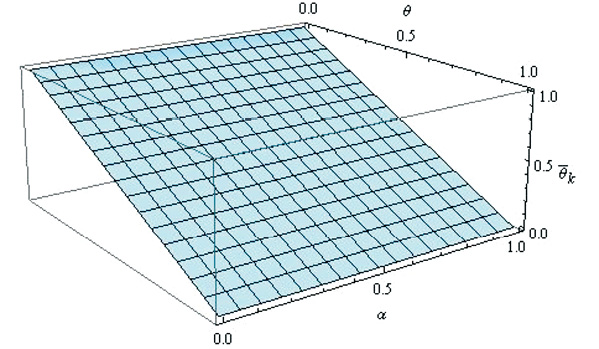
Рис. 5. Функция долговременной памяти при k = 2000
Рассмотрим 3 случая.
1 случай.
(6)
После несложных преобразований получаем, что 
, при 
Обратим внимание на то, что в предложенной модели α = const не зависит от θ и k. Поэтому в рамках этой модели случай 1 учитываться не будет.
2 случай.
(7)
После решения неравенства (7) получаем следующую совокупность решений:
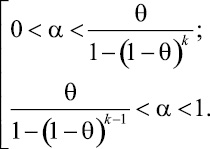(8)
3 случай.
(9)
В результате решения неравенства (9) получаем совокупность решений:
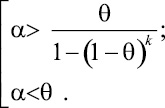(10)
Таким образом, двойное неравенство 
справедливо при выполнении условий
(11)
Заключение
Таким образом, в настоящей статье на основе гипотезы грузинского психолога Д.Н. Узнадзе об установках вводится математически формализованное понятие долговременной памяти робота, что позволяет проводить качественный и численный анализ взаимосвязи коэффициентов долговременной и кратковременной памяти робота и его неспособности к воспитанию.
Рецензенты:
Тарунин Е.Л., д.ф.-м.н., профессор кафедры прикладной математики и информатики Пермского государственного национального исследовательского университета, г. Пермь;
Ясницкий Л.Н., д.т.н., профессор, заведующий кафедрой прикладной информатики и искусственного интеллекта Пермского государственного гуманитарно-педагогического университета, г Пермь.
Криштоп В.В., д.ф.-м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Kwangwoon University, Seoul, Korea.
Работа поступила в редакцию 12.12.2012.
1 Выражение «функция имеет пресыщение» вводится в теории Эмоциональных роботов и эквивалентно выражению «функция монотонна и ограничена» в классической математике.