Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Общеизвестны трудности решения задачи построения уравнений регрессии в условиях, когда среди совокупности предположительно влияющих на некоторый показатель факторов имеются неуправляемые либо инерционные параметры. Получаемый при этом план полного факторного эксперимента содержит ортогональную часть матрицы исходных данных, включающую малоинерционные параметры, и другую часть матрицы – не ортогональную, включающую инерционные либо неуправляемые параметры. Это затрудняет проведение масштабирования (нормировку) реальных значений факторов к интервалу[–1, 1]. Вследствие этого при обработке данных проведенного активно-пассивного эксперимента (АПЭ) с использованием методов регрессионного анализа коэффициенты полученного уравнения регрессии оказываются корреляционно связанными между собой. Этого можно избежать, если использовать ортогонализацию плана и обеспечить за счет этого условие ортогональности матрицы независимых переменных [1, 2]. Определенный недостаток существующей методики [6] состоит в использовании предположения о том, что оцениваемые в ходе эксперимента значения функции отклика – случайные величины с известной дисперсией. Однако в условиях ограниченного объема данных и невозможности проведения повторных опытов эта гипотеза не проверяема. Кроме того, в ходе вычислительных экспериментов не исключаются случаи, когда при нахождении решения относительно неизвестных коэффициентов модели одно или несколько уравнений системы вырождаются, обращаясь в тождество. Вследствие чего соответствующие коэффициенты из этой неопределенной системы определить невозможно.

В данной работе рассмотрен метод определения линейного уравнения регрессии с использованием поэтапной искусственной ортогонализации активно-пассивного эксперимента.

Допустим, что имеем n входных параметров, причем X1,…, Xp из них – малоинерционные управляемые параметры, Xp + 1,…, Xm – инерционные управляемые и Xm + 1,…, Xn – неуправляемые параметры. Тогда преобразование исходных данных матрицы планирования осуществим по формуле:

где Xij – значение j-го параметра в i-м опыте;

Предположим, что искомая зависимость является линейной вида:

Y = Z0 + b1Z1 + … + bpZp + bp + 1Zp + 1 ++ … + bmZm + bm + 1Zm + 1 + … + bnZn.

Тогда соответствующую систему уравнений можно записать в виде:

(1)

где i = 1, …, N; t = 1, …, p; k = p + 1,…,m; l = m + 1,…,n; rit = ±1.

В матрице системы (1) столбцы, соответствующие малоинерционным парамет­рам, т.е. столбцы с t = 1, …, p, – ортогональные, остальные же столбцы с p + 1 по n – неортогональные. Данную систему уравнений (1) для определения коэффициентов регрессии независимо друг от друга можно решить, например, методом ортогонализации столбцов [2], т.е. столбцы, начиная с p + 1 по n, надо доортогонализировать. При этом решение системы в матричном виде имеет вид:

В = T–1D–1RTR,

где T – треугольная матрица; R – ортогональная матрица; RT – ортогональная транспонированная матрица; D = RTR – диагональная матрица.

Во всей процедуре решения системы этим способом особенно трудоемким является этап ортогонализации матрицы, причем с увеличением числа неортогональных столбцов трудоемкость вычисления резко возрастает. В случае, когда матрица полностью ортогональна, причем уровни варьирования параметров равны ±1, треугольная матрица T и обратная ей матрица T–1 превращаются в единичную, и выражение для определения коэффициентов регрессии сводится к виду:

где rij – уровни варьирования параметров, равные ±1; Yi – значение выходного параметра в i-м опыте; N – количество опытов, равное либо полному факторному эксперименту (ПФЭ), либо регулярной реплике от ПФЭ.

Для искусственной ортогонализации столбцов инерционных управляемых и неуправляемых переменных сделаем к ним добавки соответственно Δαik и Δβil таким образом, чтобы сумма (αik + ∆αik) ∆αik) и (βil + ∆βil)∆βil равнялись +1 или –1 в зависимости от того, какие уровни стоят в столбцах ортогональной матрицы планирования (выбранные, например из [1]), к которой сводится исходная матрица. А чтобы система (1) не нарушилась, необходимо и к правой ее части прибавить соответствующие добавки и . Тогда система (1) примет вид:

(2)

Матрица, соответствующая левой части системы (2), является полностью ортогональной, поэтому для решения системы можно использовать формулу:

(3)

где Ui – соответственно вся правая часть системы (2).

В результате получаем систему уравнений относительно известных bp + 1 ,…, bn:

(4)

где t = p + 1, …, n.

Опреде­лив из (4) коэффициенты bp + 1 ,…, bn и подставив их в правую часть (2), найдем далее коэффициенты b0, b1, …, bp по формуле (3).

Полученная система (4) всегда совместна, так как в матрице системы (2) столбцы ортогональны и, следовательно, линейно независимы. Однако в ходе вычислительных экспериментов было обнаружено, что в некоторых случаях в системе уравнений относительно неизвестных коэффициентов модели (4) одно или несколько уравнений вырождаются, обращаясь в тождество. Вследствие чего соответствующие коэффициенты из этой неопределенной системы определить невозможно. Методика, изложенная в работе [3], не дает прямых рекомендаций по разрешению этой ситуации с исходными (заданными) экспериментальными данными. В связи с этим в данной работе предлагается правило устранения неопределенности системы. Для этого достаточно в исследуемой матрице планирования соответствующие столбцы заменить на другие, не нарушающие ортогональности всей матрицы, и затем исходную матрицу свести к последней описанным в [3] способом.

Рассмотрим применение изложенного метода для построения зависимостей между показателями качества переходного процесса и параметрами нейросетевой модели (НСМ), используемой в составе регулятора системы управления температурой в биореакторе микробиологического синтеза. В качестве регулятора использован регулятор с предсказанием, реализованный в пакете Neural Network Toolbox и использующий модель управляемого объекта в виде нейронной сети (НС) для того, чтобы предсказывать его будущее поведение [5]. Основной принцип рассматриваемого регулятора состоит в нахождении на каждом шаге дискретности i такой последовательности управляющих воздействий, û[i]…û[i + j],которая, будучи приложена к объекту, обеспечит максимальное совпадение последовательности прогнозируемых значений выхода объекта ŷ[i] … ŷ[i + j] c последовательностью его желаемых значений g[i] … g[i + j]. Эта задача решается путем численной минимизации целевого функционала, одна из распространенных форм которого имеет вид [4]:

(5)

где û – управляющий сигнал; g, ŷ – эталонная и истинная реакция модели управляемого объекта; N1, N2 – константы, в пределах которых вычисляются ошибка слежения и мощность управляющего сигналов; ρ – коэффициент, определяющий вклад, вносимый мощностью управления в критерий качества.

В качестве НСМ используем модель двухслойного персептрона, для которой необходимо назначить количество нейронов, значения весов и смещений, которые минимизируют ошибку решения. Это достигается с помощью процедуры обучения. На рис. 1 и 2 представлены полученные зависимости при обучении НС. Из рис. 1, 2 видно, что при увеличении количества нейронов в слоях НС свыше 11 ошибка обучения увеличивается, а с увеличением числа циклов обучения свыше 50 ошибка обучения снижается незначительно при всех вышеприведенных методах обучения НС. Т.е. НС качественно работает с числовыми данными, находящимися в некотором ограниченном диапазоне. Наиболее быстро «обучаемой» НС является двухслойный персептрон, устанавливающий параметры весов методом Левенберга-Марквардта.

На основе полученной зависимости ошибки обучения от числа нейронов в скрытом слое НС (рис. 1) и числа циклов обучения с различными алгоритмами обу­чения (рис. 2) были назначены факторы варьирования в эксперименте. Поскольку зависимости нелинейны, а показатели качества переходного процесса, как правило, противоречивы, то значения факторов варьирования могут выходить за пределы этого диапазона и, как следствие, уровни факторов варьирования оказываются несимметричны, а матрица планирования оказывается неортогональной.

Рассмотрим построение модели влияния количества нейронов в скрытом слое (Nc), значения верхнего предела функционала (N2), внутри которого вычисляется мощность управления, количества нейронов в выходном слое (Nв) на величину перерегулирования в системе. Исходная матрица планирования проведенного активно-пассивного эксперимента с одной управляемой Nc и двумя контролируемыми переменными N2, Nв, имеет вид, представленный в табл. 1. Предположим, что зависимость между факторами x1, x2, x3 (Nc, N2, Nв) и перерегулированием у в нейросетевой системе управления может быть представлена в виде, линейном относительно искомых коэффициентов b0, b1, b2, b3:

у = b0 + b1x1 + b2x2 + b3x3, (6)

где b0, b1, b2, b3 – коэффициенты регрессии.

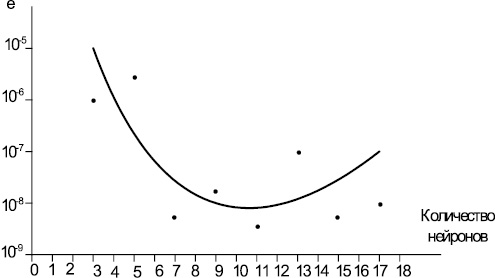
Рис. 1. Зависимость ошибки обучения от числа нейронов в скрытом слое НС

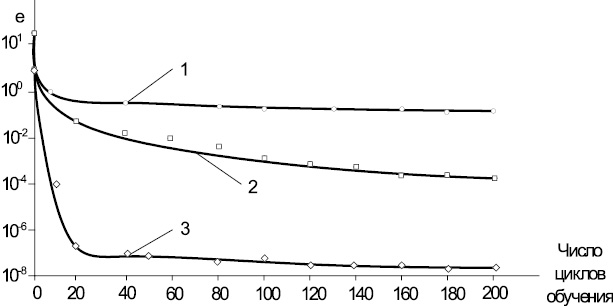
Рис. 2. Зависимость ошибки обучения НС от числа циклов обучения при различных методах: 1 – градиентного спуска; 2 – Флетчера‒Ривса; 3 – Левенберга‒Марквардта

Таблица 1

Исходная матрица планирования проведенного АПЭ с одной управляемой (х1) и двумя неуправляемыми (х1, х2) факторами

Пользуясь методом, описанным выше, найдем линейную модель. Преобразованная матрица, элементы которой находились по формуле

,

примет вид, представленный в табл. 2.

Таблица 2

Преобразованная матрица планирования

Выбрав ортогональную матрицу и сведя к ней предыдущую, сделав к неуправляемым переменным те или иные добавки, получим ортогональную матрицу, представленную в табл. 3.

Таблица 3

Ортогональная матрица планирования

По формуле (4) находим:

b2 = 1/8(– 7,2 – 0,714b2 + 0,2b3 – 8,8 + 0,429b2 + 2,6b3 + 5,2 + 0,429b2 – 0,2b3 ++ 22,8 – 0,714b2 – 3,4b3 – 10,2 + 0,143b2 + 0,6b3 –11,8 – 0,143b2 – 0,2b3 + 15,6 ++ 0,429b2 + b3 + 6,4 – 0,429b2 + b3); b2 = 1/8(12 – 0,57b2 + 1,6b3);

b3 = 1/8(–7,2 – 0,714b2 + 0,2b3 – 8,8 + 0,429b2 + 2,6b3 –5,2 – 0,429b2 + + 0,2b3 – 22,8 + 0,714b2 + 3,4b3 + 10,2 – 0,143b2 – 0,6b3 + 11,8 + 0,143b2 + 0,2b3 ++ 15,6 + 0,429b2 + b3 + 6,4 – 0,429b2 + b3); b3 = 1/8∙(8b3).

Получился случай неопределенной системы. Для устранения неопределенности заменим столбец, соответствующий переменной Z3, на другой, который придает матрице планирования свойство ортогональности. В результате получим матрицу, приведенную в табл. 4.

Таблица 4

Ортогональная матрица после устранения неопределенности

По формуле (4) находим:

b3 = 1/8(–7,2 – 0,714b2 + 0,2b3 – 8,8 – 0,429b2 – 0,6b3 + 5,2 + 0,429b2 ++ 1,8b3 – 22,8 + 0,714b2 + 3,4b3 + 10,2 – 0,143b2 + 1,6b3 –11,8 – 0,143b2 ++ b3 – 15,6 – 0,429b2 + b3 + 6,4 – 0,429b2 + b3); b3 = 1/8(– 26,8 – 1,144 b2 + 10,2b3);

b2 = 1/8(–7,2 – 0,714b2 + 0,2b3 – 8,8 + 0,429b2 + 0,6b3 + 5,2 + 0,429b2 + 1,8b3 ++ 22,8 – 0,714b2 – 3,4b3 – 10,2 + 0,143b2 – 1,6b3 –11,8 – 0,143b2 + 1,8b3 + 15,6 ++ 0,429b2 – b3 + 6,4 – 0,429b2 + b3); b2 = 1,4 – 0,07b3; b3 = 12,456; b2 = 0,528.

b1 = 1/8(–7,2 – 0,714b2 + 0,2b3 + 8,8 – 0,429b2 – 0,6b3 – 5,2 – 0,429b2 – 1,8b3 ++ 22,8 – 0,714b2 – 3,4b3 – 10,2 + 0,143b2 – 1,6b3 + 11,8 + 0,143b2 – 1,8b3 – – 15,6 – 0,429b2 + b3 + 6,4 – 0,429b2 + b3); b1 = 1/8(11,6 – 2,858b2 – 7b3);

b1 = – 9,638; b0 = 11.

Используя вычисленные коэффициенты b0, b1, b2 и b3, получим следующее уравнение:

Z = 11 – 9,638Z1 + 0,528Z2 + 12,456Z3.

Выполнив обратное преобразование, получим искомое уравнение регрессии:

у = 11 – 9,638(x1 –7,5)/3,5 + 0,528(x2 – 3)/0,875 + 12,456(x3 – 3)/1,25;

y = – 0,0531 – 2,7537x1 + 0,6035x2 + 9,9651x3. (7)

Используемые в эксперименте факторы не исчерпывают всего набора факторов НС, влияющих на Y, и кроме функционально обусловленных воздействий, связанных с тремя факторами, на Y оказывают влияние и другие факторы процесса обучения НС, например, количества циклов обучения, величина интервала прогноза. В работе также рассмотрено влияние указанных факторов и количества нейронов в скрытом слое на величину перерегулирования (σ) и степень демпфирования (ξ). Полученные уравнения регрессии имеют вид:

σ = –5,045 – 2,8557x1 + 1,14x2 – 0,0603x3;

ξ = –0,4837 + 0,0725x1 –– 0,0177x2 + 0,0171x3.

Отсутствие параллельных определений в проведенном эксперименте не позволяет дать строгую оценку адекватности полученного уравнения. Тем не менее расчетные значения перерегулирования во всех опытах, кроме одного, составляют менее 20 %, а степень демпфирования не ниже 0,84 (при значениях параметров НСМ, близких к оптимальным), что для многих промышленных систем регулирования является приемлемым. Поскольку расчетные значения перерегулирования и степени демпфирования находятся в области допустимых значений желаемого переходного процесса, можно считать, что полученные уравнения удовлетворительные и их можно рассматривать как начальные линейные приближениия к более точным зависимостям. Результаты моделирования влияния параметров НС на качество регулирования процесса биосинтеза подтверждают эффективность предложенного подхода к получению уравнений регрессии.

Рецензенты:

Червяков Н.И., д.т.н., профессор кафедры высшей алгебры и геометрии ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Ставрополь;

Лубенцов В.Ф., д.т.н., профессор кафедры «Информационные системы, электропривод и автоматика», Невинномысский технологический институт ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Невинномысск.

Работа поступила в редакцию 05.12.2012.