Исследование америция, который является ярким представителем ряда актинидов, представляет значительный научный интерес. Америций демонстрирует необычную температурную зависимость магнитной восприимчивости, при этом до сих пор отсутствуют работы, в которых бы давалось последовательное объяснение причин возникновения такой зависимости и её связи с особенностями электронной структуры америция.
В настоящей работе в рамках самосогласованной процедуры, объединяющей первопринципный расчет электронной структуры по схеме LDA + U + SO (в методе FP-LAPW) и модельные представления о тепловых спиновых и зарядовых флуктуациях в системе d-, f-электронов [1,4], рассчитывается электронная структура и температурная зависимость магнитной восприимчивости америция. При этом рассматривается обобщенная s(p)df-модель, в которой наряду с зонным движением s-, p-, d-, f-электронов и орбитальным расщеплением f-состояний учитывается внутриузельные хаббардовские ff-, dd-взаимодействия и межузельное df-обменное взаимодействие.
Для вычисления свободной энергии используется подход, который применительно к спин-флуктуационной s(p)df-модели Хаббарда развивался в работах [1, 4]. В рамках этого подхода гамильтониан взаимодействия включает слагаемые, отвечающие за внутриатомные ff- и dd-отталкивания, записываемые в рамках модели Хаббарда, а также слагаемое, ответственное за df-обменное взаимодействие. С помощью преобразования Стратоновича-Хаббарда задача о взаимодействующих электронах сводится к задаче о невзаимодействующих электронах, находящихся во флуктуирующих зарядовых и обменных полях. Далее выполняется расчет квантово-статистических средних, фигурирующих в получаемом для статистической суммы выражении с использованием теоремы Вика и суммирования получаемых при этом рядов в приближении однородных локальных полей. При этом полученные выражения учитывают эффекты магнитного (спинового) ангармонизма в произвольных порядках по величине взаимодействия спин-флуктуационных мод. Вычисленная таким образом статистическая сумма позволяет получить выражения для магнитной восприимчивости и плотности электронных состояний при конечных температурах. Наряду со спиновыми магнитными моментами учитываются орбитальные магнитные моменты электронов, поэтому в выражении для магнитной восприимчивости наряду со спиновой восприимчивостью появляется слагаемое Ван-флековского типа:
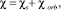 (1)
(1)
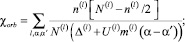 (2)
(2)
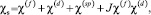 (3)
(3)
где N(l) – величина орбитального вырождения состояний l-й зоны (l = f, d); Δ(l) – среднее энергетическое расстояние между энергиями мультиплетов l-й зоны (которые расщепляются за счет кулоновского и спин-орбитального взаимодействия); U(l) – параметр хаббардовского отталкивания электронов в l-й зоны; I – однородная часть межузельного f-d-обменного взаимодействия,
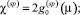 (4)
(4)
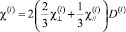 (5)
(5)
– парамагнитные восприимчивости s-, p- (4) и d-, f-электронов (5),
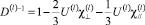 (6)
(6)
– фактор обменного усиления восприимчивости d- или f-электронов,
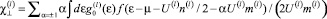 (7)
(7)
– соответствует поперечной, а
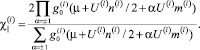 (8)
(8)
– продольной компонентам парамагнитной восприимчивости невзаимодействующих f- или d-электронов (l = f, d), среднеквадратическая амплитуда спиновых флуктуаций (квадратный корень спин-спинового коррелятора на узле)
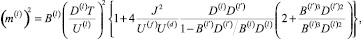 (9)
(9)
где n(l)(T) – заполнение l-й зоны, зависящее в силу спин-флуктуационного расщепления от температуры.
Важно отметить, что при расчетах плотности электронных состояний методом LDA + SO + U учитывается хаббардовский сдвиг энергий U(l)n(l)(0). Поэтому при расчете плотности состояний и энергетического спектра f- и d-электронов при T ¹ 0 учитывается только дополнительная поправка U(l)Δn(l), обусловленная возможностью температурного изменения заполнения d- и f-зон (а не U(l)n(l)(0)), что позволяет избавиться от двойного учета кулоновского взаимодействия. Параметры B(l) и X(l) являются коэффициентами разложения паулиевской восприимчивости электронов в приближении эффективной массы, 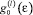 – одноэлектронная плотность состояний электронов l-й зоны (l = s(p), d, f), рассчитываемая в приближении LDA + U + SO (в базисе FP-LAPW). Самосогласование первопринципного и модельного расчетов достигается за счет того, что магнитная восприимчивость вычисляется с использованием плотности электронных состояний, полученных при том же значении U, что и в расчете магнитной восприимчивости.
– одноэлектронная плотность состояний электронов l-й зоны (l = s(p), d, f), рассчитываемая в приближении LDA + U + SO (в базисе FP-LAPW). Самосогласование первопринципного и модельного расчетов достигается за счет того, что магнитная восприимчивость вычисляется с использованием плотности электронных состояний, полученных при том же значении U, что и в расчете магнитной восприимчивости.
Расчеты электронной структуры были выполнены в пакете Elk [3]. Использовались экспериментальные данные [9] о кристаллической структуре америция, согласно которым в основном состоянии америций обладает двойной ГПУ-структурой с группой симметрии P63/mmc и четырьмя атомами в элементарной ячейке. Самосогласованно найденное значение параметра U получилось равным 2,85 эВ для f-электронов и 1,80 эВ ‒ для d-электронов, а значение JH = 0,51 эВ было определено в рамках метода, предложенного в [7], который базируется на использовании потенциала Юкавы и эффективной длины экранирования.
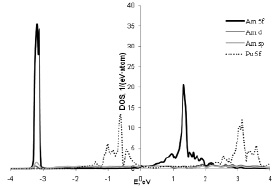
Рис. 1. Парциальные плотности электронных состояний америция; для сравнения показана также плотность состояний 5f-электронов плутония [4]
Полученные парциальные плотности электронных состояний америция показаны на рис. 1, откуда видны достаточно узкие пики, соответствующие 5f-электронам америция. Тем не менее, как видно из рис. 2, вблизи уровня Ферми плотность f-состояний становится сопоставима и на самом уровне Ферми даже меньше, чем плотности состояний s-, p- и d-электронов. В этом отношении америций существенно отличается от идущего перед ним плутония (в его наиболее важной δ-фазе), в случае которого плотность состояний f-электронов на уровне Ферми значительно выше плотности состояний d-электронов [4].
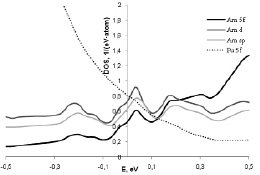
Рис. 2. Парциальные плотности электронных состояний америция вблизи уровня Ферми;
для сравнения показана также плотность состояний 5f-электронов плутония [4]
На рис. 1 и 2 в целях сопоставления показана также плотность состояний 5f-электронов δ-плутония [1], откуда видно, что в случае америция 5f5/2-подзона находится значительно дальше от уровня Ферми, чем в случае плутония, несмотря на не слишком большое отличие в параметрах хаббардовского отталкивания (U(f) = 2,85 эВ в случае америция и U(f) = 2,67 в случае δ-плутония). Этот факт может быть объяснен тем, что при переходе от плутония к америцию происходит достаточно сильная локализация 5f-электронов [6].
Результаты самосогласованных расчетов температурной зависимости магнитной восприимчивости в сопоставлении с экспериментальными данными [5, 8] показаны на рис. 3 и 4. Из рис. 3 и 4 видно, что развитая модель позволяет корректно описывать данные из обоих имеющихся источников. При этом для образца, измеренного в [5], значение константы межузельного df-взаимодействия существенно выше, чем в случае образца, измеренного в [8]. Это можно объяснить тем, что эксперимент в [5] и [8] проводился на образцах различной степени чистоты и различного «возраста», что может оказывать влияние на величину межузельного df-взаимодействия. Орбитальная восприимчивость америция составила порядка 6,5·10–4 emu·mol–1, т.е. ~54 % при 0 К и ~83 % при 300 К от величины полной восприимчивости образца, измеренного в [7] и ~68 % при 0 К и ~81 % при 300 К от величины полной восприимчивости образца, измеренного в [8].
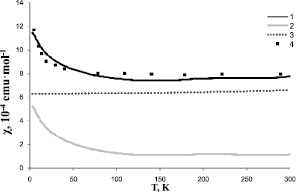
Рис. 3. Температурная зависимость магнитной восприимчивости америция:
1, 2, 3 – результат расчета в настоящей работе:
1 – полная величина восприимчивости; 2 – спиновая составляющая;
3 – орбитальная составляющая; 4 – экспериментальные данные [5]
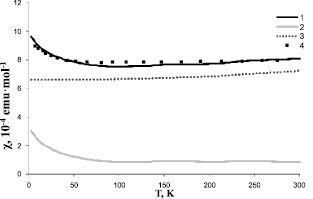
Рис. 4. Температурная зависимость магнитной восприимчивости америция:
1, 2, 3 – результат расчета в настоящей работе: 1 – полная величина восприимчивости,
2 – спиновая составляющая, 3 – орбитальная составляющая; 4 – экспериментальные данные [8]
Величина спиновой восприимчивости больше в случае образца, измеренного в [5], однако в обоих случаях спиновая восприимчивость состоит из примерно одинаковых вкладов f- и d-электронов, а также составляющей, связанной с df-обменом и незначительного вклада s(p)-электронов. Таким образом, f- и d-электроны америция играют примерно одинаковую роль в формировании спиновой составляющей его магнитной восприимчивости, что обусловлено сопоставимыми плотностями f- и d-состояний америция на уровне Ферми, и что существенно отличает его от плутония [4]. Следует отметить, что приведенные выше значения для орбитальной восприимчивости несколько превышают значения, получаемые непосредственно на основе формулы (9) и поэтому для получения наилучшего согласия с экспериментальными данными нами был учтен дополнительный постоянный вклад, который связан с орбитальным магнитным
моментом.
Было обнаружено, что необычный ход температурной зависимости магнитной восприимчивости америция обусловлен сосуществованием в нем электронных состояний двух типов. При низких температурах доминируют состояния с преобладающей поперечной компонентой магнитной восприимчивости, что эквивалентно наличию локальных магнитных моментов [2, 4] – этим объясняется возникновение при низких температурах кюри-подобной магнитной восприимчивости. С возрастанием температуры начинают преобладать состояния, обуславливающие рост продольной восприимчивости (причем это происходит быстрее для образца, измеренного в [8]), в то время как состояния, ответственные за формирование кюри-подобной восприимчивости, ослабляются. Состояния, обуславливающие рост продольной восприимчивости подобны итинерантным электронным состояниям, магнитная восприимчивость которых практически не зависит от температуры, т.е. является паулиевской. В этом отношении америций демонстрирует поведение, обратное плутонию и ряду других почти магнитных металлов [2, 4], для которых наблюдается обратный переход – от паулиевской к кюри-подобной температурной зависимости магнитной восприимчивости.
Важно подчеркнуть, что согласно полученным нами данным, участок на температурной зависимости магнитной восприимчивости америция, где она практически является постоянной, не является «хвостом» кюри-вейссовской восприимчивости, обусловленной, например, присутствием магнитной примеси, как предполагалось ранее [5], а является результатом увеличения числа итинерантных электронных состояний, которое приводит к подавлению формирования температурно-индуцированных локальных магнитных моментов. Поэтому полученные результаты необходимо учитывать для корректных оценок концентрации примесей и дефектов (в том числе радиационных) в америции и системах на его основе.
Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы (Соглашение № 14.A18.21.0737).
Рецензенты:Ивлиев А.Д., д.ф.-м.н., профессор кафедры физики ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», г. Екатеринбург;
Сидоренко Ф.А., д.ф.-м.н., профессор кафедры физики ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 26.10.2012.



