Природа магнитных и электронных свойств актинидов является одной из нерешенных проблем физики сильно коррелированных электронных систем [4]. Важную группу этих веществ образуют почти магнитные металлы, сплавы и соединения (например, на основе плутония и америция). Особенностью почти магнитных металлических систем на основе 5f-металлов является проявляющаяся при изменении электронной концентрации неустойчивость не только к формированию магнитного упорядочения, но и сверхпроводимости. Яркие проявления этих неустойчивостей демонстрируют, наряду с самими 5f-металлами, сплавы и соединения на их основе [7, 3].
Цель работы – исследование спин-флуктуационного механизма спаривания сильно коррелированных электронов в рамках двузонной модели Хаббарда, в которой наряду с зонным движением f- и d-электронов учитываются внутриатомные кулоновские и межузельные обменные взаимодействия и анализ полученных выражений на примере PuRhGa5.
Материал и методы исследований
Сверхпроводимость соединения PuRhGa5 возникает при температуре 8,9 K [3], а его нормальная фаза характеризуется парамагнитной восприимчивостью, описываемой законом Кюри‒Вейсса. Механизм образования куперовских пар в этом соединении не установлен. При этом, согласно [6], фононный механизм синглетного спаривания электронов (теория БКШ) в изоструктурном PuCoGa5 не дает согласия с экспериментальными данными о температуре ТС .
Существующие подходы к описанию электронной структуры в рамках первопринципных расчетов дают оценочные значения параметров внутриатомного взаимодействия f-электронов, соответствующих режиму сильных хаббардовских корреляций (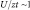 ,
,
U – параметр внутриатомного хаббардовского взаимодействия, t – интеграл перескока, z – число ближайших соседей), что соответствует области кроссовера локализованной и коллективизированной моделей [4, 8]. Кроме того, электронная подсистема рассматриваемого соединения включает в себя две группы взаимодействующих между собой сильно коррелированных f- и d-электронов и не описывается в рамках первопринципных подходов, основанных на использовании однозонной модели Хаббарда. Поэтому целесообразно провести ее исследование в рамках обобщенной многозонной модели Хаббарда, в которой наряду с зонным движением d- и f-электронов учитывается их внутриатомное кулоновское и обменное взаимодействия:
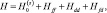 (1)
(1)
где 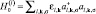 – гамильтониан невзаимодействующих s(p)-, d- или f-электронов (l = s(p), d, f); εl,k– одноэлектронные зонные энергии;
– гамильтониан невзаимодействующих s(p)-, d- или f-электронов (l = s(p), d, f); εl,k– одноэлектронные зонные энергии; 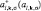 –
–
оператор рождения (уничтожения) электронов (l = s(p), d, f) с квазиимпульсом k и спиновым квантовым числом s = ±1; 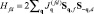 – гамильтониан межузельного обменного взаимодействия f- и d-электронов;
– гамильтониан межузельного обменного взаимодействия f- и d-электронов; 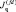 – Фурье-образ параметра межузельного fd-обменного взаимодействия
– Фурье-образ параметра межузельного fd-обменного взаимодействия 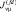 ; Hff и Hdd – гамильтонианы систем f- и d-электронов, имеющие одинаковую структуру, включающие в себя гамильтонианы невзаимодействующих электронов –
; Hff и Hdd – гамильтонианы систем f- и d-электронов, имеющие одинаковую структуру, включающие в себя гамильтонианы невзаимодействующих электронов –
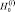 (l = f или d) и гамильтониан внутриатомного хаббардовского отталкивания на узле, который может быть записан через Фурье-образы операторов зарядовой и спиновой плотности (см., например, [5]):
(l = f или d) и гамильтониан внутриатомного хаббардовского отталкивания на узле, который может быть записан через Фурье-образы операторов зарядовой и спиновой плотности (см., например, [5]):
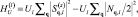 (2)
(2)
где Ul – параметр внутриатомного кулоновского отталкивания электронов (l = d, f); 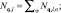
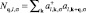 – Фурье-образ оператора плотности числа электронов на узле со спином s; q –
– Фурье-образ оператора плотности числа электронов на узле со спином s; q –
квазиимпульс; Sq,l – Фурье-образ оператора вектора спиновой плотности электронов; 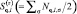 –
–
его z-проекция.
Для анализа условий возникновения сверхпроводящей фазы за счет синглетного спаривания l-электронов рассмотрим нормальную и аномальную функции Грина:
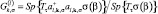
и
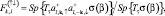 (3)
(3)
где 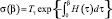 – матрица рассеяния, определяющая статистическую сумму
– матрица рассеяния, определяющая статистическую сумму 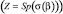 , рассматриваемой сильно коррелированной электронной системы; H(τ) – гамильтониан (1) в мацубаровском представлении взаимодействия; Tτ – оператор упорядочения по мацубаровскому времени τ.
, рассматриваемой сильно коррелированной электронной системы; H(τ) – гамильтониан (1) в мацубаровском представлении взаимодействия; Tτ – оператор упорядочения по мацубаровскому времени τ.
Вычисления функций (3) были выполнены в рамках интерполяционной спин-флуктуационной теории, основанной на использовании преобразования Стратоновича‒Хаббарда, сводящего рассматриваемую квантово-статистическую задачу многих тел к изучению движения свободных электронов во флуктуирующих в пространстве и во времени внутренних стохастических обменных (ξl,ν) и зарядовых (ηl,ν) полях [1, 2]. В первом приближении по аномальному среднему и в приближении однородных локальных полей [1] система уравнений Элиашберга может быть сведена к одному уравнению:
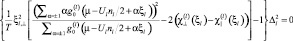 (4)
(4)
где 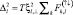 отвечает сверхпроводящей щели и выражается через аномальное среднее.
отвечает сверхпроводящей щели и выражается через аномальное среднее.
Результаты исследования и их обсуждение
Переходя к численному анализу парамагнонного спаривания в PuRhGa5, воспользуемся для расчета одноэлектронной плотности состояний методом LDA + U + SO
(в базисе FP-LAPW). Однако, поскольку основное состояние данного соединения является сверхпроводящим, расчеты энергетических спектров могут быть выполнены лишь в области температур, соответствующих нормальной фазе (T > ТC). Поэтому целесообразно использовать ранее развитый нами метод самосогласованного расчета плотности электронных состояний [2], объединяющий первопринципный расчет электронной структуры с модельным численным расчетом амплитуды FSD и магнитной восприимчивости. Выражение для восприимчивости получается путем добавления к (1) слагаемого, описывающего зеемановский сдвиг, и последующего дифференцирования по магнитному полю статистической суммы 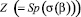 , вычисленной методом перевала (см., например, [5]):
, вычисленной методом перевала (см., например, [5]):
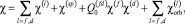 (5)
(5)
где
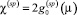 и
и 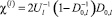
– парамагнитные восприимчивости s(p)- и d,f-электронов; 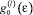 – одноэлектронная плотность состояний электронов l-й зоны;
– одноэлектронная плотность состояний электронов l-й зоны;
µ – химический потенциал;
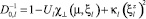
– фактор обменного усиления парамагнитной восприимчивости d- или f-электронов; ξl – среднеквадратическая амплитуда флуктуаций стохастических полей;
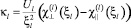
– коэффициенты спиновой жесткости в системе l-электронов; 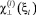 и
и 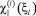 – поперечная и продольная компоненты паулиевской восприимчивости f-, d-электронов с учетом спин-флуктуационной перенормировки их спектров:
– поперечная и продольная компоненты паулиевской восприимчивости f-, d-электронов с учетом спин-флуктуационной перенормировки их спектров:
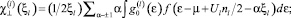
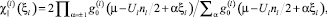
где 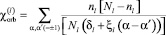 – орбитальная восприимчивость d- или f-электронов [2]; Nl – величина орбитального вырождения состояний l-й зоны (l = f, d); nl – занятые состояния; δl – среднее энергетическое расстояние между энергиями мультиплетов l-й зоны;
– орбитальная восприимчивость d- или f-электронов [2]; Nl – величина орбитального вырождения состояний l-й зоны (l = f, d); nl – занятые состояния; δl – среднее энергетическое расстояние между энергиями мультиплетов l-й зоны; 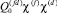 – вклад f-d-обмена в магнитную восприимчивость.
– вклад f-d-обмена в магнитную восприимчивость.
В свою очередь, в приближении эффективной массы температурная зависимость модуля обменного стохастического поля на узле описывается уравнением [1]:
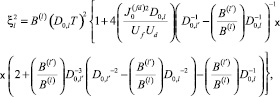
где B(l) – коэффициент разложения паулиевской восприимчивости по частоте,
а 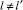 .
.
Результаты расчетов плотности электронных состояний и магнитной восприимчивости представлены на рис. 1, 2.
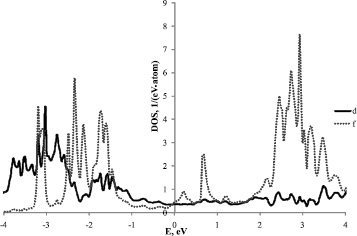
Рис. 1. Плотность состояний d- и f-электронов PuRhGa5
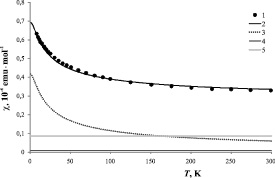
1 – экспериментальные данные [3]; 2 – полная магнитная восприимчивость, рассчитанная
по формуле (3); 3 и 4 – вклады f- и d-электронов соответственно; 5 – орбитальный вклад
Сопоставление результатов расчетов с экспериментальными данными [3] проведено для значений параметров внутриатомного межэлектронного взаимодействия: Uf = 2,1 эВ, Ud = 1,5 эВ хундовского обменного взаимодействия JH = 0,85 эВ и межузельного fd-обменного взаимодействия J(fd) = 0,25Uf эВ. Среднее расстояние между мультиплетными энергиями δl = 2,5 эВ, что соответствует половине энергетического расстояния между центрами зон, отвечающих f- и d-мультиплетам. Кроме этого, при расчете восприимчивости использовались параметры мнимой части функции Линхарда f- и d-электронов: B(f) = 0,55 и
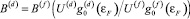 .
.
Как следует из анализа полученных зависимостей, орбитальный вклад в магнитную восприимчивость в основном обусловлен f-электронами. Оставаясь по величине практически неизменным (рис. 2), он возрастает по относительной величине от 10–2 до 20 %.
Обращает на себя внимание паули-подобное изменение магнитной восприимчивости d-электронов (см. рис. 2). Такое поведение c(d)(Т) обусловлено слабой зависимостью плотности состояний d-электронов от энергии вблизи положения химического потенциала (см. рис. 1). Последнее ведет к тому, что имеющие место перенормировки спектра этой группы электронов оказываются не существенными, а константа спиновой жесткости мала и положительна. Относительный вклад d-электронов в c(Т) возрастает с температурой от ≈10 до 45 %.
Основной вклад в зависимость c(Т) вносят f-электроны, относительная величина которого изменяется от 90 до 40 % при изменении температуры от 0 К до 300 К. Восприимчивость этой группы электронов описывается обобщенным законом Кюри‒Вейсса (см. рис. 2). Из-за наличия в непосредственной близости от положения химического потенциала локального максимума на зависимости 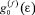 спин-флуктуационные перенормировки спектра f-электронов оказываются значительными, вследствие чего флуктуации спиновой плотности близки к насыщению (см., например, [1, 2]). Однако вследствие перераспределения электронов между f-, d- и sp-состояниями и обусловленного межзонным обменным взаимодействием взаимного «подмагничивания» f- и d-подсистем эффект насыщения амплитуды FSD в системе f-электронов не достигается. Поэтому константа спиновой жесткости отрицательна и резко изменяется с температурой.
спин-флуктуационные перенормировки спектра f-электронов оказываются значительными, вследствие чего флуктуации спиновой плотности близки к насыщению (см., например, [1, 2]). Однако вследствие перераспределения электронов между f-, d- и sp-состояниями и обусловленного межзонным обменным взаимодействием взаимного «подмагничивания» f- и d-подсистем эффект насыщения амплитуды FSD в системе f-электронов не достигается. Поэтому константа спиновой жесткости отрицательна и резко изменяется с температурой.
Анализ уравнения (6) с использованием найденных значений Ul, εF и плотность электронных состояний показывает неустойчивость к формированию сверхпроводимости в системе f-электронов. При этом в силу положительности константы спиновой жесткости для d-электронов спин-флуктуационный механизм сверхпроводимости в этой подсистеме не реализуется. Оценка температуры сверхпроводящего перехода, выполненная на основе установленной электронной структуры PuRhGa5, дает величину TС = 10 К (экспериментальное значение 8,9 K [3]) при 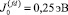 .
.
При этом следует отметить, что уменьшение значения 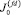 ведет к резкому падению величины TС.
ведет к резкому падению величины TС.
Заключение
Таким образом, спиновые флуктуации могут являться причиной возникновения сверхпроводимости PuRhGa5. Усилению неустойчивости к возникновению сверхпроводимости способствует межзонное взаимодействие. При этом из полученных формул следует сильная зависимость температуры Тс от концентрации электронов, что указывает на важность экспериментальных исследований допированных систем, обеспечивающих возможность контролируемого изменения концентраций d- или f-электронов.
Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 гг. (соглашение № 14.А18.21.0737).
Рецензенты:
Коршунов И.Г., д.ф.-м.н., профессор, заведующий кафедрой, Уральский государственный горный университет, г. Екатеринбург;
Попель П.С., д.ф.-м.н., профессор, заведующий кафедрой, Уральский государственный педагогический университет,
г. Екатеринбург.
Работа поступила в редакцию 26.10.2012.



