Знание закономерностей дефектообразования в полупроводниковых материалах типа кремния и германия имеет исключительное значение, так как они являются основными материалами современной полупроводниковой электроники, солнечной энергетики и космической техники.
Процессы дефектообразования в кремнии и германии хорошо известны. Большое количество работ описывают причины, особенности и критерии формирования дефектов в этих материалах. Однако существенно меньше работ, описывающих зависимость образования дефектов от энергии дефекта упаковки (ЭДУ). Энергия дефекта упаков-
ки – качественная характеристика любого полупроводникового материала. Она показывает необходимые условия для образования структурных дефектов (главным образом, линейных и объёмных). Определение ЭДУ в кремнии и германии позволяет не только установить дефектостойкость данных материалов, но и определить предельную плотность дефектов и произвести расчет ряда дополнительных параметров, например, критического радиуса дислокационных петель,что позволит более эффективно использовать данные материалы в современных наносистемах.
Целью исследования явилось установление закономерности между энергией дефекта упаковки и критическими радиусами дислокационных петель в кремнии и германии.
Материал и методы исследования
Исследуются монокристаллы кремния и германия, выращенные в Красноярском крае. Для выполнения цели исследования образцы изучались методами просвечивающей электронной микроскопии (ПЭМ), главной целью которых являлось обнаружение и анализ структурных дефектов в данных материалах, а также проведение дополнительных испытаний, необходимых для дальнейшего вычисления ЭДУ материалов. При помощи просвечивающего электронного микроскопа JEOL JEM 2100 идентифицировались структурные дефекты в образцах кремния и германия, в дальнейшем была установлена их плотность. Были вычислены параметры дефектов и их характеристики. Предварительно образцы тщательно подготавливались для электронно-микроскопических исследований с применением современных методов пробоподготовки. Последний этап включал в себя ионное травление аргоном при оптимальных условиях для кремния и германия (рис. 1), что исключило возможность возникновения в материалах дополнительных дефектов, а также внесение примеси. Непосредственное исследование в ПЭМ JEOL JEM 2100, оснащенного рядом устройств, позволило определить именно структурные дефекты, отделив от них экстинкционные контуры и прочие артефакты [4].
а) б)
б)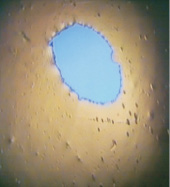
Рис. 1. Ионное травление образцов:
а – установка Precision Ion Polishing System (PIPS), Gatan; б – образец после ионного травления
Полученные результаты позволили вычислить ЭДУ в материалах по методу определения ширины полосок дефекта упаковки. А в дальнейшем вычислить критический радиус дислокационных петель с применением классической модели частичных дислокационных петель в двух случаях: классическом (с учетом энергий дефекта упаковки дислокационной петли и упругой энергии дислокационной линии) и с учетом формирования частичных дислокаций Шокли.
Результаты исследования и их обсуждение
Исследования на просвечивающем электронном микроскопе показали, что образцы кремния и германия содержат незначительное количество структурных дефектов: дислокаций, дислокационных петель и дефектов упаковки (рис. 2, 3). Плотность дефектов составила 104–105 см2 для кремния и 104 см2 ‒ для германия.
ЭДУ вычислялась по методу определения ширины полоски дефекта упаковки [1, 3], т.е. по расстоянию, на которое разбегаются частичные дислокации. Ширина полоски вычисляется по формуле:
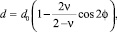 (1)
(1)
где 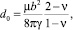 (2)
(2)
отсюда
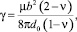 (3)
(3)
где ν – коэффициент Пуассона; φ – угол между полным вектором Бюргерса и направлением полоски; b – вектор Бюргерса; γ – ЭДУ; μ – модуль сдвига.
Вычисленное значение энергии дефекта упаковки составило 5∙10–2 и 9∙10–2 Дж/м2 для кремния и германия соответственно. Полученные данные по ЭДУ свидетельствуют о том, что монокристаллический германий имеет более высокую энергию дефекта упаковки, чем монокристаллический кремний, а значит, он более стоек к образованию дефектов. Это подтверждается экспериментально: плотность дефектов в германии существенно меньше, чем в кремнии.
Известно, что плотность и размеры дислокационных петель напрямую связаны с энергией дефекта упаковки [2–3], так как один из вариантов образования дислокационных петель происходит при наличии частичных дислокаций, замыкающихся сами на себя. Как показали исследования на просвечивающем электронном микроскопе, эти дислокации были дислокациями Франка. Особое внимание было обращено на радиусы дислокаций Франка, так как предполагается, что они связаны со значением ЭДУ в материале. Вычислив значение ЭДУ, теперь возможно рассчитать критический радиус дислокационных петель в кремнии и германии. Стоит отметить, что критический радиус дислокационной петли ‒ та важная характеристика, которая показывает те точки, после которых происходят качественные и количественные изменения дефектной сети материала.
а)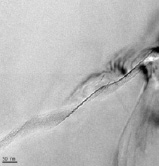 б)
б)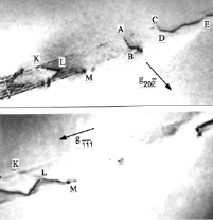
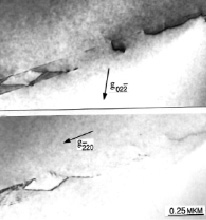
Рис. 2. Структурные дефекты в кремнии:
а – дислокация; б – дефект упаковки: AB, CD – винтовые дислокации (вектор Бюргерса b параллелен линии дислокации l; см рис. 4 а и г. На г исчезает дислокация при (gb) = 0, где g – вектор дифракции), DE – краевая, KL – смешанная дислокация
Для вычисления критического радиуса дислокационной петли (rcrit) нами используется классическая модель описания энергий процесса образования петель Франка. Согласно ей общая энергия образования дислокационной петли (El,perfect) включает в себя энергию дефекта упаковки дислокационной петли (ESF) и упругую энергию дислокационной линии (El,Frank) (1) [6]. Однако энергия El,perfect еще может быть выражена как сумма энергий двух петель с вектором Бюргерса b = bin + bout.
El,perfect = ESF + El,Frank, (4)
где ESF = πr2γ; (5)
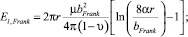 (6)
(6)
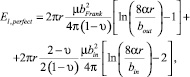 (7)
(7)
где r – радиус дислокационной петли; µ – модуль сдвига; υ – коэффициент Пуассона; α – фактор ядра дислокации; bFrank – модуль вектора Бюргерса дислокационной петли Франка. В случае образцов кремния и германия (рис. 2–3) получается:
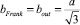 и
и 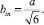
Таким образом, из (4–7) получаем связь между критическим радиусом (rcrit) и энергией дефекта упаковки (γ) как:
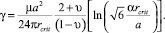 (8)
(8)
а)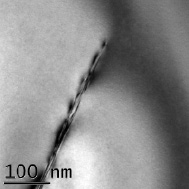 б)
б)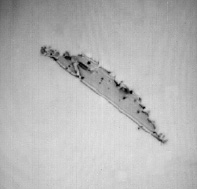
Рис. 3. Структурные дефекты в германии:
а – дислокация; б – дефект упаковки
Решив трансцендентное уравнение, получим значения rcrit (таблица).
Численные значения ЭДУ и rcrit кремния и германия
|
Материал |
ЭДУ, мДж/м2 |
rcrit (классическая модель), нм |
rcrit (с учетом частичных дислокаций Шокли), м |
|
Si |
55 |
98,8 |
18,0 |
|
Ge |
90 |
55 |
9,9 |
Однако классическая модель описания энергий процесса образования частичных дислокационных петель имеет ряд недостатков, в частности, в ней не учитывается, что при этом процессе образование вакансионной петли Франка происходит путем формирования частичных дислокаций Шокли, что является наиболее энергетически выгодным. В этом случае формула (4) приобретает вид:
El,perfect = ESF + El,Frank + 2EShockley, (9)
где 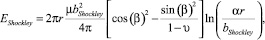 (10)
(10)
где β – угол между вектором Бюргерса и дислокационной линией сегмента Шокли, в нашем случае – β = π/6, 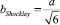 .
.
Стоит обратить внимание, что частичные дислокации Шокли считаются как прямые отрезки, а не как петли, хотя общая линия двух дислокаций образует петлю. Для проверки данной модели был вычислен критический радиус, и полученные результаты сравнивались с данными, полученными с помощью классической модели.
Из уравнения (9) можно получить выражение для γ процесса образования внешней петли:
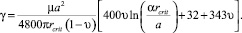 (11)
(11)
Численные результаты приводятся
в таблице.
Заключение
В работе были проведены электронно-микроскопические исследования монокристаллов кремния и германия. Было определено значение энергии дефекта упаковки: 5∙10–2 и 9∙10–2 Дж/м2 для кремния и германия соответственно. Подтверждена зависимость плотности дефектов от ЭДУ: в кремнии, где ЭДУ несколько ниже, чем в германии, наблюдалось существенно более высокая плотность дефектов. Также, используя модель описания энергий процесса образования частичных дислокационных петель, были вычислены критические радиусы дислокационных петель данных материалов. В классическом случае (учитывая только энергию петель Франка) и с учетом энергии, вносимой частичными дислокациями Шокли. Установлено, что во втором случае полученные критические радиусы дислокационных петель достаточно точны, что подтверждается сравнением результатов с данными ряда работ [3, 5]. А также подтверждено предположение о влияние ЭДУ на rcrit, согласно данным таблицы.
Экспериментальная работа была проведена при поддержке гранта ФЦП РФ НК-550P_2.
Рецензенты:
Логинов Ю.Ю., д.ф.-м.н., профессор, Сибирский государственный аэрокосмический университет им. ак. М.Ф. Решетнева, г. Красноярск;
Попов А.М., д.ф.-м.н., профессор, Сибирский государственный аэрокосмический университет им. ак. М.Ф. Решетнева, г. Красноярск.
Работа поступила в редакцию 26.10.2012.



