Известны [1] сеточные базисы ортогональных финитных функций (ОФФ) (первый такой базис построен В.Л. Леонтьевым в 1993 году [2], другие подобные базисы созданы и исследованы затем, например, в [3, 4, 5]), состоящие из финитных непрерывных функций, и такие, что скалярные произведения функционального пространства L2 любых двух различных функций каждого такого базиса на каждой конкретной сетке равны нулю. Ранее (в 1988 году) были построены финитные ортогональные вейвлеты И. Добеши [6], но они в отличие от базисных функций [1] не могут быть записаны в аналитической форме, строятся приближенно с заданной точностью с помощью итерационного алгоритма кратноразрешающего анализа, не обладают симметрией (четностью, нечетностью), имеют существенно более сложную структуру и низкую гладкость. Базисные функции [6] построены с целью их использования в спектральном анализе сигналов, где успешно применяются, но не адаптированы к их использованию в алгоритмах численно-аналитических методов (проекционно-сеточных (ПСМ) и вариационно-сеточных (ВСМ)). Функции [1] созданы специально для их применения в алгоритмах численно-аналитических методов, связанных со смешанными вариационными принципами (Рейсснера, Ху-Васидзу) или с обобщающими эти вариационные принципы смешанными проекционными условиями. Показано [1], что использование ОФФ устраняет основной недостаток смешанных ВСМ или ПСМ – в несколько раз более высокое число узловых неизвестных по сравнению с ВСМ, основанными на вариационном принципе Лагранжа. Ортогональность таких базисных финитных функций позволяет исключить большую часть узловых неизвестных величин до начала решения глобальной сеточной системы линейных алгебраических уравнений (СЛАУ) на ЭВМ (число исключаемых величин в 2-4 раза превышает число остающихся в СЛАУ узловых величин), тем самым по числу арифметических операций, необходимых для получения решения СЛАУ, ВСМ, основанные на вариационном принципе Рейсснера, оказываются близкими к ВСМ, основанным на вариационном принципе Лагранжа. При этом качество решений для всех величин (не только для основных неизвестных функций, например, перемещений, но и для их производных, например, деформаций и напряжений) в смешанном ВСМ или ПСМ является существенно более высоким и по точности, и по гладкости, чем в ВСМ, связанном с вариационным принципом Лагранжа.
1. В последние годы в связи с развитием алгоритмов численных методов возник вопрос: возможно ли построение базисных ОФФ, обладающих дополнительными свойствами. В [1] и более ранних работах В.Л. Леонтьева отмечалось, что ряд таких ОФФ имеет неиспользованные для придания функциям свойства ортогональности свободные параметры, которые можно использовать для появления у этих функций дополнительных свойств. Однако, оказывается, что эти дополнительные свойства не могут планироваться произвольно. Здесь показывается, что невозможно создание финитных функций Лагранжева базиса (в таком базисе каждая отдельная функция базиса определяет значение глобальной аппроксимации функции или ее производной только в одном узле), которые, во-первых, обладают свойствами: взаимно-ортогональными являются сами базисные функции, а также каждая функция является ортогональной первым производным всех других функций этого базиса на каждой конкретной сетке, и, во-вторых, предназначены для полноценного использования их в проекционных условиях.
Пусть
{… < xj–2 < xj–1 < xj < xj + 1 < xj + 2 < …}
– координаты узлов сетки, расположенных на действительной оси.
Теорема. Пусть {φi(x)} – сеточный Лагранжев «базис» в L2 (R) такой, что
φi(xj) = δij,
тогда если функции φi(x) обладают следующими свойствами ортогональности
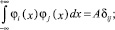
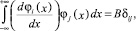(1)
где A, B – некоторые числовые константы, то они не могут быть использованы для аппроксимации неизвестных функций при построении приближенных решений в проекционных условиях, связанных с невязками дифференциальных уравнений, содержащих неизвестные функции и их первые производные.
Доказательство.
Пусть f1(x), f2(x) – непрерывные функции, первая из которых строго возрастает, а вторая строго убывает на интервале
(xj–2, xj+2), причем
f1(xj) = f2(xj). (2)
Пусть также
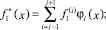
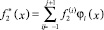
– аппроксимации функций f1(x), f2(x) на интервале (xj–1, xj+1) линейными комбинациями функций φi(x). Здесь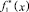 
– строго возрастающая функция; 
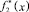– строго убывающая функция, причем
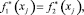
где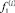 
, 
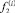– постоянные коэффициенты, равные значениям f1(x), f2(x) в узлах xi.
Скалярные произведения первых производных этих аппроксимаций и φj(x)
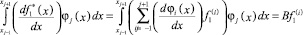
и
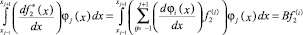
равны в силу (1) и (2). Это означает, что в проекциях первых производных двух различных функций – строго возрастающей и строго убывающей, отличных от нуля и имеющих различные знаки, ‒ информация о первых производных двух различных в окрестности точки xj функций при проецировании аппроксимаций этих первых производных теряется. Таким образом, использование подобных функций в качестве базисных в проекционных условиях методов типа Бубнова‒Галеркина применительно к невязкам дифференциальных уравнений невозможно. Следовательно, расщепление системы сеточных уравнений на совокупность несвязанных уравнений с помощью такого ПСМ невозможно.
2. Рассмотрим общий случай. Пусть
f(x) ‒ материнская локальная (финитная) функция, обладающая на отрезке [–1, 1] свойствами
f(–1) = f(1) = 0; f(0) = A,
где A не равно нулю и равно, например, единице, и обладающая также свойством
f(x) + f(x – 1) = f(0) ∀ x ∈ [0, 1], (3)
необходимым для наличия у последовательности сеточных наборов функций, порожденных этой материнской функцией, полного набора свойств системы базисных функций. За пределами отрезка [–1, 1] функция f(x) тождественно равна нулю.
Предположим, что сеточные функции, порожденные материнской функции f(x), обладают не только известным свойством ортогональности [1] самих сеточных функций на каждой конкретной сетке (внутригрупповой взаимной ортогональностью финитных базисных функций)
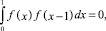(4)
но и дополнительным свойством внутригрупповой ортогональности производных сеточных функций самим сеточным функциям
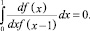(5)
Пусть на отрезке [–1, 1] материнская функция модифицируется, во-первых, некоторой финитной функцией αφ(x) (α – постоянный коэффициент), имеющей конечный носитель, не выходящий за пределы отрезка [0, 1], а, во-вторых, финитной функцией (–αφ(–x)) с конечным носителем, не выходящим за пределы отрезка [–1, 0]. Первая модифицирующая функция симметрична относительно линии x = 0,5, вторая – относительно линии x = –0,5. В этом случае функция f(x – 1) на отрезке [0, 1] имеет соответствующую модификацию, определяемую функцией (–αφ(x)) и поэтому свойство (3) выполняется для модифицированных сеточных функций автоматически в случае, если до модификации сеточные функции им обладают. Последнее здесь предполагается, поскольку рассматривается модификация базисных функций с целью изучения вопроса возможности возникновения у них дополнительного свойства, а именно, свойства ортогональности производных сеточных функций, с одной стороны, и самих сеточных функций, с другой стороны. Далее предполагается также, что модифицирующие функции непрерывны и имеют в точках x = 0,± 1 значения, равные нулю.
Условия (4), (5) с учетом такой модификации записываются в виде
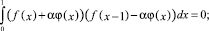
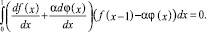
Пусть
ψ(x) = f(x) + αφ(x)
на [0, 1], тогда последние два условия c учетом (3) записываются в виде
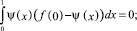
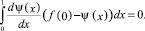
Выполнение первого из двух последних условий обеспечивается при определенном выборе числовых значений коэффициента α, которые, как показано в [1], существуют. Рассмотрим второе условие, которое переписывается в виде
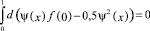
или
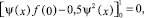
откуда получается
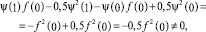
поскольку
ψ(0) = f(0) = A ≠ 0; ψ(1) = f(1) = 0,
а следовательно, второе условие не выполняется при любом выборе модифицирующей функции φ(x) и значений параметра α.
Заключение
Известные примеры численно-аналитических «методов», в рамках которых последние три года строятся и используются «базисные» системы финитных функций, «обладающих» свойствами ортогональности как функций, так и их первых производных, являются неверными в своей основе. Такое заключение основано здесь не только на представленных формальных математических исследованиях, но и на том, что в итоге применения в рамках подобного «метода» процедуры проецирования, связанной с сеткой, каждое уравнение во внутреннем узле сетки оказывается не имеющим никакой связи ни с уравнениями в других узлах, ни с граничными условиями. Возникает естественный вопрос: почему подобное расщепление системы проекционных уравнений возможно для нефинитных функций, например, как известно, для тригонометрических? Это возможно потому, что, несмотря на отделение проекционных уравнений друг от друга в смысле наборов содержащихся в них коэффициентов из состава аппроксимирующих точное решение линейных комбинаций, каждое возникающее после применения процедуры проецирования уравнение, соответствующее отдельной базисной тригонометрической функции, учитывает внешнее воздействие на моделируемую систему на всей области краевой задачи в силу нефинитности базисной функции и при этом любое из таких уравнений может учитывать в общем случае граничные условия.
Рецензенты:
Вельмисов П.А., д.ф.-м.н., профессор, заведующий кафедрой «Высшая математика» Ульяновского государственного технического университета, г. Ульяновск;
Журавлев В.М., д.ф.-м.н., профессор, профессор кафедры «Теоретическая физика» Ульяновского государственного университета, г. Ульяновск;
Попов Ф.А., д.т.н., профессор, зам. директора по ИТ, Бийский технологический институт, г. Бийск.
Работа поступила в редакцию 26.10.2012.