Как показывают экспериментальные наблюдения, метеорологические параметры существенно изменяются на протяжении суток и напрямую влияют на характер распространения загрязнений в атмосфере. В связи с этим при моделировании распространения примесей загрязняющих веществ от непрерывных источников загрязнений необходимо учитывать изменение метеорологических параметров во времени. Вертикальная диффузия турбулентных движений масс воздуха, направление и скорость ветра непрерывно и существенно изменяются на протяжении суток. Как правило, для анализа степени загрязнения используются стационарные модели распространения загрязнений [6, 7], не учитывающие изменение метеорологических параметров во времени. Как показано, учет временных флуктуаций атмосферных параметров в приповерхностном слое атмосферы позволит существенным образом уменьшить погрешность при расчете полей поверхностных загрязнений.
Проведен ряд компьютерных экспериментов по исследованию накопления загрязняющего вещества за десятидневный период подстилающей поверхностью от непрерывного высотного точечного источника загрязнения высотой 107 метров. Цель исследования заключалась в определении степени влияния динамических изменений атмосферных параметров на результирующее поле поверхностного загрязнения за время моделирования, а также определении наилучшего метода аппроксимации скорости ветра для достижения наименьшей ошибки моделирования. Моделирование осуществлялось с помощью разработанного программного комплекса имитационного моделирования, созданного на основе метода клеточных автоматов [1, 2, 3].
Комплекс программ состоит из набора модулей (программ), по отдельности обеспечивающих расчеты массопереноса в результате моделирования следующих физических процессов:
• эмиссии загрязняющих веществ;
• конвективного массопереноса вдоль направления ветра;
• седиментации (гравитационного осаждения, сухого осаждения);
• турбулентной диффузии;
• вторичного ветрового массопереноса;
• адсорбции молекул воды на поверхности аэрозольных частиц;
Основная особенность реализации указанного программного комплекса заключается в применении метода объединения правил клеточного автомата для моделирования комплексного процесса массопереноса загрязняющих веществ в атмосфере. Правила объединяются с учетом их интенсивности влияния на процесс рассеивания массопереноса
Основным показателем интенсивности правила КА является его характерное время, рассчитанное исходя из выделенных безразмерных комплексов атмосферных процессов (3, 4, 5). Результатом объединения правил являются рассчитанные вероятности срабатывания каждого правила КА.
T∙P = b (1)
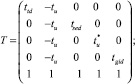
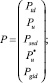
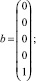 (2)
(2)
ttd = Ptd∙Dca∙L2/(D∙Lca2); (3)
tu = Pu∙L∙uca/(Lca∙u); (4)
tsed = Psed∙ωca∙L/(Lca∙ω); (5)
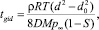 (6)
(6)
где T ‒ матрица характерных времен процессов; P ‒ искомая матрица вероятностей; b ‒ вектор свободных коэффициентов; ttd ‒ характерное время процесса диффузии; Ptd ‒ вероятность правила диффузии КА;
L и Lca ‒ размер моделируемой области пространства в метрах и размер вектора состояний клеточного автомата соответственно; Dca ‒ безразмерный коэффициент диффузии клеточного автомата; D ‒ коэффициент диффузии м2/с; tu ‒ характерное время процесса ветрового массопереноса; Pu ‒ вероятность правила ветрового массопереноса КА; uca ‒
безразмерная скорость ветрового массопереноса клеточного автомата; u ‒ средняя скорость ветра м/с; tsed ‒ характерное время процесса гравитационного осаждения; ωca ‒
безразмерная скорость гравитационного осаждения клеточного автомата; ω ‒ средняя скорость гравитационного осаждения м/с; tgid ‒ характерное время роста зародыша в процессе гидратации молекул воды; d0 ‒ окончательный диаметр капли; d ‒ начальный диаметр капли; ρ ‒ плотность воды; D ‒ молекулярный коэффициент диффузии молекул воды; p∞ ‒ давление водяных паров вдали от капли; S ‒ степень перенасыщения.
Для данного исследования была создана имитационная модель на базе программного комплекса, имитирующая действие существующего источника загрязнения – трубы высотой 107 метров медеплавильного завода города Карабаш Челябинской области. Моделирование производилось в предположении ровной подстилающей поверхности и в предположении поглощения загрязняющего вещества на высоте z = 0. Имитационная область моделирования 6000×6000×1000 метров, с разрешением матрицы клеточного автомата 60×60×10 метров на клетку. Поставленная задача может быть описана следующей системой дифференциальных уравнений:
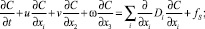
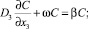 β = ∞, (7)
β = ∞, (7)
где C – концентрация примеси; t – время, прошедшее с момента выброса; u, v, ω – декартовые средние скорости сноса примеси; Di – вектор коэффициентов турбулентной диффузии, fS = f(x1, x2, x3, t) – функция, описывающая действие источников загрязнения; β – некоторая постоянная размерности скорости. Согласно последним данным, после внедрения ряда очистительных сооружений на медеплавильным заводе результирующая мощность выбросов пыли в атмосферу оценивается Q = 50 т/год [4].
Как показывают данные экспериментальных наблюдений, поле поверхностного загрязнения, полученное с помощью созданной имитационной модели [2, 5], верно характеризует реальную картину загрязнений на данной территории. В связи с этим возникла задача исследовать изменение результирующего поля поверхностного загрязнения в зависимости от входных параметров модели, а именно аппроксимации функции скорости ветра от времени.
Подробные данные о характерном состоянии атмосферы на высоте 121 м были получены сотрудниками обнинской метеорологической башни – уникального научного сооружения высотой 310 м. Экспериментальные данные скорости и направления ветра записываются каждый час и усредняются за 20-минутный промежуток времени, процесс сбора информации полностью автоматизирован. При анализе архивов экспериментальных данных за 10-дневный промежуток времени (с 02.02.2011 по 12.02.2011) была найдена функция распределения скорости и направления ветра рис. 1 а, б:
а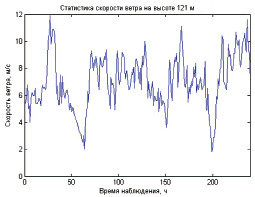 б
б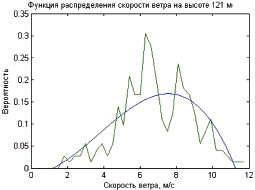
Рис. 1. Данные наблюдений, полученные с обнинской метеовышки:
а – подробные данные динамики поля скорости ветра; б – функция распределения вероятности скорости ветра на высоте. Экспериментальные данные аппроксимированы полиномом 3 степени
P(u) = –0,00082u3 + 0,00918u2 + 0,00133u – 0,01314. (8)
Хотя полученные данные по состоянию атмосферы территориально относятся к другой области, важно получить представление о характерном поведении скорости ветра на высоте порядка 100 метров. С другой стороны, рельеф местности обеих территорий принципиально не отличается, в связи с этим можно сделать предположение, что характерная вероятностная функция распределения скорости ветра на территории города Карабаш Челябинской области будет аналогична.
В качестве ожидаемого результирующего поля поверхностного загрязнения была принята картина, полученная в результате моделирования первой имитационной моделью рис. 2а при использовании подробных данных динамики изменения скорости ветра от времени (рис. 1а).
Как правило, при использовании стандартной Гауссовой модели рассеивания примесей от точечного источника скорость ветра принимают постоянной и равной среднестатистической скорости на исследуемой территории. В связи с этим вторая имитационная модель построена с учетом среднестатистической скорости ветра за 10-дневной промежуток (рис. 2б). Среднестатистическая скорость ветра составила 6,9 м/с. Относительное изменение суммарного уровня концентрации загрязняющего вещества на поверхности составило δ12 = 61,2 % (9) от ожидаемого (рис. 2а, в).
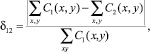 (9)
(9)
где C1, C2 ‒ расчетное распределение количества загрязняющего вещества, полученное в результате работы первой и второй имитационной модели соответственно. Аналогичная формула применялась для расчета δ13 полученного в результате работы первой и третьей имитационной модели.
Третья имитационная модель была построена на основе найденной вероятностной функции распределения скорости ветра (1) (рис. 1б). Результирующее поле поверхностного загрязнения представлено на рис. 3в. Относительное изменение суммарного уровня концентрации загрязняющего вещества на поверхности составило δ13 = 0б5 % (9) от ожидаемого (рис. 3а, б).
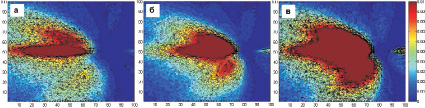
Рис. 2. Расчетные поля концентрации загрязняющего вещества.
Моделирование производилось на основе:
а – подробных данных о динамике скорости ветра; б – вероятностной функции скорости ветра; в ‒ постоянной скорости ветра. Концентрация представлена в кг/м2.,
Масштаб ‒ 60 метров на клетку
Согласно полученным результатам (рис. 2) флуктуации атмосферных параметров играют существенную роль при распространении загрязняющих веществ и формировании полей поверхностных загрязнений. Подробные метеорологические данные о состоянии атмосферы, как правило, не доступны для исследуемой территории, с другой стороны, накопленные архивные данные динамики атмосферных параметров исследуемой местности позволяют рассчитать статистические вероятностные функции.
Применение вероятностной функции динамики поля скорости ветра позволяет приблизиться к ожидаемому результату и относительное изменение суммарной концентрации загрязняющего вещества в этом случае составляет δ13 = 0,5 % от ожидаемого (9).
При использовании в модели средней скорости ветра относительное изменение суммарной концентрации загрязняющего вещества на подстилающей поверхности составило δ12 = 61,2 % от ожидаемого (9).
Работа выполнена при поддержке гранта «12-2-3-010-АРКТИКА» Методические основы и концепция интегральной системы управления качеством окружающей среды ЯНАО.
Рецензенты:
Никонов О.И., д.ф.-м.н., профессор, директор Департамента бизнес–информатики и математического моделирования Уральского федерального университета
им. первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Берг Д.Б., д.ф.-м.н., профессор кафедры анализа систем и принятия решений Уральского федерального университета
им. первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 26.10.2012.



