С тех пор как Ж. Ротштейном был обнаружен эффект влияния импульсного электрического поля на светочувствительность галогенсеребряных (AgHal) фотоматериалов прошло более 50 лет [10]. За это время состоялось как масштабное исследование «Эффекта Ротштейна» (преимущественно проведенное в бывшем СССР), так и его применение в научной фотографии для ядерно-физических экспериментов [3] и управления AgHal-фотографическим процессом [6, 7]. Недавние исследования взаимодействия барьерного разряда с AgHal-фотоматериалами показали, что «Эффект Ротштейна» реализуется и в этом случае, но в условиях не только однократного, но и многократного светового экспонирования [1, 2]. Несмотря на практическую привлекательность названного эффекта для программного управления чувствительностью различных фотографических систем, в настоящее время он пока не имеет какой-либо модели, адекватно описывающей кинетику процессов образования изображений и позволяющую предсказать наиболее подходящие условия его реализации на конкретных фоточувствительных материалах. Можно назвать лишь одну работу [9], посвященную этой проблеме. Однако авторы ограничились рассмотрением в ней только ионно-вакансионной стадии, т.е. без светового экспонирования фотоэмульсионных микрокристаллов (МК) AgHal. Поэтому в настоящей статье предлагается феноменологическая модель кинетики образования изображений на AgHal-фотоматериалах с учетом их светового экспонирования в импульсном электрическом поле с течением как ионно-вакансионных, так и электронно-дырочных процессов.
Постановка задачи. Для моделирования этих процессов решалась система одномерных кинетических уравнений непрерывности для концентраций катионов серебра Ag+ nAg, катионных вакансий nV, фотоэлектронов ne и фотодырок nh совместно с уравнением для напряженности электрического поля в МК AgHal Ek реальных фотографических эмульсий, предложенного в [4]:
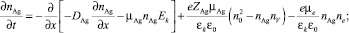 (1)
(1)
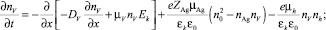 (2)
(2)
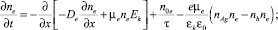 (3)
(3)
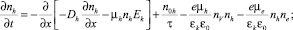 (4)
(4)
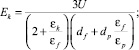 (5)
(5)
где 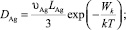
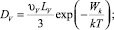
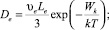
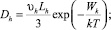
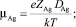
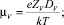
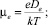
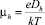 – диффузии и подвижности катионов Ag+, катионных вакансий V–, фотоэлектронов и фотодырок в МК AgHal с характерными длинами
– диффузии и подвижности катионов Ag+, катионных вакансий V–, фотоэлектронов и фотодырок в МК AgHal с характерными длинами 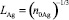 для Ag+ и вакансий
для Ag+ и вакансий 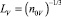 , а также эффективных длин пробега фотоэлектронов в МК
, а также эффективных длин пробега фотоэлектронов в МК 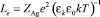 и фотодырок
и фотодырок 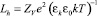 соответственно; ZAg и ZV – кратности зарядов Ag+ и V–, равных единице; n0Ag – начальная концентрация ионов Ag+, равновесно образующихся c катионными вакансиями V– концентрацией n0V, т.е.
соответственно; ZAg и ZV – кратности зарядов Ag+ и V–, равных единице; n0Ag – начальная концентрация ионов Ag+, равновесно образующихся c катионными вакансиями V– концентрацией n0V, т.е.
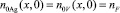
где 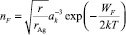 – концентрация дефектов Френкеля и энергия их образования WF = 1,7·10–19 – 1,09·10–18kT [9] в МК AgHal линейным размером (диаметром) r;
– концентрация дефектов Френкеля и энергия их образования WF = 1,7·10–19 – 1,09·10–18kT [9] в МК AgHal линейным размером (диаметром) r; 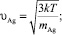
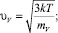
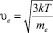 и
и 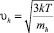 – скорости теплового движения ионов Ag+, V–, электронов и дырок соответственно;
– скорости теплового движения ионов Ag+, V–, электронов и дырок соответственно; 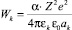 –
–
потенциальная энергия взаимодействия ионов кристаллической решетки AgHal;
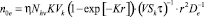
и –
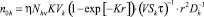
фотоэлектроны и фотодырки в МК AgHal объемом 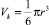 , сгенерированные световыми фотонами количеством Nhν за время τ на поверхности МК площадью Sk = 0,25πr2;
, сгенерированные световыми фотонами количеством Nhν за время τ на поверхности МК площадью Sk = 0,25πr2;
V – единичный объем (равный 1 м3); x – текущая координата; U – приложенное напряжение.
В ряде наших работ (например, в [1]) последний параметр являлся видеоимпульсом колоколообразной формы, подчиняющимся следующей эмпирически выведенной математической зависимости (вероятно, справедливой исключительно для использованного генератора высоковольтных импульсов):
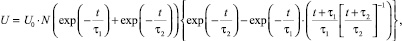 (6)
(6)
где U0 – начальное напряжение на электродах. На основании изложенного были определены соответствующие граничные условия задачи:
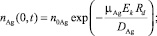
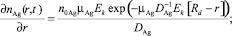 (7)
(7)
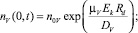
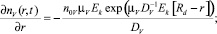 (8)
(8)
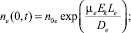
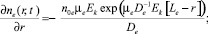 (9)
(9)
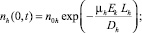
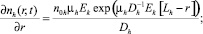 (10)
(10)
где 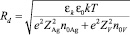 – Дебаевский радиус.
– Дебаевский радиус.
Для рационального решения системы (1)–(5) с начальными и граничными условиями (7)–(10) методом Рунге‒Кутта в ней было выполнено обезразмеривание уравнений. Численное моделирование осуществлялось на примере экспериментальных результатов по взаимодействию барьерного разряда с AgHal-фотоматериалами [1, 2] при вариантах напряженности электрического поля Ek = 5·106 В/м и Ek = 1,5·107 В/м, размерах МК AgHal исследованных фотопленок r = 3·10–7 м и r = 10–6 м, интенсивности светового излучения Jhν, создаваемого одиночной электронной лавиной ~3,4·105 квант/(м2·с). Расшифровка, обозначение и значения некоторых параметров для МК AgHal, а также физических постоянных, выбранных для расчета, приведены в таблице.
Результаты моделирования представлены на рис. 1–6 с совмещенной осциллограммой импульса напряжения, которая выделена сплошной линией черного цвета. Оси ординат на всех графиках представлены в безразмерных и относительных единицах, нормированных на N0 = n0Vk, а оси абсцисс – в единицах времени изменения импульса электрического поля Ek(t) (или длительности видеоимпульса приложенного напряжения t).
Как видно из рис. 1 и 2, в отсутствии освещения электрическое поле просто смещает ионы и вакансии, группируя их на противоположных сторонах кристалла AgHal в такт своего изменения. Причем более эффективно этот процесс реализуется для ионов Ag+ как имеющих наибольшую подвижность по сравнению с V–, остающихся почти неподвижными за все время изменения Ek. Описанные закономерности наблюдаются как для микро-, так и наноразмерных кристаллов AgHal при Ek = 5·106 В/м и Ek = 1,5·107 В/м, что согласуется с данными моделирования работы [9].
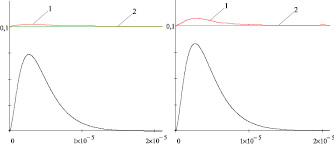
Рис. 1. Изменение концентраций ионов Ag+ (1) и ионных вакансий V– (2) в МК AgHal с r = 3·10–7 м под действием поля Ek = 5·106 В/м (слева) и Ek = 1,5·107 В/м (справа) в отсутствии освещения (описание в тексте)
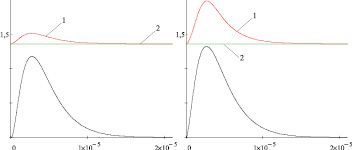
Рис. 2. Изменение концентраций ионов Ag+ (1) и ионных вакансий V– (2) в МК AgHal
с r = 10–6 м под действием поля Ek = 5·106 В/м (слева) и Ek = 1,5·107 В/м (справа)
в отсутствии освещения (описание в тексте)
Физические и геометрические значения некоторых параметров МК AgHal, фотографических слоев и постоянных, выбранных для численных расчетов
|
№ п/п |
Параметр и его обозначение |
Значение |
|
|
1 |
Элементарный электрический заряд, Кл |
e |
1,6021892∙10–19 |
|
2 |
Постоянная Больцмана, Дж/К |
k |
1,380658∙10–23 |
|
3 |
Стандартная температура, К |
T |
298 |
|
4 |
Диэлектрическая постоянная, Ф/м |
ε0 |
8,8541878∙10–12 |
|
5 |
Постоянная кристаллической решетки AgBr, м |
ak |
5,7748∙10–10 |
|
6 |
Постоянная Маделунга для кристалла AgBr |
α |
1,7476 |
|
7 |
Относительная диэлектрическая проницаемость МК AgBr |
εk |
12,5 |
|
8 |
Радиус ионов серебра, м |
rAg |
1,13∙10–10 |
|
9 |
Масса ионов серебра, кг |
mAg |
1,792∙10–25 |
|
10 |
Эффективная масса электрона, кг |
me |
1,1843∙10–32 |
|
11 |
Эффективная масса дырок, кг |
mh |
4,555∙10–30 |
|
12 |
Масса ионных вакансий в МК AgBr*, кг |
mV |
3,530∙10–21 |
|
13 |
Диэлектрическая проницаемость AgHal-фотоэмульсионного слоя |
εf |
5,89 |
|
14 |
Дэлектрическая проницаемость полимерной подложки |
εp |
3,23 |
|
15 |
Толщина фотоэмульсионного слоя AgHal-фотоматериала, м |
df |
5,70∙10–6 |
|
16 |
Толщина полимерной подложки AgHal-фотоматериала, м |
dp |
1,65∙10–4 |
|
17 |
Коэффициент поглощения фотонов кристаллом AgBr (для длины волны излучения λ = 400 нм), м–1 |
K |
105 |
|
18 |
Квантовый выход фотоэффекта в МК AgHal** |
η |
1 |
|
19 |
Длительность световой вспышки, с |
τ |
1,5·10–6 |
|
20 |
Длительность видеоимпульса напряжения, с |
t |
2,5·10–5 |
|
21 |
Длительность переднего фронта видеоимпульса напряжения, с |
τ1 |
2,5·10–6 |
|
22 |
Длительность заднего фронта видеоимпульса напряжения, с |
τ2 |
4,5·10–6 |
|
23 |
Подгоночный коэффициент |
N |
10,49 |
Примечания:
* рассчитано из данных в [9];
** значение для фотонов фиолетового и ультрафиолетового диапазонов электромагнитного спектра [5].
Кардинальные изменения концентраций всех заряженных частиц происходят в МК AgHal при их освещении, что видно из рис. 3–6. Кинетика для nAg, nV, ne и nh определяется как амплитудным значением напряженности поля в разноразмерных кристалликах Ek, так и скоростями его нарастания и спада. Наибольший интерес под влиянием этих факторов представляет поведение ионов Ag+ и фотоэлектронов, как основных частиц, образующих центры скрытого изображения (ЦСИ). На переднем и заднем фронтах электрополевого импульса наблюдаются резкие скачки их концентраций, соответствующие определенным, пороговым величинам Ek. До этого порога поле уменьшает или увеличивает концентрации частиц (в зависимости от знака их зарядов и направления поля), группируя их на противоположных сторонах МК. По мере нарастания Ek и достижения порогового уровня, при котором катионы и электроны набирают энергию, достаточную для их рекомбинации, начинает интенсивно осуществляться последний процесс. Он выражается сменой знака изменения nAg и ne в зависимости от вышеперечисленных параметров поля, а также размеров МК, и длится от ~0,1t до ~0,45t для Ag+ и от ~0,8t до ~0,95t для электронов.
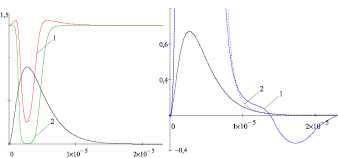
Рис. 3. Освещение МК AgHal c r = 10–6 м под действием электрического поля Ek = 5·106 В/м:
а – изменение концентраций ионов Ag+ (1) и ионных вакансий V– (2);
б – изменение концентраций электронов (1) и дырок (2) (описание в тексте)
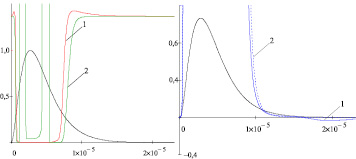
Рис. 4. Освещение МК AgHal c r = 10–6 м под действием электрического поля Ek = 1,5·107 В/м:
а – изменение концентраций ионов Ag+ (1) и ионных вакансий V– (2);
б – изменение концентраций электронов (1) и дырок (2) (описание в тексте)
Не менее интересно поведение вакансий. В отличие от варианта с неосвещенными МК размером 10–6 м под действием света и поля они подобно ионам Ag+ вовлекаются в интенсивную рекомбинацию с фотодырками. Данный процесс создает очень благоприятные условия для формирования серебряных ЦСИ, т.к. существенно уменьшает вероятность их разрушения за счет обратной рекомбинации фотоэлектронов с дырками и ионов Ag+ с вакансиями. Кроме того, как видно из рис. 4а и 6б, вакансионно-дырочная рекомбинация носит многоимпульсный характер, что связано с величиной Ek и размерами МК AgHal. Таким образом, упомянутый в [9] размерный эффект четко реализуется и в предлагаемой модели, ярко выражаясь для наиболее подвижных час-
тиц – дырок и электронов. Например, для последних в нанометровых кристаллах изменение на заднем фронте электрополевого импульса имеет колебательный характер с убывающей амплитудой (см. рис. 5б и 6б), что, вероятно, объясняется процессом периодической отдачи энергии электронами, приобретенной от поля, на взаимодействие с кристаллической решеткой и рекомбинацию с Ag+. Очевидно, этот процесс будет длиться до тех пор, пока Ek не достигнет величины, соответствующей порогу нарушения такого динамического равновесия, по-видимому, устанавливающегося в областях минимальной Ek. Поведение дырок и вакансий в наноразмерных МК также имеет характерные черты. При Ek = 5·106 В/м и Ek = 1,5·107 В/м концентрации последних практически не меняются (рис. 5а и 6а), тогда как в тех же полях между ними начинается рекомбинация, выражающаяся для дырок одноимпульсным режимом при Ek = 5·106 В/м (рис. 5б) и при
Ek = 1,5·107 В/м – двухимпульсным (рис. 6б). Из чего следует, что в кристаллах AgHal указанного масштаба при определенных Ek и характере его изменения возможно управление как электронно-ионным, так и вакансионно-дырочным взаимодействием. По-видимому, подобное управление осуществимо и для кристаллов AgHal микронного масштаба, но в полях с Ek < 5·106 В/м (при рассмотренной величине Jhν), что требует соответствующей экспериментальной проверки.
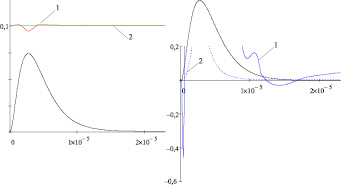
Рис. 5. Освещение МК AgHal c r = 3·10–7 м под действием электрического поля Ek = 5·106 В/м:
а – изменение концентраций ионов Ag+ (1) и ионных вакансий V– (2);
б – изменение концентраций электронов (1) и дырок (2) (описание в тексте)
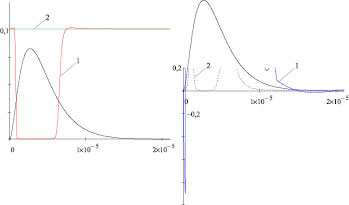
Рис. 6. Освещение МК AgHal c r = 3·10–7 м под действием электрического поля Ek = 1,5·107 В/м:
а – изменение концентраций ионов Ag+ (1) и ионных вакансий V– (2);
б – изменение концентраций электронов (1) и дырок (2) (описание в тексте)
Заключение
Несмотря на феноменологический подход в рассмотрении процессов образования изображений на AgHal-фотоматериалах под действием электрического поля, предложенная модель позволяет объяснить ряд известных экспериментальных результатов по «Эффекту Ротштейна», во многом считающихся аномальными и противоречивыми. Прежде всего, это относится к уменьшению светочувствительности у фотоматериалов с высоким значением этого параметра в поле Ek ~ 107 В/м и ее повышению у низкочувствительных фотоматериалов в поле той же напряженности [6]. Как показывает библиографический анализ, при рассмотрении этих процессов совершенно не уделялось внимание вакансионно-дырочному взаимодействию, которое, как оказалось, играет немаловажную роль в формировании ЦСИ и существенно зависящее от характера изменения и напряженности электрического поля в МК AgHal, а также их размеров. Как следует из результатов моделирования, именно в поле 1,5·107 В/м для МК рассмотренных размеров наблюдается сложный, многоимпульсный характер рекомбинации фотодырок с вакансиями, длящийся ~10–5 с, а каждый акт рекомбинаций – порядка (2–3)·10–6 с (зависящих от длительностей нарастания и спада электрополевого импульса). Аналогичный процесс взаимодействия протекает между фотоэлектронами и ионами Ag+, но в кристалликах нанометрового масштаба, как при Ek = 5·106 В/м, так и при Ek = 1,5·107 В/м. Из чего следует, что светочувствительность AgHal-фотографических слоев будет существенно зависеть от моментов возникновения световой вспышки на том или ином участке изменения импульса электрического поля Ek(t), что и наблюдается экспериментально [8]. Однако новый результат, выявленный при моделировании, – это упомянутый многоимпульсный характер рекомбинационных взаимодействий, указывающий на существенные изменения светочувствительности AgHal-фотоматериалов еще и при их многоимпульсном световом экспонировании с определенным периодом следования вспышек под действием одиночного импульса электрического поля, что обнаружено нами в [2].
Рецензенты:
Богатов Н.М., д.ф.-м.н., профессор, зав. кафедрой физики и информационных систем Кубанского государственного университета, г. Краснодар;
Копытов Г.Ф., д.ф.-м.н., профессор, зав. кафедрой радиофизики и нанотехнологий Кубанского государственного университета, г. Краснодар.
Работа поступила в редакцию 26.10.2012.



