Совершенствование элементной базы микроэлектроники, а также микросистемной техники позволяет, с одной стороны, существенно упростить мониторинг параметров движения человека за счет применения малоразмерных портативных датчиков, а с другой стороны, обеспечить большую детализацию мониторинга за счет увеличения числа датчиков, составляющих измерительную систему. Таким образом, поиск перспективных направлений дальнейшей миниатюризации инерциальных микроэлектромеханических систем (МЭМС) регистрации линейных ускорений и угловых скоростей, обеспечивающих мониторинг параметров движения человека, является актуальной научно-технической задачей, имеющей большое практическое значение [5].
Использование преобразователей перемещения на основе туннельного эффекта является одним из эффективных путей повышения чувствительности акселерометров. Под туннельным преобразователем перемещения понимается система, состоящая из подвижного и неподвижного электродов, разделенных пространственным зазором, величина которого составляет единицы нанометров и обеспечивает протекание туннельного тока между электродами, включенными во внешнюю цепь. Изменение взаимного расположения электродов обеспечивается передачей движения в МЭМС под действием внешних сил и приводит к изменению плотности туннельного тока в текущий момент времени [4].
В настоящей работе предлагается метод моделирования туннельных преобразователей перемещения МЭМС с нанометровыми пространственными зазорами посредством численного решения одномерного стационарного уравнения Шрёдингера.
Параметрическая модель туннельного преобразователя
На рис. 1 приведена геометрическая модель туннельного преобразователя перемещения МЭМС. Неподвижный и подвижный полупроводниковые электроды закреплены на изолирующей подложке и разделены пространственным зазором d. Перемещение подвижного электрода обеспечивается за счет упругой деформации подвеса, выполненного в виде консольной балки длины L, ширины w и толщины t. Ось чувствительности данного преобразователя проходит через центр симметрии неподвижного электрода и перпендикулярна плоскости подложки. Условимся считать неподвижный электрод эмиттером, а подвижный – коллектором.
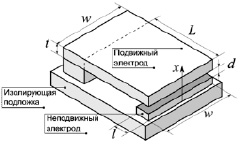
Рис. 1. Геометрическая модель туннельного преобразователя перемещения
В том случае, когда имеет место соотношение d ≪ l < w и можно пренебречь краевыми эффектами, потенциальный рельеф системы, приведённой на рис. 1, может быть представлен суперпозицией потенциальных энергий взаимодействия носителей заряда с поверхностями электродов, а также электростатическим полем в зазоре, обусловленным приложенной разностью потенциалов.
Рассмотрим систему, состоящую из одного электрода и свободного пространства. Принимая энергию электрона в вакууме и границу раздела электрод-вакуум за начало отсчета, потенциальный рельеф может быть выражен следующим образом [6]:
Us(x, φwf) = φwf∙(Θ(x) – 1), (1)
где φwf – работа выхода; Θ(x) – функция Хэвисайда.
Работа выхода определяется выражением [4]:
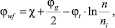(2)
где χ – сродство к электрону; φg– ширина запрещенной зоны; φt – температурный потенциал; n – концентрация электронов; ni – собственная концентрация.
В том случае, когда Us(x, φwf) < 0, частица считается связанной в твёрдом теле, в противном случае, Us(x, φwf) ≥ 0, частица считается свободной.
Потенциальный рельеф, соответствующий системе вакуум-электрод, по аналогии с (1) может быть представлен следующим образом:
U′s(x, φwf) = –φwf∙Θ(x). (3)
Выражение (3) описывает функцию, симметричную по отношению к (1).
Потенциальный рельеф преобразователя описывается выражением:
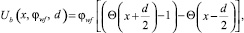(4)
где d – расстояние между электродами.
Чтобы учесть взаимодействие электрона с электростатическим полем, обусловленным приложенной разностью потенциалов, необходимо построить суперпозицию правой части уравнения (4), решения уравнения Лапласа в области, ограниченной поверхностями электродов, а также уравнения Пуассона в областях
электродов:
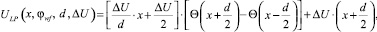(5)
где ΔU – разность потенциалов электрода-эмиттера (неподвижный электрод на рис. 1) и электрода-коллектора (подвижный электрод на рис. 1).
Чтобы учесть влияние взаимодействия между туннелирующим электроном и электродами необходимо модифицировать выражение (4):
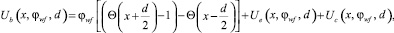(6)
где Ue(x, φwf, d) – поправочная функция, выражающая взаимодействие электрона с поверхностью эмиттера; Uc(x, φwf, d) – поправочная функция, выражающая взаимодействие электрона с поверхностью коллектора.
Поправочные функции Ue(x, φwf, d) и Uc(x, φwf, d) имеют вид:
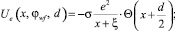(7)
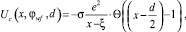(8)
где ξ – параметр, определяемый из соотношения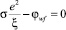 
и характеризующий протяженность поверхностного слоя, в котором электрон ещё считается связанным в твердом теле; 
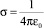– коэффициент для системы физических величин (СИ).
Потенциальный рельеф преобразователя теперь может быть представлен в виде:
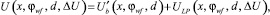(9)
где Ub(x, φwf, d) выражает взаимодействие электрона с поверхностями электродов, а ULP(x, φwf, d, ΔU) – с полем в зазоре, обусловленным разностью потенциалов ΔU.
Параметрами разработанной модели являются: работа выхода φwf, расстояние между электродами, а также разность потенциалов ΔU. На рис. 2 приведен график функции U(x), полученной из (9) после спецификации параметров.
Моделирование туннельного эффекта в преобразователе перемещения
Известно, что плотность туннельного тока через наноразмерную структуру, может быть выражена следующим образом [1]:
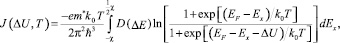(10)
где k0 – постоянная Больцмана; T – абсолютная температура; e – заряд электрона; m* – эффективная масса электрона; ħ – приведенная постоянная Планка; EF – уровень Ферми; Ex – кинетическая энергия, связанная с движением электрона вдоль оси x; ΔU – приложенная разность потенциалов; D(ΔE) – коэффициент прозрачности; ΔE – разность между текущим и минимальным разрешенным значением полной энергии носителей заряда; χ – сродство к электрону.
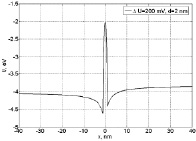
Рис. 2. Потенциальный рельеф туннельного преобразователя перемещения
На основании соотношения неопределенностей Гейзенберга для энергии и времени ΔE·Δt ≥ ħ инерционность процесса туннелирования электронов с неопределенностью по энергии порядка единиц электронвольт характеризуется временами порядка 10–15 c. Поскольку изменение потенциальной энергии системы электродов преобразователя, обусловленное изменением конфигурации электродов, происходит за время порядка 10–5 c, движение носителей заряда в системе электродов преобразователя может быть описано стационарным уравнением Шрёдингера [6]. Если принять величину ΔU нормировочным множителем для
потенциальной энергии, а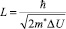 
– нормировочным множителем для координаты, то уравнение Шрёдингера после нормировки может быть записано в виде:
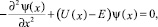(11)
где ψ(x) – нормированная волновая функция; x – нормированная координата;
U(x) – нормированная потенциальная энергия; E – нормированная полная энергия
частицы.
Аналитическое решение уравнения (11) возможно построить лишь в случае, когда потенциальный рельеф U(x) задан на множестве последовательных отрезков, на каждом из которых значение потенциальной энергии постоянно. Известно, что уже в случае потенциального барьера треугольной формы коэффициент прозрачности вычисляется приближенно [7].
Численный метод расчета коэффициента прозрачности потенциального барьера
Предлагаемый метод основывается на следующих допущениях:
– для описания движения частицы в области электродов применяется приближение эффективной массы, что позволяет использовать потенциальные рельефы вида (9);
– спектр оператора полной энергии принимается непрерывным и ограничивается сверху, что позволяет, с одной стороны, не учитывать влияния связанных состояний на движущуюся частицу, а с другой – упростить расчет плотности тока численными методами;
– взаимодействие волновой функции движущейся частицы и потенциального барьера не изменяет форму потенциального рельефа, что позволяет не учитывать влияния зарядовой плотности туннелирующих частиц.
Дискретизация уравнения (11) производится на сетке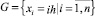 
. Заменяя в уравнении производные конечными разностями соответствующих порядков, получим:
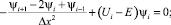(12)
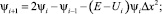(13)
где ψi = ψ(G) и Ui = U(G) – значения сеточных функций в точках сетки; Δx – шаг сетки.
Решение уравнения (12) для рассеянной частицы в соответствии с определенными ранее допущениями можно представить в виде:
ψi = exp(κixi + δ), (14)
где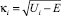 
– волновое число, определяемое потенциальным рельефом; δ – приращение фазы, обусловленное рассеянием.
Для инициализации вычислительной схемы (13) необходимо задать значения сеточной функции ψi в двух точках сетки x1, x2. Следует отметить, что начальная фаза выбрана так, чтобы амплитуда рассеянной волны в выражении (14) была равна единице.
Условие непрерывности и непрерывной дифференцируемости волновой функции в каждой точке сетки (непрерывности логарифмической производной) однозначно определяет ее значение в последующей точке.
Предполагая, что частица движется справа налево, имеем из условия непрерывности логарифмической производной в точке x1:
ψ2 = (1 + κ1 Δx) ψ1, (15)
где κ1 – волновое число, соответствующее координате x1, ψ1, ψ2 – численные значения волновой функции в соответствующих точках сетки.
Поскольку решения однородных уравнений вида (11) определены с точностью до постоянного фазового множителя [7], значение ψ1 может быть выбрано произвольно, а ψ2 однозначно определяется выражением (15).
Из условия непрерывности логарифмической производной в точке xn следует:
A∙exp(–κn xn) + R∙exp(κn xn) = ψn, (16)
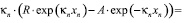
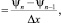(17)
где xn – точка, соответствующая правой границе области решения; κn – волновое число в точке xn; A – амплитуда падающей волны; R – амплитуда отраженной волны.
Уравнения (16) и (17) образуют совместную систему, решая которую, можно получить амплитуды отраженной и падающей волн:
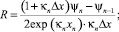(18)
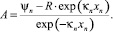(19)
По определению, коэффициентом прозрачности потенциального барьера T называют отношение квадратов модулей амплитуд прошедшей и падающей волн [7]. Отношение квадратов модулей амплитуд отраженной (18) и падающей (19) волн называют коэффициентом отражения M. Амплитуда прошедшей волны в рассмотренной вычислительной схеме фактически считается известной, поэтому для определения T используется свойство, выражающее закон сохранения потока частиц T + M = 1:
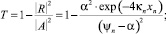(20)
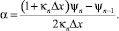(21)
Таким образом, для того чтобы рассчитать коэффициент прозрачности по формулам (20), (21), необходимо вычислить значения волновой функции в последней и предпоследней точках сетки.
Заключение
Основными отличительными особенностями предложенного метода моделирования туннельных преобразователей перемещения МЭМС являются:
– использование параметрической модели туннельного преобразователя;
– учет взаимодействия туннелирующих электронов с электродами преобразователя;
– численный расчет коэффициентов прозрачности потенциальных рельефов.
Кроме того, разработанный метод может быть использован для моделирования квантового транспорта в сверхрешетках и подобных им функциональных наноструктурах [3].
Проведенное сравнение результатов, полученных предложенным методом, с результатами аналитического решения уравнения (11) на барьерах вида (4) показало, что относительная погрешность определения коэффициента прозрачности T, для которых известно точное аналитическое решение, по равномерной норме составляет менее 2 %.
Следует также отметить, что значения коэффициентов прозрачности T потенциальных рельефов вида (9), полученных с помощью описанного метода, существенно (в отдельных случаях до 60 % по равномерной норме) отличаются от рассчитанных по известным формулам квазиклассического приближения, не учитывающим взаимодействия туннелирующих электронов с электродами преобразователя, что свидетельствует о неправомерности использования квазиклассических моделей туннельных преобразователей перемещения с наноразмерными пространственными зазорами.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (Гос. соглашение № 14.А18.21.0126) в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Рындин Е.А., д.т.н., профессор, ведущий научный сотрудник ЮНЦ РАН;
Жорник А.И., д.ф.-м.н., профессор кафедры теоретической, общей физики и технологии ФГБОУ ВПО ТГПИ.
Работа поступила в редакцию 26.10.2012.