Методы неразрушающего контроля (НК) основаны на регистрации изменений физических параметров материала, из которого изготовлен диагностируемый элемент конструкции или деталь, вследствие воздействия на него неблагоприятных внешних факторов. Расширение спектра методов НК, таким образом, должно производиться за счет исследования новых физических явлений в различных материалах, возникающих при деформировании.
Многообещающими в этом отношении являются механолюминесцентные материалы. Анализ литературы по данной тематике показывает недостаточное число прикладных исследований механолюминесцентных материалов с целью разработки методов НК, в то время как в работах
[5, 6, 8, 9] обозначается перспективность данного направления.
Построение математических моделей излучения для различных механолюминесцентных материалов, а также определение закономерностей формирования выходных оптических сигналов чувствительных элементов на основе механолюминесцентных материалов в зависимости от входных воздействий, вызывающих дефекты, являются необходимыми этапами разработки соответствующих систем мониторинга дефектов.
Математическая модель
механических напряжений
Приведенная в работе [8] математическая модель механолюминесцентного внутрицентрового излучения цинксульфидных порошковых люминофоров не всегда может быть применена при разработке систем мониторинга, поскольку содержит большое количество несправочных величин и связывает поток излучения при механолюминесценции только с деформационными напряжениями в материале. В то же время экспериментально механолюминесценция, как правило, генерируется путем воздействия на материал лазерного импульса малой длительности (10–6–10–3 с) и радиуса [1, 4, 7] и, следовательно, величина напряжения в материале не следует явно из экспериментальных данных. Таким образом, разработка математической модели, связывающей величины механических напряжений в материале с параметрами инициирующего лазерного импульса, является актуальной задачей.
Для решения этой задачи в данной работе предложена модель, включающая нестационарное уравнение теплопроводности, описывающее распределение температуры в объекте исследования под воздействием лазерного импульса, и уравнения термоупругости [3], позволяющие определить механические напряжения, возникающие вследствие теплового воздействия:
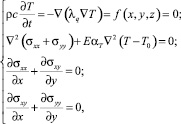
(1)
(2)
(3)
(4)
где ρ – плотность материала; c – удельная теплоемкость; λq – коэффициент теплопроводности; T – абсолютная температура; t – время; x, y, z – координаты; f(x, y, z) – функция плотности мощности источников тепла; E – модуль Юнга; αТ – коэффициент линейного теплового расширения; σxx, σxy, σyy – компоненты тензора напряжения;
Т0 – начальная температура тела.
Уравнения (1)–(4) решались для граничных условий:
 (5)
(5)
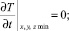 (6)
(6)
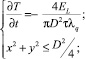 (7)
(7)
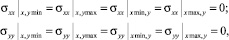 (8)
(8)
где D – диаметр лазерного пучка в месте его падения на пластину; ЕL – энергия лазерного импульса; τ – длительность лазерного импульса.
Лазерный импульс воздействует на малую площадь поверхности тела S = πD2/4 (рис. 1).
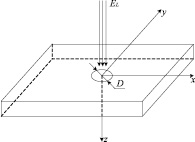
Рис. 1. Область воздействия лазерного импульса
В случае равномерного распределения плотности мощности по площади сечения лазерного луча задаются граничные условия второго рода (7).
Распределение интенсивности лазерного импульса в пучке, как правило, соответствует нормальному закону распределения Гаусса [2]. Для лучшей корреляции с экспериментальными данными следует задать для области воздействия лазерного импульса следующие граничные условия второго рода:
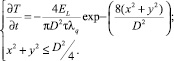 (9)
(9)
В общем случае задачи тепропроводности и термоупругости решаются для трех измерений, но с учетом того, что объектом исследования является тонкая пленка или пластина, целесообразно решать задачу термоупругости для двух измерений (x, y), а уравнение теплопроводности для трех измерений с последующим преобразованием в двумерное распределение температуры в соответствии с выражением:
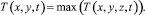 (10)
(10)
Задача распределения температуры в пластине решается в трех измерениях, поскольку для двух измерений тепловой поток лазерного излучения может быть задан лишь как эквивалентный внутренний источник тепла, что может оказаться некорректным. Полученные в результате решения уравнения теплопроводности нестационарные распределения температуры использовались для последующего решения уравнения термоупругости.
Система (1)–(10) решалась численно с использованием метода конечных разностей.
Учет в граничных условиях задачи процессов конвекции и лучистого обмена не составляет значительной вычислительной сложности, однако в данной работе эти процессы не учитывались исходя из следующих соображений:
• для изучения процесса механолюминесценции существенное значение имеют напряженные состояния на малом отрезке времени, недостаточном для релаксации материала, и, следовательно, потери тепла за счет конвективного теплообмена не будут заметно влиять на погрешность решения;
• значительному нагреву подвергается слишком малая площадь поверхности материала, чтобы потери тепла посредством лучистого обмена заметно повлияли на погрешность решения на рассматриваемом малом отрезке времени.
По результатам проведенных вычислений непосредственное решение системы уравнений (1)–(10) приводит к неадекватным результатам вне зависимости от метода дискретизации уравнений первого порядка (3) и (4). С целью решения данной проблемы уравнения (3) и (4) системы (1)–(10) были приведены посредством дополнительного дифференцирования к виду:
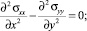 (11)
(11)
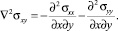 (12)
(12)
Численное решение системы уравнений (1), (2), (5)–(12) выполнялось для исходных данных, соответствующих сульфиду цинка, обладающему механолюминесцентными свойствами.
Результаты моделирования
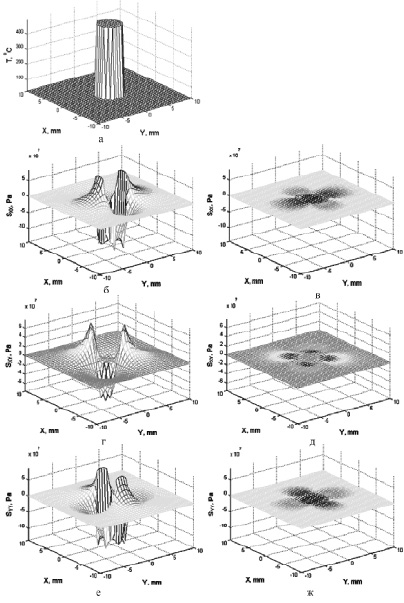
Рис. 2. Распределение по координатам температуры и напряжений на поверхности пластины
для равномерного распределения плотности мощности по площади сечения лазерного луча:
а – распределение температуры в момент прекращения действия лазерного импульса;
б, г, е – распределение напряжений σxx, σxy, σxz в пластине в момент прекращения действия лазерного импульса соответственно; в, д, ж – распределение напряжений в σxx, σxy, σxz пластине спустя 1 мс после прекращения действия лазерного импульса соответственно
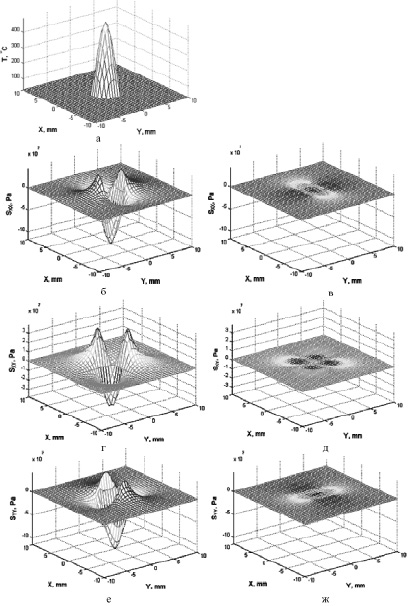
Рис. 3. Распределение по координатам температуры и напряжений на поверхности пластины для гауссовского распределения плотности мощности по площади сечения лазерного луча:
а – распределение температуры в момент прекращения действия лазерного импульса;
б, г, е – распределение напряжений σxx, σxy, σxz в пластине в момент прекращения действия лазерного импульса соответственно; в, д, ж – распределение напряжений в σxx, σxy, σxz пластине спустя 1 мс после прекращения действия лазерного импульса соответственно
На рис. 2–3 приведены распределения по координатам температур и компонент тензора напряжений σxx, σxy, σyy в различные моменты времени, полученные из решения системы (1), (2), (5)–(12) при длительности лазерных импульсов 1 мс для равномерного и гауссовского распределений плотности мощности по площади сечения лазерного луча.
Заключение
Разработанная модель позволяет получить нестационарные распределения температур и компонент тензора механических напряжений в зависимости от параметров лазерных импульсов, что обеспечит эффективное применение экспериментальных данных для разработки систем мониторинга дефектов на основе явления механолюминесценции.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (Гос. контракт № 16.740.11.0425 от 03.12.2010, гос. соглашение № 14.А18.21.0126) в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Агеев О.А., д.т.н., профессор, директор НОЦ «Нанотехнологии»;
Жорник А.И., д.ф.-м.н., профессор кафедры теоретической, общей физики и технологии ФГБОУ ВПО ТГПИ.
Работа поступила в редакцию 26.10.2012.



