Оптоэлектроника как научно-техническое направление предполагает развитие целого ряда базовых технологий и главным образом технологии создания новых типов высокоэффективных полупроводниковых материалов и структур на их основе, включая квантово-размерные структуры [5, 6].
Метод построения модулируемых источников оптического излучения
Одним из наиболее перспективных путей построения сложных быстродействующих систем мониторинга и анализа информации в настоящее время является создание гибридных УБИС: отдельные ядра на кристалле, содержащие схемы обработки электронных сигналов, изготавливаются на основе кремния, а системы оптической коммутации ядер формируются на основе полупроводниковых соединений типа AIIIBV и функционально интегрируются с кремниевыми ядрами в едином технологическом процессе, что обеспечивает интеграцию оптоэлектронного интерфейса для соединений между компонентами УБИС. Кроме того, оптоэлектронные компоненты могут использоваться для получения, преобразования и передачи информации непосредственно внутри систем.
Инжекционные лазеры являются важнейшими элементами интегральных оптоэлектронных информационно-измерительных систем мониторинга. В данной работе описывается структура функционально интегрированного лазера-модулятора, обеспечивающего внутреннюю амплитудную модуляцию оптического излучения. Это устройство имеет ряд преимуществ, в частности, позволяет отказаться от использования модуляторов как отдельных устройств, кроме того, описываемые устройства значительно превосходят лазеры с модуляцией посредством управления плотностью тока накачки по быстродействию [2].
Учитывая масштабность современных исследований, направленных на создание различных по назначению систем терагерцового диапазона (в том числе и интегральных систем оптической коммутации компонентов систем мониторинга и обработки информации), повышение максимальной частоты амплитудной модуляции излучения, генерируемого интегральными инжекционными лазерами, является актуальной проблемой.
В работах [7, 9, 11] представлены результаты разработки и исследования интегральных логических элементов и коммутаторов с управляемой передислокацией максимума амплитуды волновых функций носителей заряда в связанных квантовых областях с взаимодополняющими типами проводимости на основе гетероструктур материалов группы AIIIBV. Показано, что использование методов зонной инженерии, принципа управляемой передислокации максимума амплитуды волновых функций носителей заряда в сочетании с принципами комплементарной логики обеспечивает сокращение минимального времени задержки интегральных элементов до значений менее 0,2 пс.
В данной работе исследуется возможность создания на основе перечисленных принципов интегральных инжекционных лазеров с функционально интегрированными амплитудными модуляторами, обеспечивающими модуляцию стимулированного излучения в терагерцовом диапазоне частот для оптической коммутации компонентов систем мониторинга и обработки информации. Областью применения таких инжекционных лазеров являются интегральные системы оптической коммутации многоядерных УБИС, телекоммуникационные и вычислительные системы, средства связи, высокочувствительные системы медицинской диагностики, системы регистрации и анализа быстропротекающих физических процессов и др.
Основными требованиями, предъявляемыми к модуляторам лазерного излучения интегральных систем оптической коммутации компонентов систем мониторинга, являются высокое быстродействие (соответствующее гигагерцовому, а в ближайшей перспективе –
терагерцовому диапазону частот) и возможность изготовления в едином технологическом цикле с инжекционными лазерами и остальными компонентами систем мониторинга.
Модель
функционально-интегрированных лазеров-модуляторов
Традиционно динамику функционирования инжекционных лазеров описывают уравнениями кинетики, представляющими собой систему обыкновенных дифференциальных уравнений. Эта модель не позволяет учесть влияние пространственного распределения концентраций подвижных носителей заряда и фотонов в активной области лазера на интенсивность генерируемого стимулированного излучения [1, 4].
Учет данного фактора может быть осуществлен в процессе численного решения фундаментальной системы уравнений (ФСУ) полупроводника в диффузионно-дрейфовом приближении, однако в этом случае не учитывается влияние фотонов лазерной моды на распределение концентраций подвижных носителей, скорость излучательной рекомбинации и, как следствие, на интенсивность генерируемого излучения [3].
Особенность структуры предложенного устройства состоит в том, что в отличие от традиционных инжекционных лазеров предусмотрены два дополнительных управляющих контакта, создающих в активной области лазера-модулятора поперечное управляющее поле.
Для решения задачи моделирования инжекционных лазеров-модуляторов в данной работе используется комплексная модель, учитывающая влияние пространственного распределения концентраций электронов, дырок и фотонов в активной области лазера на интенсивность генерируемого стимулированного излучения. Разработанная модель в векторной форме в базисе переменных
{n, p, j, f} для двух пространственных измерений может быть записана следующим образом:
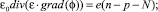 (1)
(1)
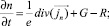 (2)
(2)
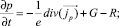 (3)
(3)
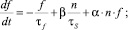 (4)
(4)
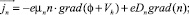 (5)
(5)
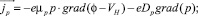 (6)
(6)
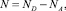 (7)
(7)
где e0 – электрическая постоянная; e – диэлектрическая проницаемость полупроводника; j – электростатический потенциал; e – электростатический потенциал; n – концентрация электронов; p – концентрация дырок; N – эффективная концентрация примесей; t – время протекания процессов в активной области лазера; jn – электронная составляющая плотности тока; jp – дырочная составляющая плотности тока; G – скорость генерации электронно-дырочных пар в активной области; R – скорость рекомбинации электронно-дырочных пар в активной области; f – плотность фотонов в лазерной моде; τf – время жизни фотона в резонаторе; tS – время спонтанной излучательной рекомбинации; α – коэффициент оптического усиления; β – доля спонтанного излучения, попадающего в лазерную моду; mn – подвижность электронов; mp – подвижность дырок; Vh – гетероструктурный потенциал в области зоны проводимости; VH – гетероструктурный потенциал в области валентной зоны; Dn – коэффициент диффузии электронов; Dp – коэффициент диффузии дырок; ND – концентрация доноров; NA – концентрация акцепторов.
Граничные условия на металлических контактах принимаются в соответствии с условиями Дирихле на свободных поверхностях гетероструктуры – Неймана.
Начальные условия определяются по результатам решения соответствующей стационарной задачи.
В виду того, что предложенная модель не учитывает квантовых эффектов в активной области структуры лазера-модулятора, была разработана методика численного моделирования, предполагающая на одном из этапов оценку быстродействия моделируемого элемента посредством численного решения нестационарного уравнения Шредингера. Основные этапы предложенной методики моделирования могут быть сформулированы следующим образом:
– на начальных этапах решается нестационарное уравнение Шредингера с целью оценки быстродействия системы с учетом квантовых эффектов. Для получения начального условия выполняется самосогласованное решение стационарного уравнения Шредингера и уравнения Пуассона;
– для получения начального приближения к решению разработанной комплексной модели выполняется численное решение ФСУ полупроводника в диффузионно-дрейфовом приближении в базисе «потенциал, экспоненты квазиуровней Ферми для электронов и дырок» методом конечных разностей с использованием итерационной схемы Гуммеля в сочетании с методом продолжения решения по параметру (параметром является напряжение питания лазера);
– с использованием полученного начального приближения выполняется численное решение разработанной комплексной модели с учетом пространственного распределения концентраций электронов, дырок и фотонов методом Ньютона‒Рафсона в сочетании с методом продолжения решения по параметру (параметром является управляющее напряжение);
– применение метода продолжения решения по параметру позволяет эффективно решить проблему начального приближения при моделировании режима высокого уровня инжекции, характерного для моделируемых лазеров-модуляторов, и повысить скорость сходимости вычислительного процесса [8, 10].
На основе предложенных моделей и методики моделирования разработаны программные средства численного моделирования функционально интегрированных лазеров-модуляторов. Отдельные результаты численного моделирования представлены на рис. 1–3.
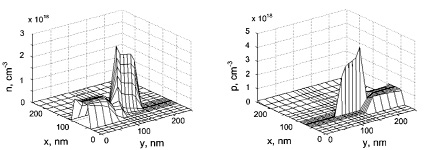
Рис. 1. Распределение концентрации электронов и дырок по координатам в лазере-модуляторе в режиме лазерной генерации;
а – распределение концентрации электронов по координатам;
б – распределение концентрации дырок по координатам
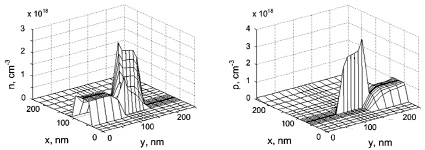
Рис. 2. Распределение концентрации электронов и дырок по координатам в лазере-модуляторе в отсутствие лазерной генерации:
а – распределение концентрации электронов по координатам;
б – распределение концентрации дырок по координатам
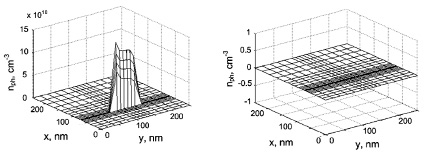
Рис. 3. Распределения концентрации фотонов по координатам в лазере-модуляторе в режиме лазерной генерации:
а – в режиме лазерной генерации; б – в отсутствие лазерной генерации
В соответствии с полученными результатами численного решения уравнений разработанной модели управляемая поперечным электрическим полем передислокация максимумов плотности электронов и дырок в пространственно смещенных квантовых областях лазера-модулятора обеспечивает амплитудную модуляцию стимулированного излучения с коэффициентом, превышающим 0,9 при неизменном токе по цепи питания лазера.
По результатам численного решения уравнения Шредингера показано, что время управляемой передислокации максимума амплитуды волновых функций носителей заряда в квантовых областях составляет (0,09–0,13) пс в зависимости от ширины данных областей. Таким образом, максимальная частота амплитудной модуляции стимулированного излучения в рассматриваемых интегральных системах оптической коммутации может достигать единиц ТГц.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (Гос. контракт № 16.740.11.0425 от 03.12.2010, гос. соглашение № 14.А18.21.0126) в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы.
Рецензенты:
Агеев О.А., д.т.н., профессор, директор НОЦ «Нанотехнологии»;
Жорник А.И., д.ф.-м.н., профессор кафедры теоретической, общей физики и технологии ФГБОУ ВПО ТГПИ.
Работа поступила в редакцию 26.10.2012.



