Как известно, интерес школьников к математике и соответственно качество математических знаний учащихся в настоящее время резко падает. Это отмечается в многочисленных публикациях и выступлениях, как известных ученых, так и учителей-практиков. Об этом свидетельствуют и факт снижения конкурсов абитуриентов на физико-математические факультеты вузов нашей страны, и результаты международных олимпиад, а также невысокие результаты российских учащихся в исследовании международных тестов PISA и др. (по результатам исследования математической грамотности 15-летних учащихся в 2009 году российские учащиеся оказались в группе стран, результаты которых существенно ниже результатов стран ОЭСР. Средний балл российских учащихся составил 468 баллов, по странам ОЭСР – 496, что соответствует 38–40 местам среди 65 стран-участниц) [5].
В то же время ведется поиск решения этой проблемы с учетом современных реалий. Одним из средств повышения эффективности образовательного процесса, в том числе и математического образования школьников, предлагаются информационные компьютерные технологии, среди них важное место занимают электронные учебники и учебные пособия (ЭУП). Специалисты [2, 4, 7, 9] отмечают ряд возможных преимуществ ЭУП перед печатными изданиями, а именно они:
– допускают адаптацию в соответствии с потребностями учащегося, уровнем его подготовки, интеллектуальными возможностями и амбициями;
– освобождают от громоздких вычислений и преобразований, позволяя сосредоточиться на сути предмета, рассмотреть большее количество примеров и решить больше задач;
– для проверки усвоения учебного материала предлагают интерактивные задания для самостоятельной работы учеников;
– предоставляют широчайшие возможности для самопроверки на всех этапах
работы;
– обеспечивают удобство графического интерфейса учебника в использовании;
– дают возможность красиво и аккуратно оформить работу и сдать ее преподавателю в виде электронного файла или распечатанного текста;
– выполняют роль бесконечно терпеливого наставника, предоставляя практически неограниченное количество разъяснений, повторений, подсказок и т.д.
Наше исследование связано с использованием ЭУП для решения проблемы повышения эффективности обучения математике детей с особыми образовательными потребностями.
Ребенок с особыми образовательными потребностями (потребностями в образовании) – это вновь возникший и еще не устоявшийся термин, который возникает во всех странах мира при переходе от унитарного к открытому гражданскому обществу, когда оно осознает необходимость отразить в языке свое меняющееся отношение к детям с нарушениями в развитии, новое понимание их прав.
Содержание термина «дети с особыми образовательными потребностями» органично отражает традиционное для отечественной дефектологии понимание ребенка с нарушениями в развитии как нуждающегося в «обходных путях» достижения тех задач культурного развития, которые в условиях нормы достигаются укоренившимися в культуре способами воспитания и принятыми в обществе способами массового образования.
Рассмотрим некоторые статистические данные. По степени распространенности в пределах детской возрастной группы первое место по численности занимают дети с образовательными затруднениями (более 40 %), второе место – с нарушениями интеллекта (более 20 %), третье – с нарушениями речи (около 20 %), остальные нарушения в совокупности составляют менее 20 %. По данным НИИ гигиены и охраны здоровья детей и здоровья Научного центра здоровья детей РАМН за последнее время число здоровых дошкольников уменьшилось в пять раз и составляет лишь около 10 % среди контингента детей, поступающих в школу. Распространенность функциональных отклонений достигает более 70 %, хронических заболеваний – 50 %, физиологической незрелости – 60 %, более 20 % детей имеют дефицит массы тела.
В коррекционной педагогике [1, с. 11] выделяются различные категории детей с отклонениями в развитии. К их числу относятся дети:
– с нарушениями одного из анализаторов: с полной (тотальной) или частичной (парциональной) потерей слуха или зрения, неслышащие (глухие), слабослышащие или, как их раньше назвали, тугоухие;
– незрячие (слепые), слабовидящие;
– со специфическими речевыми отклонениями (алалия, общее недоразвитие речи, заикание);
– с нарушениями опорно-двигательного аппарата (церебральный паралич, последствия травм позвоночника или перенесенного полиомиелита);
– умственно отсталые и с различной степенью выраженности задержки психического развития (разные формы психического недоразвития с преимущественной несформированностью интеллектуальной деятельности);
– со сложными нарушениями (незрячие умственно отсталые; слепоглухие, слепоглухие с умственной отсталостью, слепые с нарушениями речи и др.);
– аутичные (активно избегающие общения с окружающими людьми).
Таким образом, понятие «ребенок с особыми образовательными потребностями» предполагает наличие серьезных отклонений в развитии, вызванных болезнетворными влияниями, которые обуславливают необходимость создания специальных условий для обучения и воспитания. Важно иметь возможность задействовать у пользователя все его каналы восприятия информации: зрение, слух, подсознание и т.д. Как показало наше исследование (еще на зондирующем этапе), ЭУП позволяет не только повышать качество обучения за счет интеграции всех своих психофизических усилий, но и косвенно развивать способность к целостному комплексному восприятию мира.
Не имея возможности в рамках одного исследования охватить все перечисленные выше группы детей, в формирующий эксперимент по обучению математике с использованием специально составленного ЭУП нами выбраны дети с нарушениями опорно-двигательного аппарата. При разработке ЭУП мы исходили из следующего его определения: «Электронное учебное пособие – это электронное издание, частично или полностью заменяющее или дополняющее учебник и официально утвержденное в качестве данного вида издания» [4, с. 20]. При этом в качестве основных принципов ЭУП отмечается дозированность учебного материала, активная самостоятельная работа
обучаемого, постоянный контроль усвоения учебного материала, индивидуализация темпа обучения, большой объем учебного материала, возможность интерактивной обратной связи.
Разработанная нами и использованная в формирующем эксперименте серия ЭУП для изучения курса алгебры в 8-м классе реализована в системе визуального программирования Delphi 7. Каждое ЭУП представляет собой многооконное Windows-приложение. Сама по себе программа не требует специальной установки. Нужно только скопировать рабочую папку программы на логический диск или в другую папку, где будет лежать программа. ЭУП запускается файлом «Учебник.exe». Для полного функционирования ЭУП необходимо наличие в операционной системе Microsoft Equation 3.0, MS Power Point и Microsoft Word.
Не имея возможности в рамках настоящей статьи описать всю серию ЭУП, проиллюстрируем их структуру и особенности на примере одного из пособий, посвященного квадратным уравнениям (рис. 1). Содержание ЭУП «Квадратные уравнения» (электронное учебное пособие зарегистрировано в ОФЕРНИО [8]) подразделяется на 6 тем (рис. 2). Кроме тематических ссылок, эта форма содержит только две кнопки: «Выход» – для завершения работы с учебным пособием, и «Сведения об авторах» –
отображает дополнительное диалоговое окно. Наводя мышкой на соответствующую строчку в содержании, ученик может выбрать нужную тему, то есть чтение учебного пособия не обязательно должно быть последовательным.

Рис. 1. Вид обложки электронного учебного пособия «Квадратные уравнения»

Рис. 2. Содержание электронного учебного пособия «Квадратные уравнения»
Выбрав нужную тему, пользователь попадает на основную форму ЭУП (рис. 3, 4), рабочая область которой в зависимости от выбранной темы и режима использования («теория», «решение задач», «игра») имеет различное содержание.

Рис. 3. Фрагмент изложения темы «Дело об определении квадратного уравнения»

Рис. 4. Продолжение фрагмента изложения темы «Дело об определении квадратного уравнения»
Поскольку в обучении учеников с особыми образовательными потребностями большая доля отводится самостоятельной работе, то при построении математического содержания мы исходили из того, что использовать в обучении традиционные учебники неэффективно, так как они написаны конспективно, лаконично и не вызывают у ученика желание добровольно в свободное время его читать и изучать математический материал. В составленном нами варианте серии ЭУП использованы основные принципиальные положения учебников томской группы педагогов МПИ проекта под руководством доктора пед. наук, профессора Эмануилы Григорьевны Гельфман, в частности, включение математического текста в занимательные сюжеты. Так, к примеру, при построении ЭУП «Квадратные уравнения» для учащихся 8 класса использовались сюжеты с участием мистера Шерлока Холмса и доктора Уотсона по аналогии с тем, как это было сделано в учебном пособии по математике для 6 класса «Дело о делимости и другие рассказы», составленном названной выше авторской группой [3]. На рис. 3, 4 представлены кадры с фрагментами содержания материала по теме «Дело об определении квадратного уравнения». Эти кадры появляются при нажатии кнопки «теория».
Кроме теоретического материала, представленного в занимательной форме, в ЭУП имеется и справочный материал. В содержании ЭУП он представлен как «Краткий теоретический материал в виде слайдов» (см. рис. 2). Для активизации познавательной деятельности учеников, повышения их интереса к занятиям математикой в ЭУП имеются также познавательные исторические сведения (на рис. 5 представлен кадр с содержанием вкладки «Ученые древности») и занимательные задачи с использованием местного материала (рис. 6). Задачи взяты из учебного пособия профессора С.С. Салаватовой «Мой Башкортостан: математические задачи с краеведческими сюжетами» [6].
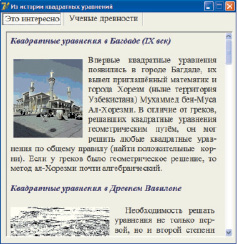
Рис. 5. Вкладка «Это интересно»
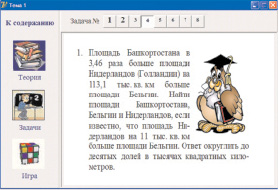
Рис. 6. Задачи с местным материалом
При составлении ЭУП для детей с особыми образовательными потребностями мы исходили из того, что кроме указанных выше достоинств, компьютер может играть немаловажную роль и в нормализации тонуса мышц и моторики артикуляционного аппарата таких детей. Для этого в ЭУП нами включено достаточно много специфических дидактических игр: например, кроссворды, «Домино из уравнений» или же графическое построение различных фигур и др. (рис. 7, 8).
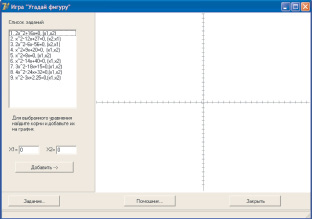
Рис. 7. Интерфейс игры «Угадай фигуру»: начальный этап
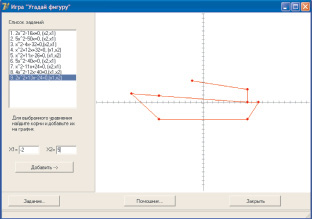
Рис. 8. Интерфейс игры «Угадай фигуру»: конечный этап
На рис. 7, 8 представлены кадры с интерфейсом игры «Угадай фигуру»: начальный и конечный кадры. Опишем кратко ход работы данной программы. При нажатии на кнопку «Задание…» производится загрузка выбранного в диалоговом окне задания. При этом задание из файла загружается в список. В задании пользователю необходимо решить несколько квадратных уравнений, корни которых программой интерпретируются как координаты точек на плоскости прямоугольной декартовой системы координат. На координатной плоскости после решения всех уравнений отобразится определенная фигура, составленная из полученных точек. Значения введенных пользователем корней обрабатываются при нажатии на кнопку «Добавить». При неверном решении уравнения программой предусмотрена возможность повторного решения и исправления ошибок.
Для проверки полученных знаний пользователю ЭУП предоставлена возможность пройти контрольное тестирование по рассматриваемой теме (рис. 9, 10). Контрольное тестирование реализовано в виде внешних исполняемых презентаций MS Power Point, которые загружаются на выполнение непосредственно из ЭУП при нажатии на кнопку.

Рис. 9. Вид входа в контрольный тест

Рис. 10. Фрагмент контрольного теста
Экспериментальное исследование по повышению эффективности обучения детей с особыми образовательными потребностями за счет использования разработанной серии ЭУП проводилось нами на базе МБОУ «СОШ № 15» г. Стерлитамака (с учениками, обучающимися на дому). Причем имелась возможность сравнивать обучение по традиционным учебникам математики, созданным для массовой общеобразовательной школы, и обучение по разработанным ЭУП. Как показал формирующий эксперимент, использование разработанного ЭУП позволило максимально облегчить понимание и запоминание (причем активное, а не пассивное) наиболее существенных понятий, утверждений и примеров, вовлекая в процесс обучения слуховую и эмоциональную память. Повысилось как качество выполняемых домашних заданий учеников, так и их эмоциональное состояние, отношение к урокам математики, к обучению в целом.
Рецензенты:
Михайлов П.Н., д.ф.-м.н., профессор кафедры алгебры, геометрии и методики обучения математике, Стерлитамакский филиал Башкирского государственного университета, г. Стерлитамак;
Дорофеев А.В., д.п.н, профессор кафедры прикладной информатики, технологии и дизайна, Стерлитамакский филиал Московского государственного гуманитарного университета имени М.А. Шолохова,
г. Стерлитамак.
Работа поступила в редакцию 26.10.2012.



