Повышение эффективности управления микробиологическими системами обеспечивает увеличение производительности биореакторов, максимизация которой требует системного анализа закономерностей функционирования протекающих в них процессов с учетом отраслевых особенностей [4]. Трудности проведения такого анализа связаны с недостаточной изученностью микробиологических процессов вследствие их невысокой воспроизводимости и нелинейности. Ограничено также возможностями проведения экспериментальных исследований в промышленных условиях. В связи с отмеченным возрастает роль изучения математических моделей для решения вопроса о принципиальной возможности создания эффективной системы управления. Первоочередной задачей при этом является получение численных значений переменных и констант, являющихся начальными условиями при моделировании динамики объектов и систем управления ими с учетом свойств и особенностей используемых режимов культивирования микроорганизмов.
В соответствии с положениями системного анализа выбор и обоснование оптимальных условий биосинтеза требуют использования критериев эффективности решаемой задачи [1, 2]. Для нахождения оптимальных условий процесса и создания алгоритмов управления, реализующих оптимальные режимы процессов, необходимо представить критерий управления в виде функции цели, экстремум которой наилучшим образом отвечает задачам производства целевого продукта. Эта функция цели должна отражать показатели интенсивности функционирования производства, а также влияние на эти показатели управляющих воздействий. В качестве такой функции цели для микробиологической и медицинской промышленности чаще всего применяют производительность, прибыль от реализации продукта или себестоимость продукта [1]. В первом случае оптимальными считаются условия биосинтеза и управления, максимизирующие выбранный критерий, во втором – минимизирующие его.
Анализируя зависимости технико-экономических показателей опытно-промышленной установки получения биопрепарата от производительности, установлено [1], что прибыль с увеличением выпуска продукции увеличивается, как это показано на рис. 1, и эта тенденция сохраняется до конца исследуемого интервала. Следовательно, увеличение производительности соответствует увеличению прибыли, и критерием оптимального управления процессом (установкой) может быть выбрана максимизация производительности биореактора. Однако следует заметить, что с увеличением производительности затраты, как правило, возрастают непропорционально количеству продукции, в результате чего кривая изменения прибыли при увеличении выпуска целевого продукта имеет максимум в точке F(D) = Fопт (рис. 2). Увеличение выпуска целевого продукта обычно сдерживается предельной мощностью оборудования одной из технологических стадий, образующих узкое место технологического процесса по производительности и не позволяющей увеличить выпуск продукции больше некоторого максимального для данного технологического режима значения Fmax.
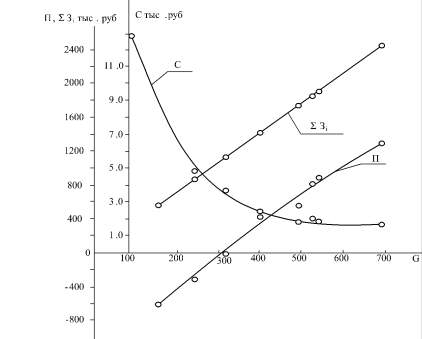
Рис. 1. Зависимость суммарных затрат, себестоимости и прибыли от производительности: ΣЗi – суммарные затраты, тыс. руб.; C – себестоимость, руб.; П – прибыль, тыс. руб.
Следовательно, если во всей области изменения выпуска целевого продукта 0 < F < Fmax, скорость изменения прибыли dП/dF(D) > 0, то задача максимизации прибыли совпадает с задачей получения максимизации производительности. Если же Fmax Fопт, то для обеспечения выбранного критерия необходимо поддерживать величину F = Fопт. При этом нужно учитывать, что вид кривой П = f(F) и значение величины Fопт зависит от характера проведения процесса (периодический или непрерывный) и состояния оборудования.
Таким образом, для управления и моделирования при оптимальных условиях процесса биосинтеза выберем в качестве критерия производительность процесса (количество биомассы, образующейся в единицу времени единицей объема среды в аппарате). Этот критерий в отличие от себестоимости, независимой от времени, дает возможность учитывать при поиске управлений показатели интенсивности функционирования оборудования, т.е. тенденцию к повышению прибыли производства.
Практический интерес представляет определение условий – скорости разбавления D, при которых величина F(D) будет оптимальной. Для моделирования оптимальных по критерию максимальной производительности условий биосинтеза рассмотрим процесс, математическая модель которого представлена системой уравнений [3, 5]:
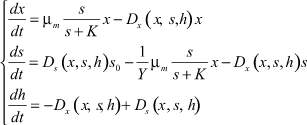 (1)
(1)
где x – концентрация микроорганизмов; μm – максимальная удельная скорость роста; s – концентрация субстрата; K – константа Моно-Михаэлиса или константа полунасыщения, равная концентрации микроорганизмов, при которой скорость их размножения μ(t) = dx/dt равна половине максимальной; Yх/s – экономический коэффициент, равный отношению полученной биомассы к израсходованной массе субстрата Yх/s = ∆x/∆s; Ds(x, s, h), Dx(x, s, h) – потоки через реактор (D = Q/V – скорость разбавления; Q – объемная скорость потока, V – объем реактора).
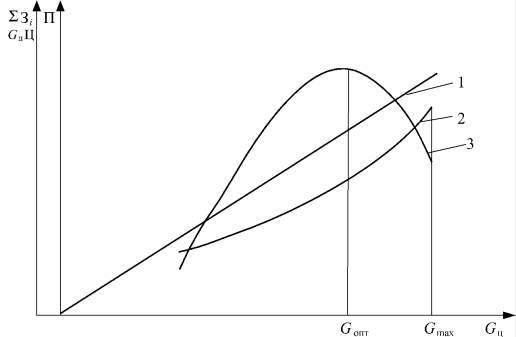
Рис. 2. Изменение прибыли и ее составляющих от производительности: 1 – GцЦ; 2 – суммарные затраты (Зi); 3 – прибыль (П)
Управление таким процессом сводится к регулированию потоков субстрата и продукта, т.е. к определению оптимального характера изменения функций Dx(x, s, h) и Ds(x, s, h). Для этого необходимо установить оптимальный уровень установившегося рабочего потока Ds = Dx = D и оптимальную пороговую концентрацию субстрата, при которой следует начинать его долив. Под оптимальными значениями переменных процесса понимают такие, которые обеспечивают максимум производительности биореакторов по целевому продукту за определенный отрезок времени T. Полагая заданным время процесса биосинтеза Т, целевую функцию управления процессом можно записать в виде максимизации средней производительности за время Т:
![]() (2)
(2)
Процесс можно перевести в квазистационарное состояние в любой момент времени, однако это целесообразно сделать в точке, соответствующей максимуму выражения (2). Для этого рассмотрим работу реактора в стационарном (установившемся) режиме, когда микробная популяция и ее продукты наиболее однородны, концентрации субстрата и продукта становятся постоянными величинами, равно как постоянным становится заполнение аппарата, а их производные стремятся к нулю. Тогда целевая функция упрощается и сводится к следующей
![]()
Следовательно, производительность по целевому продукту (биомассе) как показатель эффективности функционирования биореактора, принимает вид
F(D) = D∙x(D) = Is + (D).
Найдем зависимость производительности по биомассе от скорости разбавления. Для этого приравняем производные в системе дифференциальных уравнений к нулю и из полученной системы алгебраических уравнений выразим эту функ- цию так:
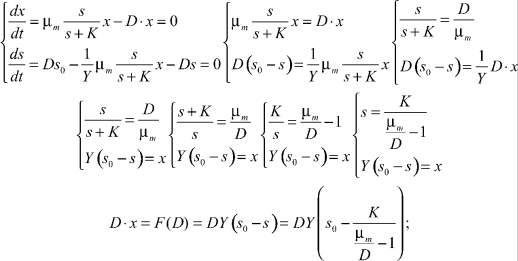
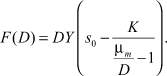 (3)
(3)
На рис. 3 приведена зависимость производительности по биомассе F(D) = D·x(D) от скорости разбавления D при μm = 0,34; s0 = 40; K = 9; Y = 0,8
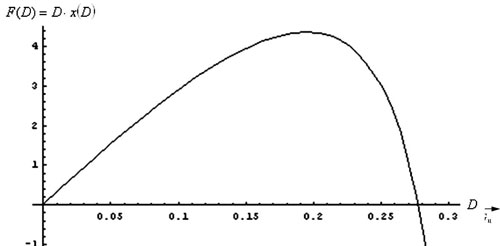
Рис. 3. Зависимость производительности по биомассе от скорости разбавления D
Практический интерес представляет определение скорости разбавления D, при которых величина F(D) будет оптимальной. Для определения экстремума необходимо приравнять нулю частную производную F′(D):
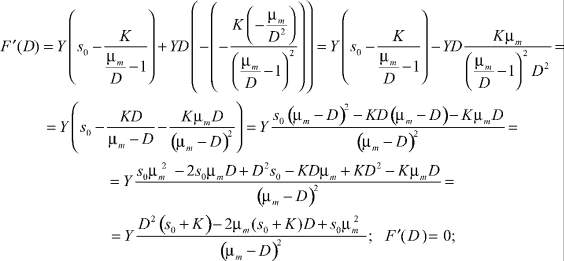
 (4)
(4)
Так как все константы s0, K, μm положительны, производная меняет знак с плюса на минус, т.е. имеет место максимум производительности при Dopt:
![]() (5)
(5)
Как видно, оптимальная скорость вымывания не зависит от экономического коэффициента Y, а зависит только от s0, K, μm.
Определим также равновесную остаточную концентрацию субстрата, равновесную концентрацию продукт при оптимальном потоке. После несложных преобразований получим:
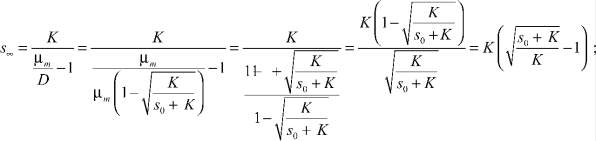
![]() (6)
(6)
![]() (7)
(7)
В нашем случае после подстановки численных значений получаем
![]()
![]()
Как видно из рис. 2 производительность по биомассе в хемостатном процессе сначала возрастает до Dопт, а затем резко падает. Максимум производительности соответствует скорости протока при вымывании , что совпадает с величинами, принятыми на практике. Ограничением по величине скорости протока является значение D = 0,2776 ч –1, т.е. при данной кинетике μ = μ(S, X, D) и данном значении D процесс практически не реализуется. Это связано с тем, что скорость протока настолько велика, что поступающий субстрат полностью вымывается из аппарата и образования продукта и биомассы не происходит.
Другим важным показателем является коэффициент использования Ки [3], который определяется как отношение разности интегрального притока (субстрата) Is+ и интегрального остатка (субстрата) Is– к интегральному притоку:
(8)
где .
Как видно из полученного, Is+ и Ки являются функциями скорости протока среды Ds(t), отбора продукта Dx(t) и концентрации субстрата S(t). Равновесное значение коэффициента использования равно:
(9)
Очевидно, что концентрация x∞ – это и есть та максимальная концентрация дрожжей, которую можно получить. С другой стороны, именно концентрация субстрата s∞ и есть оптимальная пороговая концентрация, при которой следует начинать его доливку.
Полученные численные значения переменных и констант являются начальными условиями для моделирования динамики биообъектов управления. При этом видно, что область вблизи экстремума целевой функции F(D) является нелинейной. Это необходимо учитывать при разработке системы управления процессом биосинтеза, в которой полученные значения переменных процесса являются заданными значениями параметров процесса. Разработка систем управления процессами культивирования микроорганизмов предполагает реализацию полученных данных, исходя из критерия управления, оптимальных условий и комплекса взаимосвязанных задач, которые формируются на основе системного анализа и функционально-алгоритмического синтеза системы.
Рецензенты:Мочалов В.П., д.т.н., профессор, зав. кафедрой «Автоматизированные системы обработки информации и управления» ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Ставрополь;
Лубенцов В.Ф., д.т.н., профессор кафедры «Информационные системы, электропривод и автоматика» Невинномысский технологический институт (филиал) ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Невинномысск.
Работа поступила в редакцию 10.09.2012.



