Бифуркация (тройник) является общим типом разветвления коронарных артерий независимо от их диаметра [8] (рис. 1). В этом типе разветвления каждый сосуд (ствол) разделяется на две ветви. Длина элемента тройника равна расстоянию по стволу от вершины угла предыдущего разветвления, при котором образовался этот ствол, до вершины угла, при котором он распался на ветви (рис. 2). Докапиллярное русло сердца включает в себя генерации сосудов эластического и мышечного типа, а также генерации микрососудов [2, 3]. Диаметр эластических сосудов превышает d = 500 мкм. Сосудами мышечного типа принято считать артерии с диаметром от 100 до 500 мкм. В генерации микрососудов входят артериолы с диаметром менее 100 мкм. Эластические и мышечные сосуды составляют транспортный участок, по которому кислород транспортируется к месту потребления. На микрососудистом, обменном участке происходит диффузия кислорода в окружающие ткани. Транспортные сосуды (100 < d < 500 мкм) разветвляются на две асимметричных ветви. Асимметричность ветвлений этих артерий связана с различным уровнем потребления кислорода различными регионами сердца. Микрососуды (d < 100 мкм) в отличие от транспортных артерий имеют симметричное ветвление [6]; такое ветвление обеспечивает одинаковые условия для диффузии кислорода во всех микрососудах и капиллярах [5].
Бифуркация – оптимальный вариант ветвления докапиллярных сосудов
В любом сосуде затраты энергии разделяются на две составляющих:
1) расход энергии на перемещение крови;
2) расход энергии на химические процессы в крови.
Механическая и «химическая» составляющие с изменением диаметра сосуда изменяются в противоположных направлениях. В случае возрастания диаметра сосуда (при неизменной длине) расход механической энергии увеличивается, а химической, напротив, уменьшается. Минимальный суммарный расход при заданном кровотоке имеет место, если есть соотношение [4]
![]() (1)
(1)
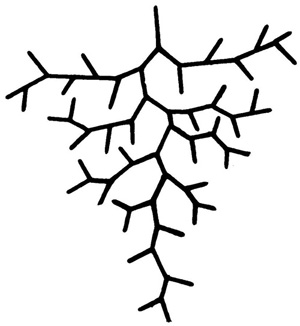
Рис. 1. Артериальное дерево
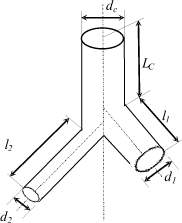
Рис. 2. Сосудистый тройник. dС, d1, d2, lС, l1, l2 – соответственно диаметр и длина ствола, 1 и 2 ветвей
Естественно, что при бифуркационном ветвлении:
![]() (2)
(2)
где dC, d1, d2 – диаметр ствола, 1 и 2 ветвей.
Соотношение (1) сохраняется и для других вариантов ветвления. В частности, энергооптимальная трифуркация может быть представлена следующим отношением между стволом и ветвями:
![]() (3)
(3)
где dС, d1, d2, d3 –соответственно диаметры ствола, 1, 2 и 3 ветвей.
Представим доказательства того, что энергооптимальный вариант бифуркации является наиболее выгодным вариантом ветвления сердечных сосудов по сравнению с энергооптимальной трифуркацией, энергооптимальной тетрафуркацией и т.д. По сравнению с другими возможными вариантами ветвления (3, 4, 5 и более ветвей) бифуркация, как будет показано ниже, обеспечивает значительные преимущества. Для сравнения рассмотрены наиболее близкие варианты: бифуркация (ствол и 2 ветви) и трифуркация (ствол и 3 ветви). Предварительно для обоих вариантов примем условия равенства следующих параметров:
1) одинаковая разность давлений между аортой и артериальным концом капилляров;
2) равенство кровотока в первой коронарной артерии;
3) одинаковый диаметр первой коронарной артерии и одинаковый диаметр капилляров;
4) одинаковая плотность капиллярной сети;
5) во всех сосудах бифуркационных и трифуркационных разветвлений имеет место режим «минимальной работы»;
6) суммарные величины расхода энергии, объема крови и проводимости на докапиллярном участке одинаковы для обоих вариантов.
Для упрощения расчетов примем симметричными все бифуркационные (d1 = d2) и трифуркационные (d1 = d2 = d3) разветвления. Примем также, что вязкость крови, отношение длины сосуда l к диаметру d одинаковы для всех докапиллярных сосудов в обоих вариантах:
C = l/d = const. (4)
Исходя из (2) и (4), при каждой бифуркации
![]() (5)
(5)
где lС, l1, l2 – длина ствола и 1 и 2 ветвей. Соответственно, с учетом выражений (3) и (4) для каждого трифуркационного разветвления имеем:
![]() (6)
(6)
где lC, l1, l2, l3 – длина ствола и 1, 2 и 3 ветвей при трифуркационном ветвлении.
В соответствии с (2), (4) и (5) при симметричном бифуркационном ветвлении имеем:
d1 = d2 = 0,794dС, (7)
l1 = l2 = 0,794lС. (8)
Для трифуркации, исходя из (3), (4) и (6),
d1 = d2 = d3 = 0,694dС, (9)
l1 = l2 = l3 = 0,694lС. (10)
Количество докапиллярных бифуркационных ветвлений Nбиф определяется по формуле [5]:
Nбиф = (ln dA – ln dk)/ln 1,26, (11)
где dA, dk – соответственно диаметр первой коронарной артерии и капилляра.
Количество трифуркационных ветвлений Nтриф определяется по формуле:
Nтриф = [ln dA – ln dk]/ln 1,44. (12)
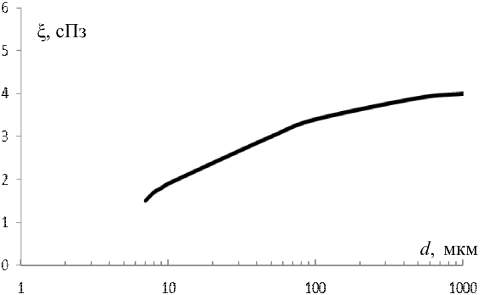
В проведенных нами ранее расчетах для собаки [5], исходя из предварительного условия (1), а также отношений (7), (9), (11) и (12) при бифуркации и трифуркации общее число докапиллярных генераций равно соответственно 28 и 18. Для соблюдения условий (1) и (6) длина всех «трифуркационных» сосудов и давление на каждом из них по сравнению с «бифуркационными» должны возрасти в 1,6 раза, что соответствует аналогичному увеличению объема и сопротивления каждого сосуда. При таком увеличении общий расход энергии, сосудистого материала и крови на всем докапиллярном русле для обоих вариантов ветвления будет одинаковым. Для простоты расчетов кровь временно рассматривается как ньютоновская жидкость, вязкость которой не зависит от диаметра. С учетом этого кривая вязкости на рис. 3 представляла бы прямую, параллельную оси диаметров (см. рис. 3). Исходя из (7) и (9), очевидно, что количество обменных сосудов в каждой одноименной m-генерации (m = 1, 2, 3 т.д., начиная от капилляров) при бифуркации будет больше, чем при трифуркации. При «ньютоновской» крови в пределах обменного участка (7 £ d £ 45 мкм), на котором происходит диффузия кислорода (см. таблицу, столбцы 1, 2 и 5), суммарная боковая поверхность всех «бифуркационных» и «трифуркационных» сосудов равняется соответственно Sбиф = 2480S1 и Sтриф = 1590S1 (S1 – боковая поверхность первой коронарной артерии) [5]. С учетом спадающего участка кривой вязкости крови в тех же пределах (7 £ d £ 45 мкм), где кровь реально проявляет себя как неньютоновская жидкость (рис. 3), и величин, представленных в таблице (столбцы 1, 2, 3), имеем: Sбиф = 3990S1 и Sтриф = 2320S1 [5]. Таким образом, имеет место «прирост» дополнительной «бифуркационной» боковой поверхности на «обменном», спадающем участке кривой x = f(d) за счет неньютоновских свойств крови. Это приращение в 2 раза больше, чем в трифуркационном варианте (DSбиф/DSтриф = 2,07). Очевидно, что при дальнейшем росте разветвлений ствола «дополнительный» прирост боковой поверхности на обменном участке будет уменьшаться в еще большей степени.
Гемодинамические и кислородные параметры обменных артериол сердца при бифуркационном ветвлении [5]
|
m |
dm |
Сm |
tm |
Um |
DHbO2m |
DpO2m |
|
1 |
6,9 |
6 |
37,0 |
138,3 |
5,04 |
11,0 |
|
2 |
8,7 |
6 |
37,0 |
87,0 |
3,10 |
10,5 |
|
3 |
11,0 |
5 |
30,9 |
54,7 |
1,66 |
6,9 |
|
4 |
13,9 |
5 |
30,9 |
34,4 |
1,05 |
4,9 |
|
5 |
17,5 |
4 |
24,6 |
21,6 |
0,52 |
3,6 |
|
6 |
22 |
4 |
24,6 |
13,6 |
0,30 |
3,5 |
|
7 |
27,8 |
4 |
24,6 |
8,5 |
0,14 |
2,4 |
|
8 |
35,0 |
3 |
18,5 |
5,3 |
0,08 |
1,1 |
|
9 |
44,0 |
3 |
18,5 |
- |
- |
- |
Примечания. m – номер обменного сосуда цепочки по направлению капилляр – аорта; dm – диаметр сосуда, мкм; Cm – отношение длины к диаметру; tm – время пребывания эритроцита в m-сосуде, мкс; Um – скорость отдачи кислорода отдельным эритроцитом в поперечном сечении m-сосуда, %/с; DHbO2m – количество кислорода, отданного отдельным эритроцитом за время пребывания в m-сосуде, %; DрО2m – разность напряжений кислорода на концах m-сосуда, мм рт. ст.
Рассмотрим дополнительные преимущества бифуркаций на обменном участке. Эритроцит отдает кислород при прохождении сосудов диаметром не более 45 мкм (см. таблицу, столбцы 1, 2, 6). В остальных сосудах отдача кислорода незначительна и ею при расчетах можно пренебречь. По мере увеличения числа ветвлений (3, 4, 5 и т.д.) количество генераций, «совпадающих» с наклонным сегментом кривой до d £ 50 мкм, стремительно уменьшается. На обменный участок в пределах d = 7–50 мкм приходится 9 бифуркационных разветвлений, а трифуркационных только шесть [5]. При дальнейшем росте ветвлений (4, 5 и т.д.), количество «совпадений» с наклонным участком кривой будет уменьшаться в еще большей степени. Очевидны «кислородные» преимущества бифуркационного разветвления перед всеми остальными. Если рассматривать обменные генерации, начиная от капилляра, то в «одноименных» генерациях диаметр «небифуркационных» сосудов возрастает быстрее, чем «бифуркационных». Например, для первой от капилляров генерации при бифуркации d1 = 1,26dk, при трифуркации d1 = 1,44dk, при тетрафуркации d1 = 1,59dk и т.д. Показано [5], скорость отдачи кислорода отдельным эритроцитом в поперечном сечении сосуда тем меньше, чем больше диаметр последнего (таблица, столбец 5). Следовательно, отдельный эритроцит в поперечном сечении трифуркационного сосуда отдает за единицу времени кислорода меньше, чем в «одноименном» бифуркационном. Кроме того, общее время пребывания эритроцитов в «трифуркационных» сосудах меньше, чем в «бифукационных».При бифуркации отдельный эритроцит на цепочке обменных микрососудов до капилляра отдает 12 % кислорода, а при трифуркации только 8,3 % [5]. Очевидно, что эритроцит при прохождении «трифуркационной» цепочки обменных сосудов не успевает «разрядиться» до нормального «бифуркационного» напряжения рО2кап = 50 мм рт. ст. на входном конце капилляра. При трифуркации уменьшается «резерв» рО2, используемый при внешних возмущениях (например, при физической нагрузке). Вследствие этого максимальный уровень допустимой нагрузки, при котором сердечная мышца еще получает адекватное кислородное обеспечение, снижается. При превышении этого уровня сердечные клетки начинают испытывать кислородное голодание и погибают. Очевидно, что при дальнейшем росте ветвлений (n = 4, 5 и т.д.) уровень допустимой физической нагрузки будет снижаться в возрастающей степени. Таким образом, при бифуркации допустимый верхний уровень физической нагрузки имеет наибольшую величину. Отметим, что теоретически возможен еще один вариант ветвления – сквозной, при котором ветвления отсутствуют, а все сосуды (включая и капилляры) имеют одинаковый диаметр. Очевидно, что при таком варианте обеспечение миокарда кислородом было бы крайне неэкономичным.
Ранее было показано [5], что каждый обменный микрососуд, отдающий кислород, является «кислородным» эквивалентом сердечного капилляра той же длины. При соблюдении предварительных условий (1)–(6) наклонному участку кривой вязкости бифуркация обеспечивает наибольшую плотность докапиллярных микрососудов (7 < d < 100 мкм), отдающих кислород. Таким образом, очевиден выигрыш бифуркационного ветвления: большая, чем при трифуркации, плотность и протяженность «обменной» сети при одинаковом расходе энергии, крови и сосудистого материала.
С бифуркацией связано еще одно преимущество. При бифуркации всякой генерации обменных сосудов, начиная от капилляров, по сравнению с «одноименными» генерациями других вариантов ветвлений соответствует наименьшая величина диаметра. Следовательно, величина отношения поверхности S к объему сосуда V (S/V = 4/d), обусловливающая уровень метаболизма между кровью и тканью, в «одноименных» генерациях при бифуркации всегда будет большей, чем в любом другом варианте ветвления. В «одноименных» бифуркационных генерациях метаболизм достигает максимальных значений. Таким образом, из всех возможных вариантов ветвления (n = 1, 2, 3, 4…) Природа «выбрала» бифуркацию (n = 2) как наиболее эффективный вариант, который обеспечивает не только максимальную обменную поверхность, но и наиболее эффективное «использование» последней.
Очевидна исключительная важность в оптимизации коронарного русла за счет «подбора» размеров сосудов. Если «подбором» диаметра обусловливается общее количество ветвлений и энергооптимальный характер движения кровотока в каждом «бифуркационном» сосуде, то «подбор» длины сосудов обеспечивает в конечном счете приблизительное равенство давлений на входе всех микрососудов (d » 100 мкм). За счет изменения длины обеспечивается одинаковое по времени продвижение отдельных эритроцитов из одного и того же микрообъема крови на входе первого сосуда до входа в «свой» микрососуд. Это условие должно выполняться из условия принципа постоянства суммарного кровотока по всем сосудам в любой момент времени. Таким образом, на вход обменного участка каждый из этих эритроцитов должен приходить за одинаковое время и с одинаковым давлением. Отмеченными факторами обеспечиваются одинаковые условия оптимального движения крови и оптимальной диффузии кислорода в обменных микрососудах и капиллярах, поскольку в микрососудах имеет место симметричное ветвление сосудов (d1 = d2, l1 = l2) [6]. Тем самым обеспечивается одинаковое «качество» кислорода, поступающее в ткани из «одноименных» сосудов (см. таблицу, столбцы 5–7). Необходимо отметить при этом полную аналогию микрососудистого русла у различных видов млекопитающих [1].Заключение
В заключение можно сказать, что бифуркация и оптимальный «подбор» диаметров и длин сосудов на докапиллярном участке обеспечивают условия для наиболее эффективного метаболизма между кровью и сердечными клетками и энергооптимального обеспечения сердечной мышцы кислородом, чем при любом другом варианте ветвления. Выявленные особенности бифуркационного ветвления коронарных сосудов представляют значительный интерес для понимания оптимальности организации докапиллярного русла. Представленная организация гемодинамики и архитектоники бифуркаций позволяет приблизиться к более полному пониманию основ крово-кислородного обеспечения сердца человека и млекопитающих.
Рецензенты:Каминский Ю.Г., д.б.н., зав. лабораторией метаболического моделирования и биоинформации Института теоретической и экспериментальной биофизики РАН, г. Пущино;
Чемерис Н.К., д.б.н., профессор, главный научный сотрудник лаборатории биомедицинских проблем Института биофизики клетки РАН, г. Пущино.
Работа поступила в редакцию 11.07.2012



