1. Введение
При движении КА в атмосфере точный учет внешних возмущающих сил затруднителен, так как они либо неизвестны, либо имеют сложный характер. К таким внешним воздействиям можно отнести вариации плотности атмосферы, ветер, турбулентное движение воздуха, погрешности отработки управляющих воздействий и измерений и т. д. Указанные обстоятельства приводят к рассмотрению задачи движения КА в условиях неопределенности.
В работе исследуется проблема использования непрерывных марковских процессов для получения статистических характеристик параметров движения спускаемого аппарата без проведения массовых расчетов возмущенных траекторий, что позволит существенно сократить машинное время для получения количественных оценок точности посадки КА.
2. Стохастическое описание движения КА в атмосфере
Рассмотрим детерминированное представление движения КА в атмосфере в скоростной системе координат:
![]()
![]() ={V, Θ, ε, h,λ, φ} (1)
={V, Θ, ε, h,λ, φ} (1)
Здесь обозначения аналогичны приведенным в [1]. Будем считать, что движение КА, описываемое системой дифференциальных уравнений, представлено в виде нестационарных пуассоновских потоков событий, состоящих в последовательных переходах аппарата из одного состояния в другое [2]. Это позволяет использовать математический аппарат теории марковских процессов.
Будем полагать, что КА может находиться в конечном числе состояний, которое определяется заранее выбранным алгоритмом дискретизации фазового пространства. Каждое состояние характеризуется шестимерным вектором ik(k=1,6) фазовых координат. Нахождение КА в каждом состоянии определяется вероятностью Р(ik). Причем ![]() При известных значениях Р(ik) математическое ожидание фазовых координат КА может быть рассчитано по формуле
При известных значениях Р(ik) математическое ожидание фазовых координат КА может быть рассчитано по формуле
![]() (2)
(2)
где Jk - количество состояний на всей k-й оси шестимерного фазового пространства.
При изменении вероятностей Р(ik), очевидно, изменяется и вектор математических ожиданий М[xk]; тем самым моделируется движение КА.
Согласно закону распределения Пуассона вероятность одного случайного события (в нашем случае вероятность одного перехода в заданное состояние в единицу времени) определяется формулой Р(t)=λ(t)е-λ(t),
Интенсивности пуассоновских потоков будем принимать равными нормированным значениям правых частей дифференциальных уравнений (1) в фиксированных фазовых состояниях:
![]()
где Δxk - интервал разбиения по k-й оси.
Для определения вероятности нахождения КА в каждом из заданных состояний составим систему дифференциальных уравнений Колмогорова. Общее уравнение для произвольного состояния с координатами ik имеет вид
![]() (3)
(3)
В результате получим систему обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами размерности ![]()
Таким образом, пространственное движение КА в атмосфере, описываемое дифференциальными уравнениями (1), может быть также представлено в стохастическом варианте, т. е. в виде системы из N линейных дифференциальных уравнений для вероятностей переходов (3) и аналитических зависимостей (2) для вычисления вектора математических ожиданий фазовых координат.
3. Метод учета случайных возмущающих факторов
Будем использовать стохастический вариант, основное преимущество которого перед детерминированным состоит в принципиальной возможности учета в правых частях дифференциальных уравнений слагаемых, характеризующих случайные воздействия.
Общий вид исходной системы дифференциальных уравнений КА следующий:
х=f(х, и, t)+G(х,t)ξ(t), (4)
где х, u-векторы фазовых переменных и управления, G(х,t) - матрица размером k´k (в рассматриваемом случае k=6).
Для представления процессов, описываемых системой (4) с помощью марковской цепи, воспользуемся ФПК- уравнением [2]
![]()
Здесь ρ - плотность вероятности. Коэффициенты а(х, и, t) и b(х, t) являются числовыми (не случайными) функциями. Физически а(х, и, t), b(х, t) характеризуют скорость изменения функции х(t) и условной дисперсии случайной функции f(t) соответственно. Коэффициенты аi(х, и, t) и bjk(x,t) определяются из уравнений
aj (х, u, t) = fj (х, u, t), ![]()
Проведем дискретизацию фазового пространства подобно тому, как это делалось для варианта без возмущений. Общее уравнение Колмогорова для произвольного состояния с, ik (k=1,6) запишется следующим образом:
![]() (5)
(5)
при ij=1λj(ik,k≠j,ij-1)=0.
Величины μj можно интерпретировать как мгновенные значения интенсивностей потоков, переводящих КА в соседние состояния в результате воздействия случайной функции. В общем случае величина μj , вычисляется по формуле
![]()
Итак, интегрируя систему N дифференциальных уравнений типа (5) и используя полученные значения вероятностей Р(ik) для вычисления математических ожиданий (2), можно определить траекторию движения КА в атмосфере с учетом влияния случайных возмущающих воздействий с известными статистическими характеристиками.
Для сокращения продолжительности вычислительного процесса рассматриваются не все состояния фазового пространства, полученные в результате его дискретизации, а лишь те, вероятность нахождения аппарата в которых превышает заданную величину Р*, а также соседние с ними состояния. Когда для какого-либо крайнего состояния Sijk вероятность Р(i,j,k) достигает величины Р*, прибавляются новые состояния, в которые КА может непосредственно перейти из Sijk, а вероятности нахождения аппарата в новых состояниях в этот момент принимаются равными нулю. И наоборот, те состояния, для которых вероятность становится меньше Р*, перестают рассматриваться.
Во избежание чрезмерного увеличения размерности интегрируемой системы уравнений в определенный момент времени t* за новые начальные значения фазовых координат принимаются значения математических ожиданий рассчитанные по формуле (2).
4. Заключение
Проведенный сравнительный анализ результатов, полученных с помощью предлагаемого метода и с применением известных методов численного интегрирования системы дифференциальных уравнений (1) показал, что погрешности вычислений, полученных с использованием предлагаемого метода не превышают 5% (например, табл. 1, рис.1.)
Таблица 1. Погрешности расчетов траекторных параметров движения КА в атмосфере (номинальный вариант: V0 =7,5 км/с, Θо=-3°, Кб =0,5, Рx=1,5×104 кг/м2, ε0=3°, hk=20 км)
|
Варьируемые параметры |
Vk , км/с |
δVk , % |
|
|
1 |
2 |
||
|
Номинальный вариант |
2,34 |
2,39 |
2,14 |
|
V0=7,8 км/с |
2,64 |
2,72 |
3,03 |
|
V0=7,3 км/с |
2,73 |
2,77 |
1,47 |
|
Кб =0 |
5,82 |
5,91 |
1,55 |
|
Кб =1 |
2,00 |
2,07 |
3,50 |
|
Рx =104 кг/м2 |
2,14 |
2,19 |
2,34 |
|
Рх=2×104 кг/м2 |
2,84 |
2,88 |
1,41 |
|
Θо=-4° |
3,34 |
3,39 |
1,50 |
|
Θо =-5° |
2,48 |
2,51 |
1,21 |
|
ε0=4° |
2,34 |
2,39 |
2,14 |
|
ε0=5° |
2,34 |
2,39 |
2,14 |
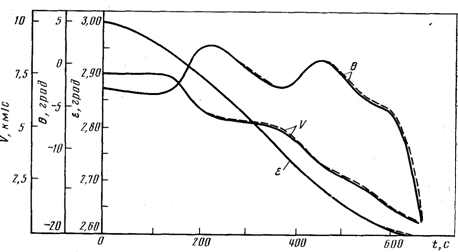
Рис. 1. Зависимости скорости V, траекторного Θ и курсового eе углов от времени t (Vo=7,5 км/с, Θ0=-30, ε0=3°, Кб =0,5, Рх==1,5-104 кг/м2). Сплошные линии-численное интегрирование уравнений (1). Штриховые линии - аналитический метод.
Таким образом, проведенные исследования показали принципиальную возможность использования предложенного для анализа возмущенных траекторий движения КА в атмосфере. Окончательное заключение об эффективности метода по сравнению с известными может быть сделано после его апробирования при решении задач с учетом определения статистических характеристик случайного процесса посредством обработки реальной измерительной информации.
СПИСОК ЛИТЕРАТУРЫ:
- Соколов Н. Л. Приближенный аналитический метод расчета пространственных маневров космического аппарата в атмосфере//Космич. исслед 1988 Т. 26 Вып. 2. С. 209.
- Пугачев В. С., Казаков И. Е., Евланов Л. Г. Основы статистической теории автоматических систем. М.: Машиностроение, 1974.



