То, что сила аэродинамического сопротивления, действующая на вращающееся тело, существенно отличается от той же силы, действие которой испытывает тело при прямолинейном движении, не вызывает сомнений. Во-первых, в первом случае речь идет о динамическом режиме [1], в котором может проявлять себя, к примеру, эффект присоединенной массы [2]. Во-вторых, скорость протяженного тела при вращательном движении становится неопределенной величиной. Наконец, при вращательном движении наиболее заметной может быть интерференция обтекания тела воздухом [3]. Известные же экспериментальные результаты [4,5] в основном относятся к прямолинейному движению тела в воздухе. Более того, будучи полученными из экспериментов в аэродинамических трубах, если строго, они описывают не силу, испытываемую движущимся в воздухе телом, а силу, с которой движущийся воздух действует на покоящееся тело. Даже если такие опасения преждевременны, все это должно быть проверено, разумеется, экспериментально.
Элемент поверхности hdr плоскости, вращающейся с угловой скоростью w, испытывает действие силы аэродинамического сопротивления
![]() , (1)
, (1)
где ρ - плотность воздуха, С - коэффициент аэродинамического сопротивления. Отсюда следует, что момент силы аэродинамического сопротивления, действующего на вращающуюся плоскость, должен быть равен
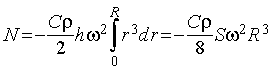 , (2)
, (2)
а уравнение движения подвижной части измерительной установки после выключения двигателя (рис. 1) приобретает вид
![]() , (3)
, (3)
где S - площадь плоскости, J - момент инерции подвижной части измерительной установки, включающей, в том числе, и ротор двигателя. Второе слагаемое в правой части уравнения (3) описывает момент сил сопротивления, испытываемого подвижной частью установки без плоскости. Сюда входит также момент сил, обусловленный трением в осях двигателя. Решение уравнения для системы, нагруженной исследуемой плоскостью:
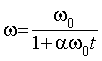 , (4)
, (4)
где w0 - угловая скорость вращения плоскости в момент времени t=0 и
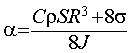 (5)
(5)
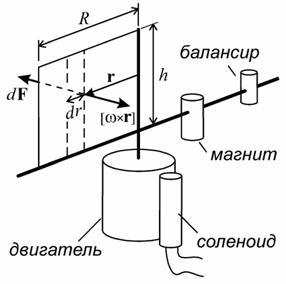
Рис. 1. Схема эксперимента
- для системы нагруженной исследуемым телом и
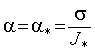 (6)
(6)
- для подвижной системы без плоскости. Отсюда
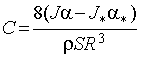 . (7)
. (7)
Моменты инерции ненагруженной и нагруженной подвижной части определяются либо расчетным путем, либо экспериментально. В последнем случае следует провести дополнительное измерение для системы, момент инерции которой увеличен на известную величину. Коэффициенты a и a* определяются исходя из следующих соображений. Поскольку угловая скорость вращения ω связана с углом поворота φ выражением ω=dφ/dt, то
![]() , (8)
, (8)
где ω0 - угловая скорость подвижной части в момент времени t=0. Пусть ti -моменты времени, в которых индукционный ток максимален (рис. 2), что в той или иной степени соответствует минимальному расстоянию между вращающимся источником магнитного поля (постоянным магнитом), установленном на одном плече подвижной части системы, и соленоидом. Тогда моменты времени ti+1 и ti должны удовлетворять необходимому условию
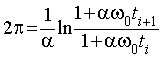 .
.
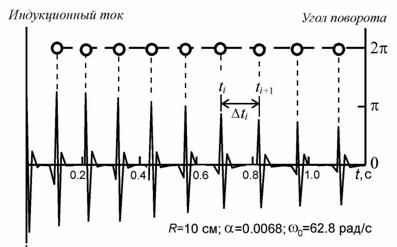
Рис. 2. Индукционный ток как функция времени
Более того, неизвестные величины a и w0 являются нетривиальным (ненулевым) решением системы уравнений
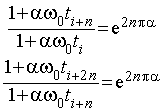 . (9)
. (9)
При этом система уравнений (9) имеет аналитическое решение, что, по существу, делает задачу корректно поставленной. Другими словами, это позволяет не только определить коэффициент аэродинамического сопротивления, но и выяснить его зависимость от скорости. Однако, самый важный и самый интересный результат заключается не в этом. Во-первых, определенный таким образом коэффициент аэродинамического сопротивления оказался более чем в два раза больше известного значения для плоскости 1.1 [4,5]. Совершенно неожиданной оказалась нерегулярность коэффициента C при изменении горизонтального размера вращающейся плоскости (рис. 3). Наиболее подозрительным кажется существование минимума коэффициента аэродинамического сопротивления в зависимости от R при частоте вращения около 10 Гц. Ясно, что это не является результатом методической ошибки. Об этом свидетельствуют результаты, соответствующие сравнительно низким начальным угловым скоростям вращения w0. С другой стороны, маловероятно, что это последствие так называемого кризиса аэродинамического сопротивления [6]. Резкое уменьшение коэффициента аэродинамического сопротивления, называемое кризисом, должно наступать при числах Рейнольдса Re, составляющих величину около 3×105. Минимум же величины С, показанный на рис. 3, имеет место при Re≈ρω0R2/2μ=2.2×104. А вообще, считается, что кризис аэродинамического сопротивления для плоскости должен отсутствовать [6]. С другой стороны, продемонстрированные выше результаты относятся к скоростям, где аэродинамическое сопротивление является квадратичным по скорости, а его коэффициент должен иметь постоянное значение, приблизительно равное 1.1. Едва ли этот вывод нуждается в проверке. Детальному изучению должны быть подвергнуты особенности аэродинамического сопротивления, возникающие в динамическом режиме. Кстати говоря, косвенным подтверждением приведенных выше результатов является попытка измерить силу аэродинамического сопротивления, действующего на маятник Максвелла, снабженный лопастями [7]. Не отличаясь достаточной точностью, такие измерения, как оказалось, тем не менее предлагают коэффициент аэродинамического сопротивления C≈2.6.
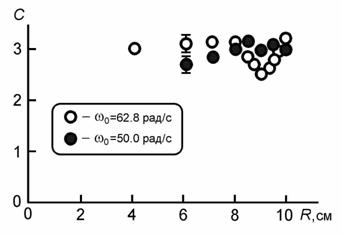
Рис. 3. Коэффициенты аэродинамического сопротивления при различных размерах плоскости и начальных угловых скоростях вращения
СПИСОК ЛИТЕРАТУРЫ:
- Герасимов С.А. Об автомодельности аэродинамического сопротивления. // Вестник машиностроения. 2007. № 1. С. 34-35.
- Седов Л.И. Механика сплошной среды. Т. 2. - М.: «Лань», 2004. - 560 с.
- Петров К.П. Аэродинамика тел простейших форм. - М.: «Факториал», 1998. - 432 с.
- Sovran G., Morel T., Mason W.T. Aerodynamic Drag Mechanisms of Bluff Bodies and Road Vehicles. - New York: Plenum Press, 1978. - 360 p.
- Pivit R. Measuring Aerodynamic Drag. // Radfahren. 1990. V. 2. P. 44-49.
- Ландау Л.Д., Лифшиц Е.М. Гидродинамика. - М.: Физматлит, 2006. 736 с.
- Благодарный В.В. Маятник Максвелла в опытах по аэродинамике. // Учебная физика. 2007. № 1. С. 103-106.



