Для объяснения эффекта допускаем, что свет, идущий от источника света, связан с источником и распространяется от него со скоростью с = 3 · 108 м/с относительно источника. Для приемника скорость света относительно источника будет складываться со скоростью источника v.
Чтобы определить зависимость частоты света ν от скорости v, рассмотрим распространение света от двух источников, один из которых Ѕ движется по направлению от приемника со скоростью v, а другой S0 покоится.
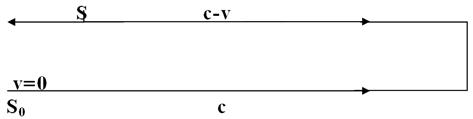
Рис. 1.
Одинаковые источники излучают свет одинаковой частоты ν0. Свет относительно источников распространяется с одинаковой скоростью с, поэтому и длина излучаемой волны λ0 будет одинакова. К приемнику от движущегося источника свет подойдет со скоростью с-v и длина волны λ0 будет принята за время Т = 
(период), а от покоящегося источника - за время Т0= 
. Периоды есть величины обратные частотам колебаний 
и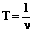 
. Подставим значения Т и Т0 в полученные равенства
и 
,
разделив их почленно, получаем
,
получаем [1] [с. 18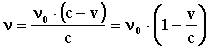1].
(1)
В случае, когда источник и приемник сближаются, надо знак v заменить на противоположный, получим 
. Отметим, что с-v и c - это скорости света соответственно относительно приемника и источника света.
Теперь рассмотрим случай, когда источник света движется перпендикулярно направлению на приемник. Учитывая, что свет связан с источником, распространяется относительно его со скоростью с и сносится с ним со скоростью v, чтобы он попал на приемник его надо направить под некоторым углом α так, что sinα = 
. В этом случае составляющая скорости света, совпадающая с направлением на приемник А будет 
, составляющая v на это направление равна 0. Чтобы не повторять предыдущие рассуждения, воспользуемся формулой (1), с-v заменим на , а скорость с относительно источника останется неизменной. В результате получаем:
,
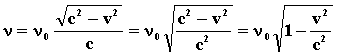что соответствует результату, полученному в опытах Айвса [1] [с. 181].
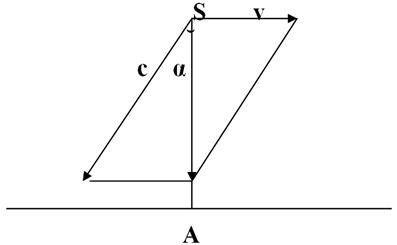
Рис. 2.
При переходе света от источника к приемнику меняется его частота от ν0 до ν. Из формулы с=λν следует, что должна меняться и длина волны. Если от источника света шла волна длиной λ0, то приемник получит ее другой, допустим λ. Получить значение λ можно, воспользовавшись тем, что λ и ν величины обратно пропорциональные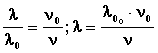 
. Подставив значение ν из формулы (1), получим
. (2)
Для большей уверенности получим эту формулу другим способом.
Любой приемник света может быть и излучателем, значит, он имеет такую же светонесущую среду, как и источник, и свет в ней распространяется со скоростью с. Свет, переходя из среды источника в среду приемника, получает скорость с относительно приемника.
Волна длиной λ0 от источника к границе раздела сред источника и приемника подходит со скоростью с - v и границу пройдет за время 
C самого начала входа волны в сферу среды приемника ее начало приобретает скорость с относительно приеника и за время Т пройдет путь λ = сТ. Подставив значение Т, получаем:
(2)
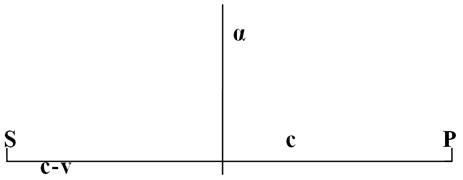
Рис. 3.
В первой половине ХХ в. американский ученый Хаббл в спектрах далеких звезд обнаружил смещение спектральных линий в сторону красной части спектра по сравнению с лабораторными спектрами - «красное смещение». Это означало, что длина принимаемой волны λ больше, чем λ0 и чем дальше звезда, тем больше «красное смещение».
В формулу (2) входят четыре величины λ, λ0, с и v. Кo времени открытия «красного смещения» скорость света с постулатом Эйнштейна была закреплена постоянной относительно любой системы отсчета, значит, и λ0, связанная со скоростью света с и источником излучения, оказалась постоянной. В формуле (2) переменная величина λ, оказалась связанной со скоростью источника v. Увеличение λ вызывает и увеличение v.
«Красное смещение» наблюдается у звезд, расположенным по всем направлениям, поэтому был признан факт расширения Вселенной.
В астрономии связь между λ и v определяется другой формулой [2] [47]
(3)
для удаляющегося источника излучения.
Для одного и того же явления и одних и тех же величин двумя формулами устанавливается разная зависимость! Чтобы разобраться с этим, сравним результаты, которые дают эти формулы при различных v. Ограничений на значение скорости v формулы не требуют. Для удобства длины волн обозначим λ3 и λ2 соответственно обозначению формул (3) и (2), в которые они входят. При v=0:
.
При 0< v< с сравним делением:
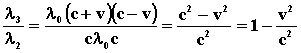
Если v«с, то 
и λ3 ≈ λ2. При этих двух условиях результаты практически не противоречат друг другу.
При v = с; 
λ2 превращается в бесконечность, при этом формула (1) дает 
. Получается, что световая волна от источника к приемнику не попадает, она со скоростью с от источника будет двигаться к приемнику и вместе с источником будет с такой же скоростью уходить от него с - с = 0.
Третье сравнение требует сделать вывод, какая же формула правильно отражает действительность. Происхождение формулы (2) рассмотрено в начале статьи. Теперь рассмотрим, как получается формула (3).
Рис. 4.
Представим, что источник света окружен средой, в которой свет распространяется к приемнику со скоростью с. Источник света в точке А начал излучать волну. Время излучения одной волны обозначим Т (период). С момента появления начала волны оно начинает перемещаться к приемнику в окружающей среде со скоростью с и за время Т удалится от точки А на расстояние сТ. Но за это же время источник, двигаясь от приемника окажется в точке С, пройдя расстояние АС = vТ, где и окажется конец волны. Расстояние от С до В и будет длиной волны λ = сТ +vТ = (с + v)Т
Если источник не движется, то v = 0 и длина волны будет λ0 = сТ. Разделив λ на λ0, получим:
(3).
В начале статьи мы рассмотрели среду, которая обеспечивает скорость света с, она либо связана с источником, либо с приемником света. Первая - дает формулы (1) и (2). Вероятность того, что вторая, от далеко расположенного приемника света, на скорость света больше влияла, чем среда источника света, ничтожно мала. Остается среда, не связанная ни с источником ни с приемником света, которая действует подобно воздуху (веществу) на распространение звука. Но отрицательный результат опытов Майкельсона по обнаружению «эфирного ветра» доказал, что такой среды в природе нет. Остается сделать предпочтение формуле (2). Ранее отмечалось, что при удалении источника света со скоростью v = с волна не достигнет приемника, и сигнал не будет получен.
Хабл ввел закон, носящий его имя [2] [с. 120]
v = НD,
где v - скорость удаления источника света, D - расстояние между источником и приемником, Н - коэффициент пропорциональности, называемой постоянной Хабла.
.
1 Мпк = 106 пк; 1пк (парсек) = 3,26 светового года = 3.1013 км.
Найдем расстояние, при котором v = с: 
;
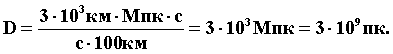
D - это радиус сферы, ограничивающей прием прямого электромагнитного излучения из просторов Вселенной. Из прилегающих к этой сфере зон во внутренней ее части электромагнитные излучения могут приходить только в виде радиоволн. В природе не наблюдается какого-либо приоритетного направления в распределения звезд, поэтому радиоизлучение должно приходить со всех сторон равномерно.
Рассмотрим вариант, когда v>с. В этом случае формулы (1) и (2) дают: 
и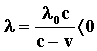 
.
Это означает, что волна должна приходить с направления, противоположного тому, где находиться излучатель.
При v = 2с имеем
.
Волна придет без «красного смещения». Определенная в статье граница возможного приема электромагнитного излучения будет верной, если верен закон Хаббла и «красное смещение» вызвано исключительно удалением излучателя. Если же обнаружатся другие факторы, уменьшающие скорость света относительно приемника (а они могут быть), то граница приема волн может быть приближена.
Обратимся теперь к формулам (1) и (2). В них c-v есть скорость света относительно приёмника, обозначим её с1=с-v откуда v=c-c1.В формулах v представляет разность скоростей света независимо от природы её возникновения. Принято считать, что это результат удаления источника света. Но эта разность скоростей может возникнуть и за счет уменьшения скорости света с увеличением расстояния. Свет это поток квантов энергии и, возможно, что скорость их может уменьшаться.
Предположим, что скорость света с увеличением расстояния от источника света уменьшается, образно говоря «свет стареет».
Известно, что скорость света уменьшается при переходе из оптически менее плотной среды в более плотную. Вызвано это тем, что, что меняются условия для прохождения света. Уменьшение скорости характеризуется показателем преломления n; 
, где с - скорость света в вакууме а с1 - скорость в другой среде.
Если по предположению, скорость света уменьшается с увеличением расстояния от источника света, то, значит, меняются и условия его прохождения, что также можно характеризовать показателем преломления n. Получаем, что уменьшенная скорость света будет 
.
В статье «Опыт Физо» (ж. «Современные наукоёмкие технологии» №2, 2007г.) для определения скорости света в движущейся среде показатель преломления n был использован в виде 
, где 
часть показателя, определяемая излучающим атомом, а 
определяется условиями прохождения света в среде.
Применим такое представление показателя преломления и для вакуума. Если мы приняли предположение, что в вакууме скорость света уменьшается, а вакуум является однородной средой, то уменьшение скорости света должно зависеть только от расстояния и пропорционально ему. Поэтому можно записать 
,где D-расстояние до источника света, μ - коэффициент пропорциональности постоянная величина. Скорость принимаемого света будет
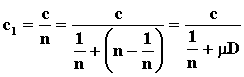
Разность между начальной и уменьшенной скоростями света будет
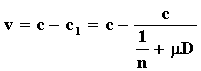
Здесь выражена зависимость между уменьшением скорости света и расстоянием D. Связь между этими же величинами выражает и закон Хабла 
где v- скорость удаления звезды, что для приёмника света есть разность с-с1.
Сравним значения v, которые дают эти два уравнения для предельных значений расстояния D.
Если 
, то из первого уравнения получаем: 
, n=1 (для малых расстояний) 
и 
. Из закона Хаббла также получаем .
Если 
, то из первого уравнения получаем:
Из закона Хаббла получаем
.
Таким образом, для малых расстояний эти уравнения дают одинаковый результат и, значит, для расчетов можно ими пользоваться, как дополняющими друг друга. Воспользуемся этим для определения значения коэффициента пропорциональности μ. Из закона Хаббла находим значение v, например, для
.
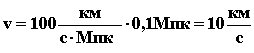И дальше
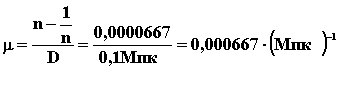
Таким же способом вычислим ещё несколько значений μ. Чтобы не утруждать читателя, приведём результаты для
D равных: 
Получены значения μ соответственно:
; 
; 
; 
; 
.
Получается среднее значение
.
При вычислениях степень точности определялась возможностями микрокалькулятора.
В полученных значениях μ показатель степени десяти зависит от выбора единицы измерения расстояния D. Если за единицу длины взять парсек (пк), то получим
Если за единицу длины взять 0,1пк=1дпк (деципарсек), то получим:
.
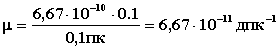Получилось удивительное совпадение: гравитационная постоянная в законе всемирного притяжения равна
Если это совпадение не случайно, можно предположить, что кванты световой энергии связаны с излучателем, на это же указывает и связь светонесущей среды с источником света.
Чтобы определить скорость с1, надо решить относительно n уравнение:
и через n найти скорость с1.
Для малых значений D можно использовать закон Хаббла.
В статье имеется явное противоречие. Основываясь на понятии о расширении Вселенной, получен вывод о существовании границы возможного приема электромагнитных волн, а, основываясь на естественном уменьшении скорости света, такая граница отсутствует. Получается, что обнаружение такой границы будет являться доказательством расширения Вселенной.
В статье также без убедительных оснований принято предположение о зависимости скорости света от расстояний. Основания для этого предположения будут обнаружены при рассмотрении процесса излучения квантов света атомом.
СПИСОК ЛИТЕРАТУРЫ:
- Зисман Г.А., Тодес О.М., Курс общей физики т.3. - М.: «Наука», 1972г.
- Воронцов - Вельяминов Б.А. Астрономия 10. - М.: «Просвещение», 1983г.