Ранее исследованное аналитическое решение линеаризованной задачи в такой постановке свидетельствует о существенной нестационарности истечения газа из пористой среды из-за сопротивления «скелета». Полученные результаты расчета линеаризованной задачи об истечении газа из пористой двухкомпонентной среды при нагрузках протяженного характера позволяют контролировать корректность и точность численного анализа более сложных нелинейных задач этого класса и являются первым шагом алгоритма расчета исследуемой проблемы. Следующим шагом алгоритма в рамках развиваемого подхода является математическое моделирование нелинейной задачи о внешнем воздействии на пористую среду, состоящую из твердого «скелета».
Волновая конфигурация среды имеет вид, показанный на рисунке 1.
При математическом моделировании (величина термина функции U(x,t) - перемещение сечения газа) этого физического процесса и исследовании кинетики и динамики истечения газа из пористой двухкомпонентной среды, вызванного внешним источником воздействия при неполной информативности условий на поверхности объекта воздействия, возникает необходимость адекватного учета ряда особенностей этого процесса:

Рис.1. Волновая конфигурация
1. неполноты набора необходимых данных (из необходимых 8 данных в двух областях):
а) в области 1 - только одно граничное условие на поверхности поршня Ut(0,t) = V0 (означает совпадение скорости частицы газа со скоростью поршня, когда частица находится на поршне); второе граничное условие (деформация частиц газа, находящихся на поршне) Ux(0,t) не задано.
б) в области пористости 1 - заданы только два начальных условия Ux(x,0) =Ut ( x,0)
2. наличия неизвестной подвижной границы l(t) которая разделяет области пористости «чистого» газа, на которой неизвестные функции
U1(l(t),t) = φ 1(t) - со стороны области 1
U2(l(t),t) = φ2(t) - со стороны области 2
должны определяться в процессе расчета на каждом расчетном шаге с обеих сторон подвижной границы, а затем «стыковаться», исходя из условий, полученных (глава 5) на границе областей как условия на скачке:
3. разрыва скорости частиц газа в области пористости в начальный момент процесса, что может приводить к появлению центрированных волн в области пористости вблизи начала координат.
4. возмущения среды в областях 1 и 2 распространяются вдоль соответствующих характеристик, поэтому расчеты в них должны вестись методом характеристик последовательными шагами, обеспечивающими самосогласованное нахождение, как характеристик, так и параметров среды в соответствующих областях.
Математическая модель движения газа в области 1 имеет вид:
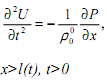
x>l(t), t>0
где давление определяется из уравнения состояния газа в этой области:
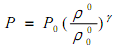
а плотность законом сохранения массы
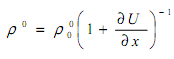
учет которых после ряда преобразований приводит к следующему уравнению для U (x,t) в области 1
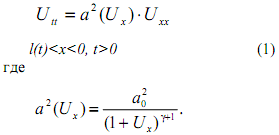
a0 - скорость звука в невозмущенном газе; при одном заданном граничном условии:
Ux(0,t) = V0; второе граничное условие, определяющее деформацию частиц газа на поршне
Ux(0,t) - неизвестная функция, которая определяется на каждом расчетном шаге.
Течение газа в скелете (область 2) моделируется уравнением Х.А. Рахматуллина, соответствующим законом сохранения массы и уравнением состояния газа в пористой среде.
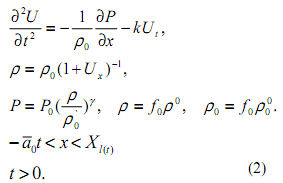
где ρ 0, ρ, P - истинная, приведенная плотности и давление газа, соответственно f0 -пористость скелета среды, ρ 00, ρ 0, P0 - соответствующие значения ρ 0, ρ, P при начальных (нормальных) условиях, к - коэффициент взаимодействия газа со скелетом.
Из приведенной системы для области 2 после ряда преобразований получено следующее уравнение для функции U(x, t)
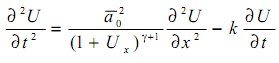
или сокращенно
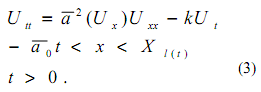
где ![]() - скорость звука в двухкомпонентной среде.
- скорость звука в двухкомпонентной среде.
Член - kU1, выражает взаимодействие частиц газа с частицами скелета, которое моделируется силой Стокса, связанной с относительной скоростью газа, когда характерное число Рейнольдса обтекания частицы скелета невелико (Re ≤1).
Начальные условия модели:
U x =Ut =0 при ![]()
Поскольку передний фронт возмущения в двухкомпонентной пористой среде распространяется со скоростью звука в ней, то начальные условия Ux = Ut = 0 переносятся на характеристику
![]()
что позволяет начать численный расчет с точек, лежащих на ней.
Следуя указанному подходу нами установлено, что в плоскости x,t существует два характеристических направления, имеющих один и тот же вид для областей 1 и 2,
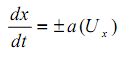
вдоль которых выполняются условия:
для области 1 dUt = ±a(Ux)dUx (6)
для области 2 ![]()
Установлено также, что начало координат является особой точкой, а именно точкой пересечения характеристик и точкой разрыва величин Ux,Ut Приближение к нему вдоль оси Ох, дает
Ux = Ut = 0
а вдоль оси Ot соответственно
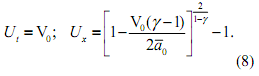
Эти соотношения свидетельствуют о том, что в окрестности начала координат в области пористой двухкомпонентной среды возникают центрированные волны Римана, граница (тангенс угла наклона граничного луча с осью Ot которых определяется по формуле
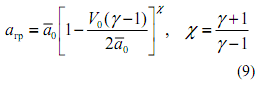
На начальном этапе алгоритма расчета определены характеристики (волны Римана), исходящие из начала координат в области пористости и задан "шаг" ∆L расчетной схемы по углу
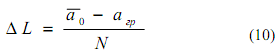
где N - число "шагов".
Шаг по углу в окрестности начала координат, в области 2, где возникают центрированные волны, подобран на основе численного эксперимента.
Из (8) - (10) определены соответствующие этим "шагам" значения Ux,Ut вблизи начала координат (при подходе к началу координат по лучам).
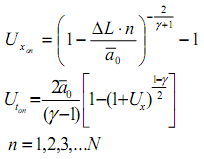
Схема этого этапа численного расчета представлена на рисунке 2.
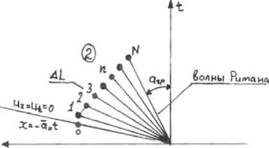
Рис. 2
Используя найденные на начальном этапе параметры среды в области центрированных волн, осуществляется переход к следующему этапу алгоритма расчета в области пористости 2. Волны разряжения распространяются со скоростью звука в двухкомпонентной среде по характеристикам. Область возмущения ограничена фронтом звуковой волны, на которой параметры среды соответствуют параметрам невозмущенной среды и принимаются за начальные на следующем пространственно-временном шаге. Значения параметров на слоях (т = 1,2,3,...) в точках (m,0) известны (начальные значения на ![]() ). Задается шаг ∆t на оси времени и проводится прямая, параллельная оси Ох до пересечения с
). Задается шаг ∆t на оси времени и проводится прямая, параллельная оси Ох до пересечения с ![]() . Получается узел (1,0), из которого проводится положительная характеристика с угловым коэффициентом
. Получается узел (1,0), из которого проводится положительная характеристика с угловым коэффициентом ![]() , выраженным через параметры газа в точке (1,0), до пересечения с лучом ∆L (первого "шага") из начала координат 0. Далее определяется узел (1,1) и т.д. вплоть до (1, N). Алгоритм расчетов представлен по схеме, показанной на рисунке 3.
, выраженным через параметры газа в точке (1,0), до пересечения с лучом ∆L (первого "шага") из начала координат 0. Далее определяется узел (1,1) и т.д. вплоть до (1, N). Алгоритм расчетов представлен по схеме, показанной на рисунке 3.
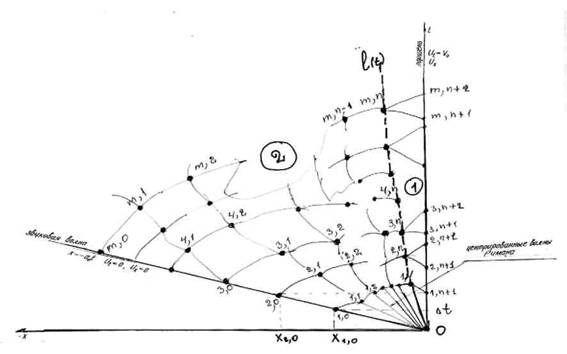
Рис. 3
В соответствии с отмеченной особенностью границы l(t) математическое моделирование условий на границе раздела областей (со слоя т = 2) производится как на ударной волне, то есть на основе соотношений:
После определения параметров Ux,Ut,x,t в узле (т,п) пористой среды, выражается плотность и давление газа в нем по формулам
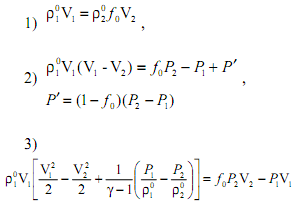
которые дополняются уравнениями состояния газа для пористой области и области «чистого» газа среды
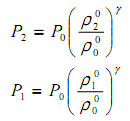
условием для скорости частиц газа на поршне
V1=V0
и условием, выражающим скорость частиц газа в области пористости (так называемым интегралом Римана),
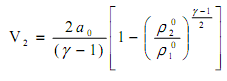
последнее выражение позволяет провести расчеты на начальном этапе без недостающих классических начально-граничных условий, где нижний индекс 2 или 1 означает соответствующий параметр в искомой точке границы l(t) при подходе слева (со стороны области 2 - пористая среда) или справа (со стороны области 1 - чистого "газа").
Пользуясь этими уравнениями в каждой граничной точке l(t) слоя т устанавливается связь параметров V1,V2,ρ10,ρ20,P1,P2 на границе раздела двухкомпонентной пористой среды и чистого "газа".
Затем из граничной точки (m, n) со стороны области I проводятся две характеристики до пересечения с осью Ot и записываются условия вдоль этих характеристик, согласно формулам (5), (6), в виде разностных уравнений
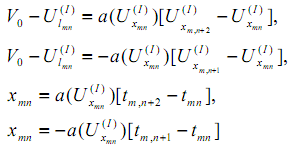
(где верхний индекс означает подход к граничной точке (m,n) со стороны области I -чистого "газа".
Из этих соотношений находятся деформация частиц газа, время в искомых точках (т, n +1); (т, n + 2) на оси времени, (т.е. на поршне). По соответствующим формулам находятся и другие характеристики (Р, р, а) процесса движения газа в области "чистого" газа 1.
По разработанной методике и схеме произведен численный расчет на ЭВМ параметров истечения газа в среде кварц -воздух.
Необходимым условием его устойчивости, как и для разностных схем уравнений газовой динамики, является условие Куранта на шаг интегрирования по времени ∆t,
![]()
где а - местная скорость звука, ∆x.∆t -размеры ячейки в области расчета.
В исследованной начально-граничной задаче, моделирующей внешнее воздействие на объект (пористая двухкомпонентная среда), при недостаточной информативности об этом действии установлено положение границы l(t) раздела пористой среды и газа, определяющей расход газа.
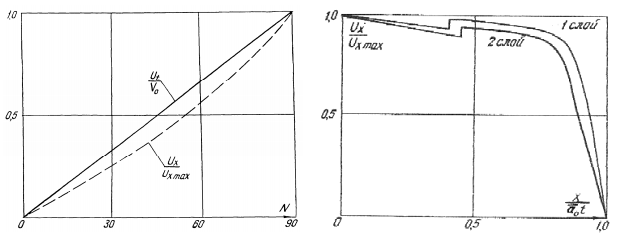
Некоторые результаты численного расчета в виде графиков распределения представлены на рисунках 4-7.
Существенно новые результаты, являющиеся следствием развитого в работе алгоритма математического моделирования сводятся к следующему: в той части среды, которая является пористой, в окрестности начала координат возникают центрированные волны Римана, а истечение газа из двухкомпонентной пористой среды, является значительно нестационарным из-за сопротивления течению газа со стороны скелета.
|
Рис. 4. Распределение скорости и деформации частиц газа, отнесенные к их максимальным значениям в области центрированных волн |
Рис. 5. Кривые распределения скорости и деформации частиц газа по двум рассчитанным слоям в областях 1 и 2 (m = 1, 2) |
|
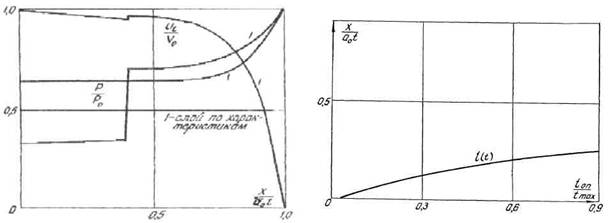
Рис. 6. Кривые распределения давления, плотности, скорости, отнесенные к их максимальным значениям на первом расчетном слое |
Рис. 7. Кривая распределения расхода газа на границе пористости и "чистого" газа |
Новой является также программно-алгоритмическая разработка задачи, которая приложима к решению типовых задач, моделирующих процессы переноса в многофазных, многокомпонентных средах при неполной информации о внешнем воздействии на нее.
СПИСОК ЛИТЕРАТУРЫ:
- Нигматулин Р.И. Динамика многофазных сред. М., Наука, 1987. т.1, 464 с.
- Рахматулин Х.А. Газовая и волновая динамика. М., МГУ, 1983.
- Рахматулин Х.А., Кубанова А.К. Волновое движение трехкомпонентной среды под действием нагрузки, бегущей по плоской границе. Вестник МГУ, сер.1 Математика, механика, 1983, №4, 100-106 с.
- Министерство обороны РФ. Центральный физико-технический институт. Физика ядерного взрыва. М., Наука, 1997. т. 1, 528 с.
- Кубанова А.К., Сагомонян Е.А. Об истечении газа из пористой среды. Вестник Московского университета, сер. 1, Математика, механика, 2004, №4, с. 62-64
- Кубанова А.К. Математическое моделирование волны в двухфазной среде. Вестник Самарской государственной экономической академии, 2002, №1, с. 279-287



