В последнее время появилось большое число работ, посвященных разработкам многослойных нейронных сетей (НС). НС доказали свою эффективность при управлении сложными объектами [5, 6, 9, 10]. Дальнейшие перспективы нейронного управления [10] связаны с указанием параллелей между классической теорией адаптивного управления и подходов к построению нейрорегуляторов (НР) на основе НС. НС являются нелинейными системами, пригодными для решения практических задач управления, принципиально связанных с наличием нелинейных характеристик. НС позволяют устранить количественную неопределенность информации, поскольку после обучения могут за счет интерполяции (эмуляции) и экстраполяции (адаптации и прогнозирования) входо-выходных характеристик физического объекта выдавать верное решение для получения новой информации, не входящей в обучающий набор.
Аналогичную функцию выполняют традиционно используемые адаптивные системы. Адаптивный подход предполагает наличие линейной математической модели, основанной на физических явлениях, и оценку неизвестных параметров, включенных в эту модель.
Основной недостаток НС, организованных по последовательной схеме, - медленная сходимость алгоритмов адаптации (обучения и управления) в реальном времени - существенно ограничивает практическое применение нейронного управления. Существующие схемы нейронного управления оказываются квазиадаптивными с настройкой вне темпа процессов управления либо, будучи, по сути, адаптивными, недостаточно обоснованными из-за сложностей анализа работоспособности, устойчивости, качества и достижения целей управления [7].
Предлагаемый в работе подход к совмещенному синтезу (синтезу в реальном или в ускоренном времени) нейрорегуляторов технологических процессов направлен на преодоление этих сложностей.
1. Постановка задачи нейронного управления
Рассмотрим технологический процесс (ТП), состоящий из l взаимодействующих технологических модулей (ТМ). ТМ имеют общую, известную заранее структуру, и отличаются только переходами от j-го входа к i-му выходу ТП. Полагаем, что каждый ТМ выполняет определенную функцию сложного ТП и описывается последовательным соединением линейной дифференциальной системы (линеаризованной на интервале дискретизации (наблюдения) нелинейной системы обыкновенных дифференциальных уравнений) объекта и нелинейного безынерционного преобразователя (НБП) - однослойного персептрона (искусственного нейрона). Такие ТМ образуют класс абсолютно устойчивых нелинейных систем [2].
Уравнения j-го ТМ (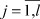 ) имеют вид
) имеют вид
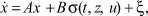 (1)
(1)
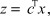 (2)
(2)
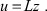 (3)
(3)
Индекс j для краткости записей переменных и параметров системы уравнений (1)-(3) опускаем. В дальнейшем полагаем, что система (1) должна удовлетворять требованиям существования и единственности решения; n-вектор неконтролируемых возмущений 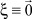 .
.
В формулах (1)-(3) обозначено: 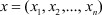 - n-мерный вектор состояния j-го ТМ,
- n-мерный вектор состояния j-го ТМ,  ;
;
u - управление j-м ТМ (измеряемый скалярный вход системы (1)), 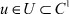 ;
;
z - наблюдение j-м ТМ (измеряемый скалярный выход системы (1)), 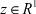 ;
;
A - постоянная параметрически неопределенная матрица Якоби размерности n×n;
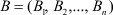 - постоянный вектор настраиваемых параметров НБП размерности n×1;
- постоянный вектор настраиваемых параметров НБП размерности n×1;
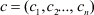 - вектор-столбец задаваемых параметров наблюдения (регрессии) размерности 1×n;
- вектор-столбец задаваемых параметров наблюдения (регрессии) размерности 1×n;
L - скалярный параметрический регулятор;
σ(t, x, z) - скалярная функция активации (ФА) однослойного персептрона, получаемая нелинейным преобразованием j-го управления u и j-го наблюдения z.
Структура однослойной нейронной сети, параметрически адаптированной под j-й ТМ, представлена на рис. 1.
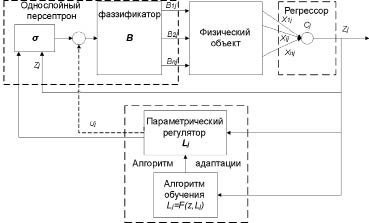
Рис. 1. Структура однослойной нейронной сети, параметрически адаптированной под j-й ТМ
На рис. 1 сплошными линиями обозначена структура однослойной НС с нелинейностью в «прямой цепи» (прототип - структура адаптивного регулятора (рис. 16, а) работы [5, с. 351]). Предлагаемая структура отличается от традиционной схемы адаптивного регулятора (АР) наличием НБП и положительной жесткой обратной связью по скалярному выходу . Данная структура НС добавлена пунктирной линией и сумматором - «цепью внутренней обратной связи» по скалярному входу (прототип - структура адаптивного регулятора (рис. 16, б) работы [5, с. 351]), которой соответствуют модифицированные уравнения (1) j-го ТМ
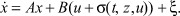 (1*)
(1*)
Дифференциальные уравнения (1*) описывают широкий класс объектов с неопределенностью и позволяют обособить разрывные системы управления в новый класс интеллектуальных систем ассоциативной адаптации [3].
ФА определяет архитектуру НС. Однозначных рекомендаций по выбору ФА в настоящее время не существует. В режиме обучения of-line наиболее эффективен алгоритм обратного распространения ошибки сигнала и следующие ФА: гиперболическая тангенциальная, линейная и логическая сигмоидальная функции активации [6, 9].
В режиме on-line (оперативное обучение и управление), когда НС работает в реальном времени и выполняет функции адаптивного регулятора, будем полагать, что ФА удовлетворяет условиям [1]
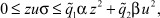 (4)
(4)
где 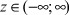 ,
, 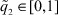 ,
, 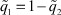 ,
, 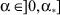 ,
, 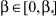 ;
; 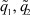 - корректируемые на интервалах наблюдения нечеткие коэффициенты, определяющие перераспределение сигналов от входа к выходу и от выхода к входу (режим работы НС); α, β - весовые коэффициенты соответствующей физической размерности (ед.) при переменных в правой части ограничений на σ.
- корректируемые на интервалах наблюдения нечеткие коэффициенты, определяющие перераспределение сигналов от входа к выходу и от выхода к входу (режим работы НС); α, β - весовые коэффициенты соответствующей физической размерности (ед.) при переменных в правой части ограничений на σ.
Замечание 1. ФА для простоты анализа считаем безынерционной функцией, то есть принимаем 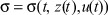 . Она не непрерывна по u и z, имеет разрывы: u = 0, z = 0. Будем считать их изолированными, а ФА в точках разрыва - стационарной:
. Она не непрерывна по u и z, имеет разрывы: u = 0, z = 0. Будем считать их изолированными, а ФА в точках разрыва - стационарной: 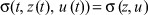 . Решения уравнений (1) в точках разрыва в обычном смысле может не существовать, и под словом «решение» понимается обобщенное решение по А.Ф. Филиппову [5].
. Решения уравнений (1) в точках разрыва в обычном смысле может не существовать, и под словом «решение» понимается обобщенное решение по А.Ф. Филиппову [5].
НБП Bs для j-го ТМ в теории НС и нечетких множеств называется однослойным персептроном с нулевым смещением или фаззификатором, вектор-строка cT - регрессором или дефаззификатором [7]. НБП B(u + σ) (формула (1*)) определяет однослойный персептрон с ненулевым смещением.
При адаптивном подходе считается, что существует устойчивая внутренняя структура физического объекта [5], но неизвестны его параметры (коэффициенты матрицы A). В описании j-го ТМ присутствует и отделима линейная часть с передаточной функцией W(p) (объект) и нелинейность с характеристикой σ(⋅). Поэтому коэффициенты передаточной функции W(p) неизвестны, а относительно нелинейности указаны частичные свойства характеристики σ(⋅). Кроме того, неизвестен вектор B настраиваемых весовых коэффициентов однослойного персептрона.
Требуется осуществить оперативное управление j-м ТМ с помощью адаптивного параметрического нейрорегулятора L.
В основу предлагаемого подхода положена параллель со схемой адаптивного управления с самонастройкой: НС настраивает параметры управления, задающие работу обычного контроллера, таким образом, чтобы выходной сигнал j-го ТМ поддерживался как можно ближе к желаемому: . Такое управление j-м ТМ называется стабилизирующим [5].
Задача синтеза адаптивного параметрического нейрорегулятора решается в три этапа:
1) исследуется выбранный класс нелинейных систем на устойчивость;
2) синтезируется стабилизирующее управление u, обеспечивающее цель адаптации: 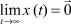 ;
;
3) по условиям устойчивости инициализируются параметры НС.
2. Устойчивость системы
Устойчивость рассматривается как свойство свободного движения системы (1) после начального отклонения ее, вызванного какими-либо причинами. Невозмущенное движение 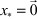 определяется нулевым решением системы (1).
определяется нулевым решением системы (1).
Аналитическое определение понятия устойчивости по Ляпунову формулируется следующим образом [4].
Определение 1. Нулевое решение системы (1) устойчиво, если при заданном сколь угодно малом ε >0 существует такое δ > 0, зависящее от ε, что при начальных условиях 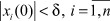 , для решения на интервале 0 < t < ∞ выполняется условие
, для решения на интервале 0 < t < ∞ выполняется условие 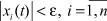 .
.
Если условия определения 1 соблюдены и выполняется условие 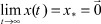 , то нулевое решение системы (1) асимптотически устойчиво. Если условие
, то нулевое решение системы (1) асимптотически устойчиво. Если условие 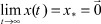 выполняется для любых начальных условий x(0), то нулевое решение системы (1) устойчиво в целом. Асимптотическую устойчивость нулевого решения системы (1) в целом при любом характере нелинейности внутри определенного класса определяет понятие абсолютной устойчивости. На выполнение условия
выполняется для любых начальных условий x(0), то нулевое решение системы (1) устойчиво в целом. Асимптотическую устойчивость нулевого решения системы (1) в целом при любом характере нелинейности внутри определенного класса определяет понятие абсолютной устойчивости. На выполнение условия 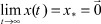 на интервале 0 < t < ∞ налагаются дополнительные требования к характеру переходных процессов внутри трубки
на интервале 0 < t < ∞ налагаются дополнительные требования к характеру переходных процессов внутри трубки 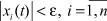 : колебательность, экспоненциальность и др. Будем считать эти процессы экспоненциальными.
: колебательность, экспоненциальность и др. Будем считать эти процессы экспоненциальными.
Определение 2. Нулевое решение системы (1) экспоненциально устойчиво в классе нелинейностей (4), если найдутся константы C и ε > 0, такие, что
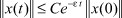
при определенных начальных условиях x(0),  - эвклидова норма (длина) вектора (⋅).
- эвклидова норма (длина) вектора (⋅).
Определение 3. Нулевое решение системы (1) абсолютно экспоненциально устойчиво в классе нелинейностей (4), если найдутся не зависящие от конкретного вида функции s константы C и ε > 0, такие, что
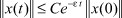
для любых начальных условий x(0),  - эвклидова норма (длина) вектора (⋅).
- эвклидова норма (длина) вектора (⋅).
По аналогии с работой [1] выдвинем следующие гипотезы.
Гипотеза 1. Для абсолютной устойчивости нулевого решения системы (1)-(3) в классе нелинейностей (4) необходимо и достаточно, чтобы эта система была асимптотически устойчива при
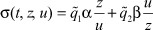
для любых 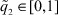 ,
, 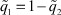 ,
, 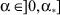 ,
, 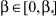 .
.
Гипотеза 2. Для достижения цели адаптации 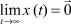 дифференциальной системы (1) необходимо и достаточно, чтобы ее нулевое решение было устойчиво в классе нелинейностей (4).
дифференциальной системы (1) необходимо и достаточно, чтобы ее нулевое решение было устойчиво в классе нелинейностей (4).
Нетрудно видеть, что устойчивость в целом системы (1) предполагает достижение цели адаптации и наоборот. Допущение 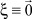 позволяет говорить об абсолютной, а не об асимптотической устойчивости нулевого решения системы (1).
позволяет говорить об абсолютной, а не об асимптотической устойчивости нулевого решения системы (1).
В работе [2] показано, что гипотезам, близким к сформулированным, удовлетворяет система любого порядка, если ее импульсная функция положительна. Тогда задача данного класса абсолютно устойчивых систем сводится к определению эффективных критериев положительности таких функций.
Передаточная функция (ПФ) линейной части системы (1)-(3) от входа σ к выходу z (см. рис. 1) равна
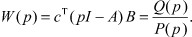
Здесь I - единичная матрица размера n×n;
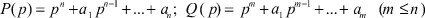 - полиномы для определения полюсов и нулей ПФ W(p).
- полиномы для определения полюсов и нулей ПФ W(p).
Обозначим через p1, ..., pn корни характеристического полинома P(p) (полюса ПФ), а через g(t) - импульсную (весовую) функцию
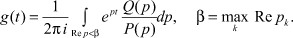 (5)
(5)
Теорема 1. Если при неотрицательной импульсной функции (g(t) ≥ 0 при t ≥ 0) нулевое решение системы (1)-(3) устойчиво в целом, то для достижения цели адаптации 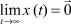 необходимо и достаточно выполнение одного из двух условий в классе нелинейностей (4):
необходимо и достаточно выполнение одного из двух условий в классе нелинейностей (4):
а) матрица A должна быть гурвицевой (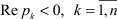 );
);
б) нулевое решение должно быть устойчивым
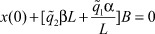
или
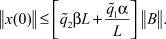 (6)
(6)
Доказательство теоремы. Необходимость условий теоремы показана выше. Докажем теперь достаточность этих условий.
Решение системы (1) запишем в интегральной форме Коши
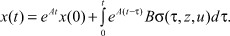
Отсюда следует, что доступный наблюдению сигнал равен
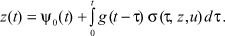
В последней формуле обозначены: 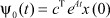 - реакция системы (1)-(3) на начальные условия x(0);
- реакция системы (1)-(3) на начальные условия x(0);
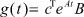 (7)
(7)
- импульсная (весовая) функция системы (1)-(3).
ФА δ(⋅) выписывается с учетом правой части ограничений (4)
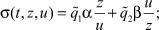
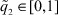 ,
, 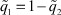 . (8)
. (8)
Тогда, учитывая неотрицательность импульсной функции и неравенства (4), имеем:
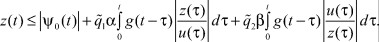
По свойству интегрального оператора в заданном классе функций [2] можно утверждать, что 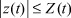 , где Z(t) - решение уравнения
, где Z(t) - решение уравнения
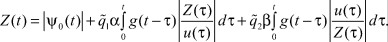
Применим преобразование Лапласа для функций Z(t), 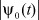 соответственно
соответственно
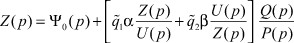
или
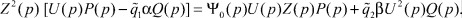 (9)
(9)
В операторном уравнении (9) зависимость наблюдения от параметров линейной части и управления системы (1)-(3) в общем случае довольно сложная. Однако формула (9) существенно упростится, если принять во внимание уравнение регулятора (3)
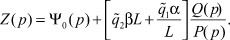 (10)
(10)
Переходя в формуле (10) от изображений к оригиналам функций z(t), ψ0(t) с учетом выражения для импульсной функции (7), получим:
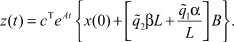 (11)
(11)
Из сравнения формул (2) и (11) находим аналитическое выражение для вектора состояния j-го ТМ
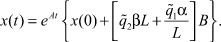 (12)
(12)
Анализ решения (12) системы (1) - (3) показывает, что достижение цели адаптации 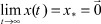 достигается, если выполняются условия а) или б) теоремы. Теорема доказана.
достигается, если выполняются условия а) или б) теоремы. Теорема доказана.
Теорема 2. Если при неотрицательной импульсной функции (g(t) ≥ 0 при t ≥ 0) матрица 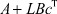 гурвицева и корни характеристического полинома управления имеют особенности в левой полуплоскости, то нулевое решение уравнений (1*), (2), (3) абсолютно экспоненциально устойчиво в классе нелинейностей (4). И, наоборот, если g(t) ≥ 0 при t ≥ 0, нулевое решение уравнений (1*), (2), (3) экспоненциально устойчиво, то матрица A гурвицева, если гурвицев полином U(p) управления u.
гурвицева и корни характеристического полинома управления имеют особенности в левой полуплоскости, то нулевое решение уравнений (1*), (2), (3) абсолютно экспоненциально устойчиво в классе нелинейностей (4). И, наоборот, если g(t) ≥ 0 при t ≥ 0, нулевое решение уравнений (1*), (2), (3) экспоненциально устойчиво, то матрица A гурвицева, если гурвицев полином U(p) управления u.
Доказательство теоремы 2. Решение уравнений (1*) в интегральной форме Коши имеет вид
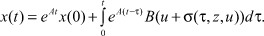
Тогда выходной сигнал z равен
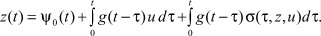
Аналогично доказательству теоремы 1, учитывая неотрицательность импульсной функции и неравенства (4), получим:
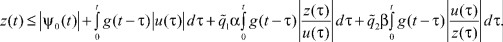 (13)
(13)
Решение уравнения, представленного правой частью неравенства (13), записывается в виде
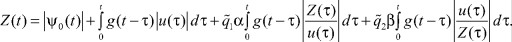 (14)
(14)
Через преобразование Лапласа для функций Z(t), 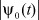 получим:
получим:
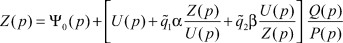
Последняя формула с учетом уравнения регулятора (3) принимает вид
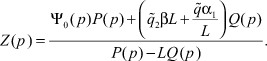 (15)
(15)
Переходя от изображений к оригиналам функций в формуле (15), имеем:
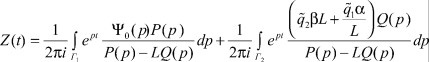
Интеграл по контуру Г1 идентичен интегралу по контуру Г в теореме [2], где доказано, что особенности изображения свободной составляющей решения - реакции системы (1*), (2), (3) на начальные условия ψ0(p) и передаточной функции 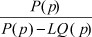 лежат в левой полуплоскости.
лежат в левой полуплоскости.
Покажем теперь, что интеграл по контуру Г2 оставляет слева все особенности подынтегральной функции, а полином P(p) - LQ(p) соответствует замкнутой параметрическим регулятором L системе (1*).
Для этого убедимся, что
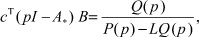
где 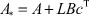 - гурвицева матрица системы (1*), замкнутой традиционным АР, I - единичная матрица размера n×n.
- гурвицева матрица системы (1*), замкнутой традиционным АР, I - единичная матрица размера n×n.
Воспользуемся известным из теории матриц [5] тождеством
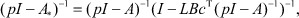 (16)
(16)
которое справедливо при 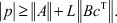
При указанных p сходится ряд
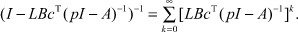 (17)
(17)
Из формул (16), (17) имеем:
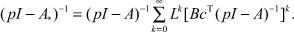 (18)
(18)
Из выражения (18) выпишем передаточную функцию k + 1 члена ряда
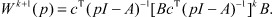 (19)
(19)
Тогда из формул (18), (19) следует:
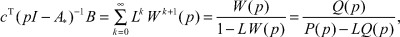 (20)
(20)
что и требовалось показать.
Так как A* - гурвицева матрица, то и полином P(p) - LQ(p) замкнутой параметрическим регулятором L системы (1*) гурвицев.
Таким образом, для того чтобы ФА u + σ(t, z, u) доставляла асимптотическую устойчивость системе (1*), достаточно, чтобы полином U(p) управления u в классе нелинейностей (4) был гурвицевым. Теорема доказана.
Следствие теоремы 2. Для достижения цели адаптации 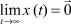 в системе (1*), (2), (3) необходимо и достаточно выполнение одного из двух условий в классе нелинейностей u + σ(t, z, u):
в системе (1*), (2), (3) необходимо и достаточно выполнение одного из двух условий в классе нелинейностей u + σ(t, z, u):
а) матрица 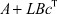 должна быть гурвицевой;
должна быть гурвицевой;
б) условие устойчивости нулевого решения должно совпадать с условием устойчивости нулевого решения уравнений (1)-(3) теоремы 1.
Действительно, из сравнения формул (10), (15), (20) можно заключить, что при переходе к оригиналам в выражении (15) аналитическое решение системы (1*), (2), (3) при ограничениях вида (4) имеет вид
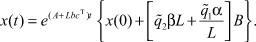 (21)
(21)
3. Настройка нейронной сети по функции активации
Для синтеза стабилизирующего управления в режиме on-line наибольший интерес представляет выполнение условия б) теоремы 1 или следствия теоремы 2 - условия устойчивости нулевого решения, поскольку условие гурвицевости матриц A или известной структуры, но с неизвестными коэффициентами, вносит параметрическую неопределенность в решение задачи построения нейронного регулятора. В режиме of-line условие а) разрешимо, но с привлечением дополнительных, достаточно трудоемких в вычислительном плане процедур параметрической идентификации или робастной стабилизации, построенных на основе матричных уравнений или неравенств Ляпунова [5].
Поэтому более подробно выясним, какой физический смысл имеют задаваемая формулой (8) функция активации и условие б) теоремы.
Нетрудно заметить, что ФА (8) содержит два слагаемых: первое слагаемое соответствует обратному (инверсному) распространению сигнала, второе слагаемое - его прямому распространению.
Так как наблюдение z и управление u в архитектуре встроенной в обычный адаптивный регулятор однослойной НС - скалярные функции, а особые точки считаются изолированными, то ФА (8) для j-го ТМ равна
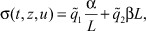
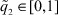 ,
, 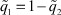 . (22)
. (22)
Зависимость σ(⋅) = σ(L) при фиксированных 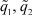 представлена на рис. 2.
представлена на рис. 2.
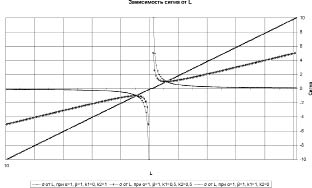
Рис. 2. Зависимость функции активации от значений регулируемого параметра при различных 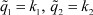 и α = 1 (ед.), β = 1 (ед.)
и α = 1 (ед.), β = 1 (ед.)
В задачах управления параметр 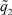 рекомендуется связывать с интервалом наблюдения выходного сигнала z, который разбивается на s периодов дискретизации T0:
рекомендуется связывать с интервалом наблюдения выходного сигнала z, который разбивается на s периодов дискретизации T0: 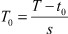 . В каждый период дискретизации выполняется несколько обучающих итераций. В самом простом случае можно принять период дискретизации равным периоду корректировки обучающей итерации: T0 = TL и связать при t0 = 0 период наблюдения выходного сигнала с реальным временем:
. В каждый период дискретизации выполняется несколько обучающих итераций. В самом простом случае можно принять период дискретизации равным периоду корректировки обучающей итерации: T0 = TL и связать при t0 = 0 период наблюдения выходного сигнала с реальным временем:
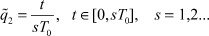
Простой анализ выражений (8), (22) показывает, что нейронная сеть функционирует в трех режимах:
А. Если 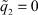 , то выполняется инициализация параметров НС; сеть предварительно обучается (
, то выполняется инициализация параметров НС; сеть предварительно обучается (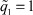 ) по алгоритму обратного распространения ошибки сигнала (в нашем случае сигнала z (z* = 0).
) по алгоритму обратного распространения ошибки сигнала (в нашем случае сигнала z (z* = 0).
Б. Если параметр 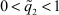 , то в реальном времени происходит дальнейшее обучение нейронной сети и одновременно нейро-нечеткое управление параметрически неопределенного физического объекта известной структуры
, то в реальном времени происходит дальнейшее обучение нейронной сети и одновременно нейро-нечеткое управление параметрически неопределенного физического объекта известной структуры
(см. рис. 1).
В. Если параметр 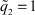 , то процесс обучения сети заканчивается, и НС работает как обычный адаптивный регулятор (
, то процесс обучения сети заканчивается, и НС работает как обычный адаптивный регулятор (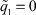 ).
).
Условия А-В представляют собой систему продукционных правил (продукций) и реализуются в блоке принятия решений децентрализованного управления технологической системой с нечеткой структурой взаимосвязей [3].
4. Параметрический синтез стабилизирующего управления методом скоростного градиента
Подстройка НС под эталонную модель (желаемый выходной сигнал) j-го ТМ может осуществляться различными градиентными методами: аналитического конструирования, обратных задач динамики, синергетической теории управления, теории инвариантности, традиционного адаптивного управления. В качестве эффективного алгоритма обратного распространения в статье предлагается использовать метод скоростного градиента (МСГ) [3].
Замечание 2. МСГ был предложен А.А. Красовским [5]. Доказательство общих схем алгоритмов управления по МСГ выполнено А.Л. Фрадковым[8]. МСГ, по существу, является градиентным методом наискорейшего спуска в пространстве параметров.
Формулировка задачи синтеза стабилизирующего управления по МСГ сводится к следующему.
Состояние j-го ТМ -  , управление u - скалярное, наблюдается скалярная величина
, управление u - скалярное, наблюдается скалярная величина 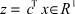 . Эволюцию j-го ТМ описывает дифференциальная система (1*), где измеряемая кусочно-дифференцируемая функция σ(t, z, u) является аддитивной добавкой к скалярному управлению u и подчинена ограничению вида (4), B - постоянный n-вектор настраиваемых входных параметров. Управление линейно зависит от наблюдаемой величины: u = Lz.
. Эволюцию j-го ТМ описывает дифференциальная система (1*), где измеряемая кусочно-дифференцируемая функция σ(t, z, u) является аддитивной добавкой к скалярному управлению u и подчинена ограничению вида (4), B - постоянный n-вектор настраиваемых входных параметров. Управление линейно зависит от наблюдаемой величины: u = Lz.
Матрица A и вектор B заранее неизвестны. Вектор c, учитывающий «вклады» переменных состояния x в наблюдение z, задается.
Требуется синтезировать параметрический регулятор L = L(t).
Цель управления - выполнение условия 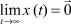 - соответствует минимизации в пределе локального функционала
- соответствует минимизации в пределе локального функционала 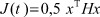 , где H - положительно определенная, симметрическая матрица размерности n×n.
, где H - положительно определенная, симметрическая матрица размерности n×n.
Для синтеза нелинейного параметрического регулятора применим схему МСГ в дифференциальной форме [8].
Для этого определим полную производную от локального функционала
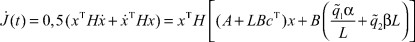
и вычислим градиент по параметру L
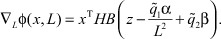
По схеме МСГ синтезируемый в дифференциальной форме нелинейный скалярный регулятор имеет вид:
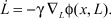 (23)
(23)
Для системы (1*), (2), (3) при ограничениях на ФА типа (4) алгоритм адаптации (обучения) j-го ТМ записывается в виде
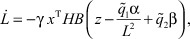 (24)
(24)
где γ > 0 - положительное число, определяющее скорость убывания градиента по параметру L.
По постановке задачи процедура управления должна зависеть только от наблюдаемой величины z (см. рис. 1). Поэтому в (24) потребуем соблюдения равенства
HB = c. (25)
Тогда с учетом того, что 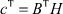 , в окончательном виде получим алгоритм адаптации j-го ТМ
, в окончательном виде получим алгоритм адаптации j-го ТМ
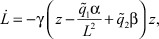 (26)
(26)
где 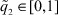 ,
, 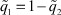 - параметры, определяющие режим работы НС.
- параметры, определяющие режим работы НС.
5. Инициализация начальных условий
Реализация условия устойчивости нулевого решения уравнений j-го ТМ (условие б) теоремы 1 или следствия теоремы 2) для достижения цели адаптации 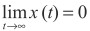 сводится к инициализации начальных условий алгоритма адаптации (26).
сводится к инициализации начальных условий алгоритма адаптации (26).
Воспользуемся равенством (25). Матрицу H в локальном функционале J и в формуле (25) рекомендуется выбирать таким образом, чтобы выполнялось неравенство [5, с. 331]
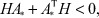 (27)
(27)
где 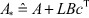 - задаваемая при некотором c = c* , желаемая гурвицева матрица замкнутой регулятором L системы (1*), (2), (3). Матрица A* может быть предварительно идентифицирована (эмулирована в НС) по экспериментальным данным вход-выходных характеристик замкнутого линейным регулятором физического объекта.
- задаваемая при некотором c = c* , желаемая гурвицева матрица замкнутой регулятором L системы (1*), (2), (3). Матрица A* может быть предварительно идентифицирована (эмулирована в НС) по экспериментальным данным вход-выходных характеристик замкнутого линейным регулятором физического объекта.
Неравенство (27) соответствует второй лемме Ляпунова об устойчивости движения и указывает класс технических систем, который алгоритмом адаптации приводится к цели. Этот класс полностью определяется через параметры алгоритма.
Инициализация начальных условий алгоритма адаптации (26) сводится к следующему.
1. Используя пакет Mat Lab Toolbox LMI, методом линейного программирования решаем систему матричных неравенств Ляпунова (27) и определяем матрицу H.
2. Задаваясь весами c = c* выходных сигналов 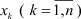 , из формулы (25) вычисляем параметры вектора B НБП:
, из формулы (25) вычисляем параметры вектора B НБП: 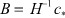 .
.
3. Применяя условие устойчивости б) теоремы 1, определяем начальное условие L(0) алгоритма адаптации (26) 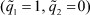 :
:
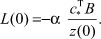
В последующем начальные условия алгоритма адаптации (26) уточняются в реальном времени с шагом, равным периоду дискретизации (интервалу наблюдения) выходного сигнала z.
Альтернативный путь предварительной инициализации параметров НС по алгоритму обратного распространения - использование пакета Neural Toolbox среды Mat Lab.
Дальнейшее оперативное обучение и управление j-м ТМ производится по алгоритму адаптации (26) 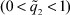 . При
. При 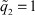 процесс обучения НС заканчивается и НС работает как обычный АР.
процесс обучения НС заканчивается и НС работает как обычный АР.
Заключение
Таким образом, в статье на основе организации параметрического управления по методу скоростного градиента разработан эффективный алгоритм адаптации, позволяющий:
1) ускорить сходимость нейро-нечеткого управления за счет обучения нейронной сети в реальном времени;
2) применить гибридные сети, в которых искусственные нейронные сети связываются со структурами адаптивного управления на основе традиционных технологий;
3) осуществить предварительное обучение и применить эффективные процедуры инициализации параметров нейронной сети.
Для практической реализации алгоритма адаптации на базе однослойной нейронной сети достаточно знаний о порядке дифференциальных уравнений, описывающих физический объект с устойчивой структурой взаимосвязей между ее элементами.
Список литературы
-
Айзерман М.А. О сходимости процесса регулирования после больших начальных отклонений // А и Т. - 1946. - № 2-3. - С. 148-167.
-
Гиль М.И. Об одном классе абсолютно устойчивых систем // А и Т. - 1983. - № 10. - С. 27-36.
-
Пашков Н.Н., Мухопад Ю.Ф., Пунсык-Намжилов Д.Ц. Ассоциативный автомат децентрализованного адаптивного управления системой автономных вычислительных процессов // Научный вестник НГТУ. - Новосибирск: НГТУ, 2009. - № 2 (35). - С. 201-206.
-
Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. - М.: Наука, 1988. - 256 с.
-
Срагович В.Г Адаптивное управление. - М.: Наука, 1981. - 384 с.
-
Управление в условиях неопределенности / под ред. проф. А.Е. Городецкого. - СПб.: Изд-во СПб ГТУ, 2002. - 398 с.
-
Терехов В.А., Ефимов Д.В., Тюкин И.Ю. Нейросетевые системы управления // Нейроконтроллеры и их применение / под ред. А.И. Галушкина. - М.: ИПРЖР, 2002. - 480 с.
-
Фрадков А.Л. Схема скоростного градиента и ее применение в задачах адаптивного управления // А и Т. - 1979. - № 9. - С. 90-101.
-
Омату С., Халид М., Юсоф Р. Нейроуправление и его приложения. Кн. 2 // Нейроконтроллеры и их применение / под ред. А.И. Галушкина, В.А. Птичкина. - М.: ИПРЖР, 2000. - 272 с.
-
Hunt K.J., Sbarbaro D., Zbikowski R., Gawthrop P.J. Neural Network for Control Systems - a Survey // Automatica. - 1992. - Vol. 28. - P. 1083-1112.
Рецензенты:
Данеев А.В., д.т.н., профессор, ФГОУ ВПО «Восточно-Сибирский институт МВД России», г. Иркутск;
Дунаев М.П., д.т.н., профессор, Иркутский государственный технический университет, г. Иркутск.



